Funksjon (matematikk)
| Områder i algebra |
| Abstrakt algebra |
| Algebraisk geometri |
| Elementær algebra |
| Kombinatorikk |
| Lineær algebra |
| Tallære |

I matematikk er en funksjon en relasjon mellom to mengder, slik at det til ethvert element i den første mengden (funksjonsargument, uavhengig variabel, -verdi) blir tilordnet ett element i den andre mengden (funksjonsverdi, avhengig variabel, -verdi). Et eksempel på en slik relasjon er som viser forholdet mellom argumentet og kvadratet av dette og som leses «f av x er lik x i andre». Presentasjonen av en formell definisjon av en funksjon varierer i litteraturen.
Funksjonsbegrepet er svært sentralt i moderne matematikk og inngår også som en viktig del av matematikkundervisningen i skolen.
En funksjon kan spesifiseres på mange forskjellige måter: som en formel, som en graf, ved å beskrive egenskapene eller ved å spesifisere en algoritme for funksjonsverdiene. Funksjonen kan også defineres ved å beskrive forholdet til en annen funksjon, for eksempel som en invers funksjon eller som en sum av to funksjoner.
Som en følge av at funksjonsbegrepet er så viktig i matematikk, eksisterer det en stor og rik terminologi knyttet til dette. Begrepene avbildning, operator, transformasjon og det engelske mapping brukes av og til synonymt med «funksjon», av og til med en tillagt nyanse i forhold til denne. Ofte brukes begrepene operator, transformasjon og mapping spesielt for funksjoner der både argumentmengden og verdiområdet er abstrakte rom, slik som for en lineær transformasjon. Operator brukes ofte for å betegne en funksjon der definisjonsmengden består av funksjoner.
Historie[rediger | rediger kilde]

Relasjoner mellom to typer størrelser dukker tidlig opp i matematisk historie, selv om det skulle gå lang tid før slike relasjoner ble eksplisitt omtalt som en «regel» eller enda mer presist, som en «funksjon». Telling som grunnleggende operasjon er en form for funksjon, med en relasjon mellom abstrakte tall og et sett av objekter. Fra oldtidens Mesopotamia har vi tabeller med relasjoner mellom tall og inverser, kvadrattall og kubikktall.[1] Utarbeiding av forskjellige former for matematiske tabeller har vært viktig helt siden oldtiden og fram til dagens almanakker, ikke minst motivert ut fra astronomi. De første formene for tabulering av trigonometriske relasjoner finner vi i gresk matematikk fra før Kristi fødsel.[2] Tabulering av matematiske funksjoner fortsatte helt til utviklingen av datamaskiner gjorde slike tabeller overflødige, og Mathematical Tables Project ble avviklet i 1948. Dette prosjektet hadde resultert i utgivelsen av standardverket Handbook of Mathematical Functions, der siste utgave kom i 1972.[3]
En annen viktig inspirasjonskilde som sakte og gradvis ledet opp til introduksjonen av funksjoner, var studiet av kurver, et studium som også har røtter i gresk matematikk. Det skulle likevel gå svært lang tid fra gresk matematikk til de første forsøkene på en formalisering av funksjoner fant sted. Nicole Oresme (1323?-1382) introduserte idéen om at en relasjon mellom målbare fysiske størrelser kan visualiseres som en plan figur, som vi i dag ville kalle grafen til en funksjon.[4] René Descartes (1596-1650) og Pierre de Fermat (1601-1665) la grunnlaget for analytisk geometri og dermed sammenhengen mellom koordinater og kurver. Descartes påpekte at en ligning i to variable, representert ved en kurve, vil definere en relasjon mellom de to størrelsene. Fermat ga ligninger for kjeglesnittene, og drøftet også metoder for å finne maksimum til en «kvantitet», som var ett av ordene brukt for å omtale det vi i dag vil kalle en funksjon.
Studiet av kurver var en viktig motivasjon for differensial- og integralregning, utviklet omtrent samtidig og uavhengig av hverandre av Isaac Newton (1642-1726) og Gottfried Leibniz (1646-1716). Newton brukte symbolet for å betegne den deriverte av en størrelse . Leibniz var den første til å bruke ordet «funksjon», i 1694.[5][6] Ordet ble konstruert fra «functus», som er perfuktum partisipp av det latinske verbet «fungi», med betydning «å utføre». Leibniz introduserte også begrepene «variabel», «parameter» og «konstant».
En funksjon ble av Leibniz skrevet som en enkelt gresk bokstav eller ved hjelp av symbol[7]
Leonhard Euler (1707-1783) var den første, i 1734, som skrev en funksjon som , der bruken av bokstaven var inspirert av ordet funksjon.[7][6]. For en funksjon av to variable brukte brukte Euler senere flere ganger en notasjon med et ekstra kolon, som i .
Joseph Louis Lagrange (1736-1813) bidro med verket Theorie des fonctions analytiques (Paris, 1797) sterkt til å klargjøre funksjonsbegrepet og også til videre bruk av funksjonssymbolet .[7] Verket introduserer også notasjonen for den deriverte av funksjonen.[8]
Differensial- og integralregningen skapte interesse både for kurver og funksjoner, ut over de tradisjonelle kjeglesnittene og de rasjonale funksjonene. Rasjonale funksjoner er funksjoner som kan uttrykkes som brøker av polynom. Selv integralet av en enkel funksjon som krever bruk av transcendente funksjoner, funksjoner som ikke kan uttrykkes ved hjelp av polynomuttrykk. Betafunksjonen og gammafunksjonen er to slike transcendente funksjoner, begge introdusert av Euler. Navnene og symbolene for disse to funksjonene ble først etablert mange år senere. Niels Henrik Abel (1802-1829) har sammen med Carl Gustav Jacobi (1804-1851) og Carl Friedrich Gauss (1777-1855) fått æren av å ha introdusert elliptiske funksjoner, en generalisering av trigonometriske funksjoner.[9]
Viktig for bruken av stringens og presisjon i matematisk analyse for funksjoner var arbeidet til Augustin Louis Cauchy (1789-1857). Cauchy er kanskje mest kjent for å etablere kompleks funksjonsteori, det vil si studiet av funksjoner der både argument og funksjonsverdi er komplekse tall. Arbeidet til Cauchy ble videreført av blant andre Pierre Alphonse Laurent (1813-1854) og Bernhard Riemann (1826-1866). Den førstnevnte oppdaget hvordan komplekse funksjoner kan utvikles i uendelige potensrekker, det som i dag kalles Laurent-rekker.
I analysen til Leibniz og Newton er funksjonene reelle og kontinuerlige deriverbare størrelser. Det hadde lenge vært velkjent at slike funksjoner under nokså generelle vilkår kan utvikles i potensrekker eller Taylorrekker, og funksjoner som oppfyller slike vilkår kalles analytiske. Joseph Fourier (1768-1830) antok at alle funksjoner også kan utvikles i rekker av trigonometriske funksjoner, det vi i dag kaller fourierrekker. For å kunne utvikles i en fourierrekke trenger funksjonen ikke å være kontinuerlig, den kan ha periodiske diskontinuiteter. I første halvdel av det attende århundre begynte matematikere å trekke fram flere funksjoner som brøt med den tradisjonelle forestillingen til Leibniz og Newton: Bernhard Bolzano (1781-1848) publiserte i 1834 et eksempel på en kontinuerlig funksjon som ikke er deriverbar i noe punkt.[10] Peter Gustav Dirichlet (1805-1859) ga et eksempel på en funksjon som ikke er kontinuerlig i noe punkt: Funksjonen har verdien for rasjonale argument og verdien for irrasjonale argument. Denne funksjonen kalles nå Dirichlets funksjon. Bernhard Riemann ga et eksempel på en funksjon som er diskontinuerlig i uendelig mange punkt, men likevel integrerbar.
Erkjennelsen av det eksisterte «patologiske» funksjoner førte til en løsrivelse av begrepet «funksjon» fra det geometriske begrepet «kurve». I 1837 definerte Dirichlet en funksjon som «en relasjon mellom to variable og , slik at til en hver numerisk verdi tilordnet , så er det en regel som også tilordner en entydig verdi av ». Denne definisjonen nærmer seg den moderne formen.[11] Løsrivelsen fra geometri var ledd i et større program for å frigjøre matematisk analyse fra geometri, et program der Karl Weierstrass (1815-1897) var en viktig skikkelse. I dette arbeidet var sammenhengen mellom uendelige rekker og funksjoner sentralt.
I løpet av attenhundretallet ble det gradvis innført mer stringens og presisjon i matematisk analyse og i algebra. Samtidig skjedde det en utvikling der matematikken ble mer og mer abstrakt. Som ledd i arbeidet med å etablere en stringent basis for algebra, påpekte George Peacock (1791-1858) i 1834 at elementene som bokstavene og symbolene refererte til, ikke trengte være tall. Disse elementene kunne være hva som helst, så lenge de oppfylle spesifiserte matematisk krav. Mengdelæren innført av Georg Cantor (1845-1918) ble et viktig grunnlag for abstraksjonsprosessen også for funksjoner, der funksjoner ikke lenger trengte være knyttet til tall. Engelske matematikere var spesielt interessert i forbindelsen mellom matematikk og logikk, matematisk logikk. Augustus De Morgan (1806-1871) og Charles Peirce (1839-1914) var begge viktige for å sette i gang et formelt studium av relasjoner, basert på mengdelæren.
I 1908 definerte Godfrey Harold Hardy (1877-1947) en funksjon som en relasjon mellom to variabler og , der det «til noen verdier av alltid korresponderer verdier av ».[12] Hardy krevde ikke at funksjonen skulle være definert for alle verdier av og heller ikke at funksjonen skulle forbinde en verdi av til en enkelt, entydig verdi av . Denne brede definisjonen av en funksjon omfatter flere relasjoner enn det den vanlige, samtidige matematikken betraktet.[trenger referanse]
Giuseppe Peano (1858-1932) introduserte i 1888 vektorrom, og den aksiomatiske teorien ble i de første tiårene av 1900-tallet videreutviklet av David Hilbert (1862-1943) og Stefan Banach (1892-1945).[13] I 1908 beskrev Maurice René Fréchet (1878-1973) i doktorarbeidet sitt metriske rom, og han var den første som brukte betegnelsen «rom» om abstrakte matematiske strukturer. Både metriske rom og vektorrom har blitt fundamentalt viktige i funksjonsstudier, ved å knytte abstrakte geometriske egenskaper svarende til lengde og avstand også til funksjoner. En rekke spesielle funksjonsrom er senere blitt definert og studert. Fréchet introduserte i doktorarbeidet også funksjonaler, en spesiell klasse av funksjoner som har reelle eller komplekse tall som verdiområde.[14][15]
Den engelske fysikeren Paul Dirac (1902-1984) innførte funksjonen som nå kalles Diracs deltafunksjon, til hjelp i kvantefysikk, et eksempel på at «patologiske» funksjoner kan være til nytte i beskrivelse av fysiske fenomen. Deltafunksjonen tilhører en klasse av generalisert funksjoner, også kalt distribusjoner, der teorien ble utviklet av Sergei Sobolev (1908-1989) og Laurent Schwartz (1915-2002).[trenger referanse]
Formell definisjon[rediger | rediger kilde]

En intuitiv idé om en funksjon som en «regel» er svært gammel og er fremdeles brukt som definisjon i en del lærebøker i matematisk analyse. En funksjon defineres da som en regel som tildeler hvert element i en mengde D ett enkelt element av en mengde C.[16] Selv om definisjonen er tilstrekkelig for mange formål, er det ikke alltid tilfredsstillende at den støtter seg på det udefinerte begrepet «regel».
I dag er det vanlig å tolke «regel» som en binær relasjon. Formelt kan en funksjon fra en mengde til en mengde defineres som en mengde av ordnede par i det kartesiske produktet . Mengden skal være entydig, i den forstand at hvis og , så er .[16][17][18][19]
Definisjonen krever ikke at er definert for alle elementer i mengden . Dersom funksjonen er definert for alle elementer i , så sies funksjone å være total.[trenger referanse] Vanligvis blir ordet funksjon brukt til å bety en total funksjon. Ikke-totale funksjoner er viktige i funksjonsanalyse, matematisk logikk og kategoriteori.
Mengden kalles grafen til funksjonen. Ikke alle forfattere skiller mellom funksjonen og grafen,[17] og denne identifikasjonen fjerner behovet for spesifisere og i den formelle definisjonen.
Definisjonsmengden til funksjonen er mengden av alle elementer som funksjonen er definert for:
Synonyme ord er definisjonsområde, domene og kilde. Et element i definisjonsmengden er et argument for funksjonen. For en total funksjon er .
Mengden C kalles verdiområdet til funksjonen. Mengden av elementer i som svarer til et ordnet par i , kalles verdimengden til :
Verdimengden er en delmengde av verdiområdet. Alternative navn for verdiområdet er kodomenet og for verdimengden bildet eller bildemengden.
Nullmengden til en funksjon er mengden av argument som gjør funksjonen lik null. . Nullmengden er en delmengde av definisjonsmengden.
Ulike disipliner kan bruke spesielt tilpassede varianter av den formelle funksjonsdefinisjonen. I kategoriteori blir i noen sammenhenger mengden D kalt definisjonsmengden til f, selv om funksjonen f ikke er definert for hvert element i D.[trenger referanse] I andre disipliner kan en droppe kravet om at en funksjon skal være entydig, det vil si returnere kun én verdi for et gitt argument.[6][20] En bruker da formuleringer som en «entydig funksjon» og en «flertydig funksjon» for å skille mellom disse to tilfellene.
Notasjon[rediger | rediger kilde]
I stedet for en notasjon basert på ordnede par er det også vanlig å skrive funksjonen som . Vanligvis brukes en enkelt bokstav, som , i kursiv skrift. Både små og store bokstaver blir brukt. For en del standard funksjoner brukes flere bokstaver, for eksempel for trigonometriske funksjoner. For slike standardfunksjoner dropper en også gjerne parentesene, dersom det ikke er fare for misforståelser, slik som i . Også for lineære funksjoner dropper en ofte parentesene, der dette er mulig uten å miste lesbarhet.
Bruken av omvendt polsk notasjon kan også i noen tilfeller eliminere behovet for parenteser. I denne notasjonen skrives funksjonen som . For eksempel er fakultetsfunksjonen som regel skrevet , selv om den relaterte gammafunksjonen skrives .
For å vise mengder relatert til en total funksjon, skriver en
- .
Verdimengden skrives gjerne som .
En komplett beskrivelse av en funksjon involverer navnet, definisjonsmengden, verdiområdet og en definisjon av den binære relasjonen. Derfor ser en ofte ulike former for todelt notasjon, som i
og også
I dette eksempelet er funksjonen kalt «», og denne har de naturlige tallene som definisjonsmengde og de reelle tallene som verdiområde. Funksjonen avbilder på seg selv, delt på¨.
For sammensatte funksjoner kan det være hensiktsmessig å plassere funksjonsnavnet over pilen mellom mengdene som er involvert:
Her er en funksjon fra mengden til mengden , mens er en funksjon fra til .
Spesifikasjon av funksjoner[rediger | rediger kilde]
En gitt funksjon kan spesifiseres på flere måter, og avsnittet beskriver vanlige måter.
Ved listing av ordnede par[rediger | rediger kilde]
En funksjon kan spesifiseres fullt og helt ved å liste opp alle ordnede par som inngår i definisjonen. Dersom definisjonsmengden er , så kan en definere en funksjon ved
[rediger | rediger kilde]
Matematikk inneholder en lang rekke funksjoner som er så viktige at de er gitt egne navn og symboler. Dette omfatter elementære grunnfunksjoner (se eget avsnitt) og også mer spesielle funksjoner, som for eksempel gammafunksjonen, Heaviside-funksjonen, Eulers totientfunksjon og feilfunksjonen.
Ved formel[rediger | rediger kilde]
En funksjon blir ofte spesifisert ved hjelp av matematiske symboler, som en formel. Et eksempel på en slik formelspesifikasjon kan være .
Som inverse funksjon[rediger | rediger kilde]
En funksjon sies å være bijektiv dersom funksjonen definerer en-til-en korrespondanse mellom elementer i og elementer i . Det vil si at det for hvert element i eksisterer ett og kun ett element slik at . For slike funksjoner er det mulig å definere den inverse funksjonen som avbilder på .[21]
Den reelle logaritmefunksjonen er eksempel på en bijektiv funksjon fra mengden av positive reelle tall inn på mengden av reelle tall. Funksjonen har en invers funksjon, som er eksponentialfunksjonen.
Selv om en funksjon ikke er bijektiv, så kan en i noen tilfeller velge undermengder og , slik at restriksjonen av funksjonen er bijektiv fra til . Den inverse funksjonen vil da eksistere begrenset til disse mengdene. De inverse trigonometriske funksjonene er definert på denne måten. For eksempel er cosinus-funksjonen en bijeksjon fra intervallet , og den inverse funksjonen arcus-cosinus har definisjonsmengde .
Som implisitt funksjon[rediger | rediger kilde]
Mange binære relasjoner mellom to mengder og vil være av en slik form at de for hvert element i entydig definerer et element . Slike relasjoner vil definere en implisitt funksjon[22] Den binære relasjonen som definerer den implisitte funksjonen, er som oftest en ligning. Inverse funksjoner er en type funksjoner som er definert implisitt, ved en enkel ligning .
Som et eksempel vil ligningen for enhetssirkelen
være en relasjon mellom og . For for de fleste verdiene av i intervallet [-1,1] definerer denne to verdier av , en positiv og en negativ. Det vil si at relasjonen definerer to funksjoner implisitt, en med verdimengde [-1,0] og en med verdimengden [0,1]. I dette enkle tilfellet er det mulig å uttrykke de to funksjonene eksplisitt:
I mer kompliserte tilfeller er det ikke mulig å definere en implisitt funksjon på en eksplisitt form.
Tilstrekkelige vilkår for at en funksjonsrelasjon definerer implisitt som funksjon av er gitt ved det implisitte funksjonsteorem.[23]
Som sammensatt funksjon[rediger | rediger kilde]
En funksjon kan spesifiseres som en sammensatt funksjon, også kalt et produkt, av to eller flere andre funksjoner. La og . En sammensatt funksjon er definert ved[24]
Verdimengden til er en delmengde av . En sammensatt funksjon kan skrives som . Et eksempel på en sammensatt funksjon er gitt ved
Ved differensialregning[rediger | rediger kilde]
Mange funksjoner er definert som løsningen av en differensialligning. I det enkleste tilfellet inkluderer dette alle funksjoner som er en antiderivert av en annen funksjon, det vil si som er løsning av en ligning av typen
Mer komplekse eksempler inkluderer Bessel-funksjoner, Legendre-funksjoner og den hypergeometriske funksjonen.
Ved rekursjon[rediger | rediger kilde]
Funksjoner med definisjonsmengde lik mengden av naturlige tall kan defineres ved hjelp av rekursjon, det vil si at funksjonsverdien for blir definert som en funksjon av funksjonsverdier svarende til argument mindre enn :
Her er funksjonen definert ved et endelig antall aritmetiske operasjoner på argumentene. En følge er en type funksjon som ofte blir definert på denne måten.
Representasjon av funksjoner[rediger | rediger kilde]
I tillegg til en formell spesifikasjon, kan en funksjon representeres på flere måter som gir en forenklet fremstilling av variasjon i funksjonen. Dette gjelder spesielt for reelle funksjoner, det vil si funksjoner der verdiområdet er mengden av reelle tall.
Graf[rediger | rediger kilde]
Grafen til en funksjon er formelt definert som
For en reell funksjon av en reell variabel vil mengden av ordnede par svare til en mengde av punkt i et todimensjonalt koordinatsystem, og en visuell fremstilling av denne punktmengden omtales vanligvis som en kurve, som et plott eller som en graf til funksjonen.
Tabell[rediger | rediger kilde]
En tabell kan gi en komplett eller en ikke-komplett framstilling av en funksjon. Eksempler er
- Tabeller som viser portotakster som funksjon av brevvekt og lengde på forsendelsen
- Logaritmetabeller som viser logaritmefunksjonen for utvalgte verdier
Dersom tabellen ikke er fullstendig, så kan interpolasjon brukes for å finne mellomliggende verdier.
Diagrammer[rediger | rediger kilde]
For funksjoner som har en endelig mengde som definisjonsområde, kan et søylediagram (stolpediagram) brukes til å representere funksjonen. I et slikt diagram er høyden på søylen proporsjonal med funksjonsverdien.
Funksjoner med et endelig definisjonsområde kan også representeres i sektordiagram (sirkeldiagram, kakediagram). Buelengden til hver sektor er proporsjonal med funksjonsverdien. Det finnes en rekke spesialiserte varianter av sektordiagrammer, som for eksempel rosediagrammer.
Egenskaper til funksjoner[rediger | rediger kilde]
Funksjoner kan karakteriseres med en lang rekke egenskaper, og egenskapene kan brukes til å kategorisere funksjoner i klasser og funksjonsrom. Her er bare omtalt noen få viktige egenskaper.
Injektivitet, surjektivitet og bijektivitet[rediger | rediger kilde]
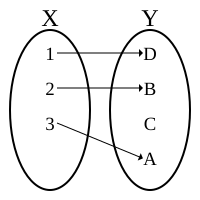
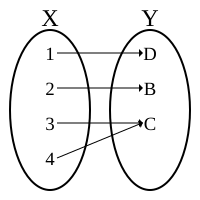
En funksjon er injektiv hvis den for ethvert element i verdimengden til funksjonen svarer bare til maksimum én verdi i definisjonsmengden. En slik funksjon kalles en injeksjon og også en en-til-en-funksjon. En funksjon er surjektiv hvis den for ethvert element i verdimengden svarer til minst én verdi i definisjonsmengden. En funksjon er bijektiv hvis den for ethvert element i verdimengden svarer til nøyaktig én verdi i definisjonsmengden.
 |
 |
 |
Symmetrier[rediger | rediger kilde]
En funksjon er jevn eller jamn dersom den har symmetriegenskapen . For en reell funksjon av en reell variabel svarer dette til at grafen til funksjonen er symmetrisk om -aksen. En odde funksjon oppfyller egenskapen . Grafen til en odde reell funksjon av en variabel er symmetrisk om origo.
En funksjon av flere variable er symmetrisk dersom den er uendret ved permutasjoner av argumentene, for eksempel
Kontinuitet[rediger | rediger kilde]
En funksjon er kontinuerlig for et argument dersom den oppfyller et vilkår
Definisjonen krever at størrelsene på begge sider av likhetstegnet er definert. Det eksisterer flere alternative definisjoner av det viktige begrepet kontinuitet. Funksjonen sies å være kontinuerlig i et område dersom den er kontinuerlig for alle elementer i området. En kontinuerlig funksjon kan uformelt karakteriseres som «sammenhengende». Et punkt der funksjonen ikke er kontinuerlig, kalles en diskontinuitet
Deriverbarhet[rediger | rediger kilde]
En funksjon er deriverbar i et punkt dersom den deriverte er definert i punktet. Funksjonen er deriverbar i et område dersom den er deriverbar for alle argument i området. En funksjon som har kontinuerlig førstederiverte, sies å være kontinuerlig deriverbar. For en glatt funksjon er alle deriverte av alle ordener kontinuerlige.
En kompleks funksjon er deriverbar dersom den oppfyller Cauchy-Riemann-ligningene. En holomorf funksjon er en kompleks funksjon som er deriverbar i hele definisjonsmengden.
Funksjonstyper[rediger | rediger kilde]
Funksjoner kan deles inn i en lang rekke forskjellige typer, klasser og funksjonsrom, og her nevnes kun et par viktige typer.
For en oversikt over funksjoner omtalt på Wikipedia, se Kategori:Funksjoner.
Elementære grunnfunksjoner[rediger | rediger kilde]
Til de elementære grunnfunksjonene av en reell eller kompleks variable regnes[25]
- De rasjonale funksjonene, inkludert polynomfunksjonene
- Eksponentialfunksjonen
- Logaritmefunksjonen
- Trigonometriske funksjoner, inkludert arcus-funksjonene
- Den generelle potensfunksjonen
Elementære funksjoner[rediger | rediger kilde]
En elementær funksjon er en funksjon sammensatt av elementære grunnfunksjoner, ved hjelp av et endelig antall aritmetiske operasjoner; addisjon, subtraksjon, multiplikasjon og divisjon. I tillegg regner også sammensatte funksjoner av elementære funksjoner som elementære.[25]
Linære funksjoner[rediger | rediger kilde]
Begrepet lineær funksjon kan brukes på to ulike måter: I reell analyse kaller en ofte funksjonen for en lineær funksjon. Grafen til denne funksjonen er en rett linje. I lineær algebra er en lineær funksjon en funksjon som oppfyller ligningen
I lineær algebra er altså funksjonen kun lineær dersom konstanten er lik null.
Aritmetiske funksjoner[rediger | rediger kilde]
I tallteori benyttes aritmetiske funksjoner. De har som argument et naturlig tall n og gir et lignende tall ut. Et eksempel ville være en potens ns der s er et heltall. En av de mest kjente, aritmetiske funksjoner er Eulers totientfunksjon.[26]
Algerbraiske og transcendente funksjoner[rediger | rediger kilde]
En algebraisk funksjon er en funksjon som kan være en løsning av en algebraisk ligning i en eller flere reelle eller komplekse variable. Alle rasjonale funksjoner er algebraiske.
En funksjon som ikke er algebraisk, er en transcendent funksjon. Logaritmefunksjonen, eksponentialfunksjonen og gammafunksjonen er alle transcendente funksjoner.
Analytiske funksjoner[rediger | rediger kilde]
En reell eller en kompleks funksjon er analytisk i en omegn til et punkt dersom den kan utvikles i en konvergent potensrekke omkring punktet. En funksjon som er analytisk i hele det komplekse planet, kalles en hel funksjon. Analytiske funksjoner kan altså utvikles i konvergente potensrekker. Eksempler på analytiske funksjoner er
Derivasjon[rediger | rediger kilde]

Utdypende artikkel: Derivasjon
En derivert av en funksjon er et mål for den momentane endringen til funksjonen. For en reell eller kompleks funksjon av én variabel er den deriverte i et punkt definert ved
- ,
forutsatt at grensen eksisterer. Funksjonen sies da å være differensierbar eller deriverbar i . En kompleks funksjon som er differensierbar i hele definisjonsområdet, kalles en holomorf funksjon.
En funksjon som er deriverbar i et punkt, vil også være kontinuerlig i punktet.
For reelle funksjoner av flere variable uttrykker en partiell derivert variasjonen til funksjonen når én av variablene endres og de andre holdes konstant. Den retningsderiverte av en slik funksjon er et mål for endringen i en gitt retning. Gradienten er en vektor som peker i den retningen funksjonen endrer seg mest.
En Gateaux-derivert for en funksjon er en generalisering av den retningsderiverte. En Frechet-derivert generaliserer teori for den deriverte til en reell funksjon av en variabel til et Banach-rom.
Integrasjon[rediger | rediger kilde]

Utdypende artikkel: Integrasjon
Integralet av en reell funksjon av en variabel kan defineres uformelt som arealet under grafen til funksjonen. Formelt defineres integralet over et intervall vanligvis som en grenseverdi for en sum av rektangulære areal, når bredden av hvert rektangel går mot null og antall rektangler mot uendelig. Et slik integral kalles et Darboux-integral eller et Riemann-integral. En funksjon der grenseverdien eksisterer kalles integrerbar. Integrasjon over et intervall kalles også å finne det bestemte integralet.
Det ubestemte integralet eller den antideriverte av en funksjon er en ny funksjon som har funksjonen som derivert, det vil si . Funksjonen kalles også en primitiv funksjon til . Det ubestemte integralet er relatert til det bestemte integralet gjennom analysens fundamentalteorem. Derivasjon og integrasjon er dermed inverse operasjoner.
En funksjon kan også integreres langs en kurve, i et linjeintegral. En funksjon av flere variable kan integreres over en flate, i et flateintegral. Et volumintegral er et integral over et tredimensjonalt område, et volum.
Det eksisterer flere generaliserte integral, definert for å kunne omfatte en større gruppe av funksjoner som integrerbare. Slike generaliseringer er Riemann–Stieltje-integral og Lebesgue-integral.
Se også[rediger | rediger kilde]
- Funksjonsdrøfting
- Funksjonslære i norsk skole
- Isomorfisme
- Ligning (matematikk)
- Matematisk analyse
- Proporsjonalitet
Referanser[rediger | rediger kilde]
- ^ : C.B.Boyer; A history of mathematics s.26ff
- ^ : C.B.Boyer; A history of mathematics s.179f
- ^ M. Abramowitz, I.A. Stegun, red. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (PDF). Applied Mathematics Series 55. New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. [Tiende opptrykk, 1974]
- ^ : C.B.Boyer; A history of mathematics s.289ff
- ^ João Pedro da Ponte (1992). «The history of the concept of function and some educational implications». The Mathematics Educator (engelsk). 3 (2). Arkivert fra originalen 23. desember 2019. Besøkt 23. desember 2019.
- ^ a b c Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. s. 97. ISBN 0-88385-511-9.
- ^ a b c F. Cajori (2007). A History of Mathematical Notations. II. New York: Cosimo. s. 62.
- ^ : C.B.Boyer; A history of mathematics s.533
- ^ : C.B.Boyer; A history of mathematics s.554ff
- ^ : C.B.Boyer; A history of mathematics s.565
- ^ : C.B.Boyer; A history of mathematics s.598ff
- ^ Godfrey Harold Hardy (1908). A Course in Pure Mathematics. Cambridge, UK: Cambridge University. ISBN 0-521-09227-2. s.26-28. Originalsitat: «to some values of at any rate correspond values of ».
- ^ Jean Luc Dorier (1995). «A general outline of the genesis of vector space theory». Historia mathematica (engelsk). 22 (3): 227-261.
- ^ M. Bernkopf (1966). «The development of function spaces with particular reference to their origins in integral equation theory». Archive for History of Exact Sciences (engelsk). 3: 1-96.
- ^ Jens Lindström (Januar 2008). On the origin and early history of functional analysis (PDF). U.U.D.M. Project Report 2008:1 (avhandling) (engelsk). Department of Mathematics, Uppsala University. s. 1-62.
- ^ a b Hans Fredrik Aas (1974). Forelesningsnotater i matematisk analyse. I. Bergen: Matematisk institutt, Universitetet i Bergen. s. 6.
- ^ a b : R.D. Milne; Applied functional analysis... s.11
- ^ R. Bartle (2001). The Elements of Real Analysis. John Wiley and Sons. ISBN 0-471-05464-X.
- ^ : G. Thomas, R. Finney; Calculus and Analytic Geometry s.17
- ^ R.V Churchill, J.W. Brown, R.F. Verhey (1974). Complex variables and applications. Tokyo: McGraw-Hill Kogakusha. ISBN 0-07-010855-2.
- ^ Hans Fredrik Aas (1974). Forelesningsnotater i matematisk analyse. I. Bergen: Matematisk institutt, Universitetet i Bergen. s. 57.
- ^ : G. Thomas, R. Finney; Calculus and Analytic Geometry s.79
- ^ T.M. Apostol (1969). Calculus. II. New York: John Wiley & Sons. s. 62. ISBN 0-471-00008-6. s.62
- ^ : R.D. Milne; Applied functional analysis... s.12
- ^ a b Hans Fredrik Aas (1974). Forelesningsnotater i matematisk analyse. I. Bergen: Matematisk institutt, Universitetet i Bergen. s. 62.
- ^ T.M. Apostol, Introduction to Analytical Number Theory, Springer-Verlag, New York (1976). ISBN 0-387-90163-9.
Litteratur[rediger | rediger kilde]
- G. Thomas, R. Finney (1995). Calculus and analytic geometry (9th edition utg.). Reading, USA: Addison-Wesley. ISBN 0-201-53174-7.
- Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
- N.N. Lebedev (Oversatt og redigert av R.A Silverman) (1972). Special functions and applications. I. New York: Dover Publications. ISBN 0-486-60624-4.
- C.B.Boyer (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
























































![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle {\begin{alignedat}{3}f(x)&=&{\sqrt {1-x^{2}}}\qquad x\in [-1,1]\\[4pt]g(x)&=-&{\sqrt {1-x^{2}}}\qquad x\in [-1,1]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30086352ec27d8a188db584634384c262e30d926)
























