Kjeglesnitt


Et kjeglesnitt er en kurve, laget som en skjæringslinje mellom et plan og en kjegleflate.[1] Avhengig av retningen til planet i forhold til kjeglen vil kjeglesnittet være en ellipse, parabel eller hyperbel. En sirkel er et spesialtilfelle av en ellipse. For noen plasseringer av planet kan kjeglesnittet degenere til et punkt, en linje eller to linjer.
Kjeglesnitt kan defineres på mange forskjellige måter. Geometrisk kan kjeglesnitt defineres som det geometrisk sted for punkter i planet hvis avstand til et gitt punkt er proporsjonal med avstanden og til en gitt linje. Punktet kalles fokus eller brennpunkt, og linjen kalles direktrise eller styrelinje. Proporsjonalitetskonstanten kalles eksentrisiteten e, og denne karakteriserer formen til kjeglesnittet. En hyperbel er en åpen kurve med e > 1 og to adskilte grener. En parabel har eksentrisitet e = 1 og er også en åpen kurve. Ellipsen er en lukket kurve med e < 1. En sirkel kan betraktes som et spesialtilfelle med eksentrisitet e = 0. I analytisk geometri er et kjeglesnitt definert som en kurve av andre orden i to variable, og omvendt vil en algebraisk kvadratisk ligning i to variable alltid framstille et kjeglesnitt.
Egenskapene til kjeglesnitt ble utforsket av greske matematikere for over to tusen år siden, etter først å ha blitt beskrevet av Menaikhmos på 300-tallet f.Kr. Spesielt viktig var bidraget til Apollonios fra Perge, og læreverket Kjeglesnitt ble et av de mest studerte i fra antikkens Hellas. Apollonios innførte navnene ellipse, parabel og hyperbel. Studiet av kjeglesnitt fortsatte med stor intensitet også i nyere europeisk matematikk.
Historie[rediger | rediger kilde]
Sirkelen er en av de eldste studerte geometriske formene. Også ellipsen har sannsynligvis vært kjent i svært lang tid, da formen oppstår i mange daglige situasjoner. For eksempel opptrer en ellipse når en sirkel sees fra siden og når en sylindrisk trestamme blir kuttet skjevt i to stykker. Lys som går gjennom et lite sirkulært hull og treffer skjevt på en vegg vil også synes som en ellipse: Lyset danner en kjegle som blir kuttet over av veggen.
Menaikhmos og tidlige arbeid[rediger | rediger kilde]
Kjeglesnitt ble sannsynligvis introdusert av den greske matematikeren Menaikhmos på 300-tallet f.Kr.[2] Ingen arbeid etter Menaikhmos er bevart, men noen av resultatene hans er omtalt av andre greske matematikere. Fra disse vet vi at Menaikhmos oppdaget kjeglesnittene i arbeid med å løse det deliske problem, knyttet til fordobling av volumet av en kube.[3] Hippokrates hadde vist at dette problemet er ekvivalent med å finne to størrelser og , slik at
når og er to kjente størrelser. Fra dette følger det at , slik at volumet av kuben med sidelengde kan dobles ved å velge og så bestemme . Det var på denne formen Menaikhmos prøvde å løse problemet. Grekerne hadde imidlertid ikke algebra, men uttrykte forholdene geometrisk. Med dagens algebra ser en umiddelbart at problemet kan løses ved å finne verdien av som gir skjæring mellom to parabler og , alternativt mellom en av parablene og hyperbelen .
Etter omtalen fant Menaikhmos disse kurvene som snitt mellom en kjegle og et plan. Selv om parabelen og hyperbelen var av primær interesse, har han også oppdaget at ellipsen kunne genereres på denne måten. Det er ikke kjent hva som motiverte Menaikhmos til å studere kjeglen. I tidlig gresk matematikk var en kjegle alltid rett, med en sirkulær grunnflate, dannet ved å rotere en rettvinklet trekant omkring den ene kateten. Basert på toppvinkelen kunne kjegler karakteriseres som spiss, rett eller stump. De tidlige arbeidene brukte ikke navn som hyperbel, parabel og ellipse, men beskrev kurvene som «snitt gjennom en spiss/rett/stump kjegle». Navnene viser at en har definert kjeglesnittene ved å snitte kjeglen med et plan som står normalt på hypotenusen i den roterte trekanten, det vil si normalt på en generatrise i kjegleflaten.
Ifølge Pappos skal Aristaios den eldre omkring 350 f.Kr. ha laget «fem bøker om romlige geometriske steder, knyttet til kjeglesnitt». Pappos omtaler også «kjeglesnittene til Aristaios den eldre».[4] Et geometrisk sted ble i gresk matematikk omtalt som «romlig» dersom en trengte et romlig objekt for å definere dette, og i praksis var i senere gresk matematikk et romlig geometrisk sted det samme som et kjeglesnitt. I motsetning til dette ble linjer og sirkler kalt «plane geometriske steder». Thomas Heath argumenterer for at Aristaios må ha kjent til definisjonen av et kjeglesnitt basert på et brennpunkt og en styrelinje.[5]
Også Evklid (født ca 300 f.Kr.) skal ha skrevet fire bøker om kjeglesnitt, men ingenting av dette er bevart. Det er sannsynlig at Aristaios verk om kjeglesnittene var eldre enn Evklids boks om samme emne og at Evklid har basert sin bok på resultater fra Aristaios.[4] Evklid sitt berømte verk Elementer inneholder materiale om sirkelen, men ikke om kjeglesnitt. I verket Phenomena viser Evklid at han er kjent med at en ellipse kan dannes når et plan skjærer en kjegle eller en sylinder skrått.
Flere at verkene til Arkimedes (født ca 287 f.Kr.) behandler kjeglesnitt, og han viser at han må ha kjent til resultatene til Menaikhmos og Euklid. Ved å bruke ekshausjonsbevis kunne Arkimedes beregne arealet under et segment av en parabel, og også volumet under det tilsvarende rotasjonslegemet. Arkimedes fant også uttrykk for arealet av en ellipse. Tittelen på verket Kvadrering av parabelen kan være gitt i ettertid, og det er usikkert om Arkimedes selv brukte navnet «parabel».
Apollonios fra Perge[rediger | rediger kilde]

Navnene hyperbel, parabel og ellipse er først kjent fra det viktige verket Kjeglesnitt, skrevet av Apollonios på 200-tallet f.Kr. I dette samler han og videreutvikler tidligere kunnskap om kjeglesnittene. Sammen med Elementer av Evklid er dette kanskje det viktigste vitenskapelig arbeidet fra antikken, ofte studert og beundret av senere matematikere. Apollonios viste at alle kjeglesnittene kan dannes ved å snitte en og samme kjegle med et plan i forskjellige vinkler relativt til kjegleaksen. Kjeglen kan også være skrå. I tillegg utvidet Apollonios definisjonen av en kjegle til å omfatte to kapper, det vil si to deler med et felles toppunkt. På den måten kan en få dannet to sammenhørende hyperbel- og parabelgrener fra ett og samme snitt.
I studiet av kvadratiske ligninger hadde pytagoreerne innført begrepene hyperbel, parabel og ellipse for å karakterisere arealet av et rektangel sammenlignet med et kvadrat. Et tilfelle der arealene var like ble kalt «parabel» (para = nær opp til, ballein = å kaste), et tilfelle der rektangelet var mindre enn kvadratet ble omtalt som «ellipse» (en =i, leipein=å utelate), mens det siste alternativet ble kalt «hyperbel» (hyper=over, ballein = å kaste). Ligningen for en parabel kan tolkes som at arealet av et rektangel med sidekant har samme areal som et rektangel med sidekanter og . I en ellipse er produktet mindre enn kvadratet og i en hyperbel større. I geometriske betraktninger var størrelsen så viktig at den ble gitt et eget navn, på latin latus rectum («rett korde»).
Kjeglesnitt inneholder syv kjente og bevarte bøker, de fire første fra gresk og de tre siste fra arabisk.[5] En vet også at et åttende bind har eksistert, men dette har gått tapt. De tre første bindene er antatt å være oppsummering og presentasjon av resultatene fra Menaikhmos og Evklid, men også med egne bidrag fra Apollonios.
Litt overraskende omtaler Apollonius ikke kjeglesnitt som det geometriske sted for et punkt som har en avstand til et gitt punkt proporsjonal med avstanden og til en gitt linje. Denne egenskapene ble først beskrevet av den greske matematikeren Pappos som arbeidet hundre år senere i Alexandria.[6] Pappos brukte kjeglesnitt til å løse problemet med vinkelens tredeling, et klassisk problem i gresk matematikk.
Arven etter Apollonius[rediger | rediger kilde]
Kjeglesnitt av Apollonios ble stående som det autoritative verket om emnet. I ettertiden ble det ble skrevet flere kommentarer til verket og det ble hyppig referert, uten at det ble tilført vesentlig nytt. Et viktig verk ble likevel Om brennende speil, skrevet av Anthemios fra Tralles (født ca 474). Tralles var det greske navnet på den tyrkiske byen Aydın. I dette arbeidet beskriver Anthemios hvordan kjeglesnitt kan brukes til å samle solstråler i et fast punkt, også når solen flytter seg på himmelen.[7]

Da interessen for matematikk gradvis forsvant i det antikke Hellas, ble mye av kunnskapen tatt vare på og videreutviklet i Midtøsten. Apollonius Kjeglesnitt ble oversatt til arabisk av Thābit ibn Qurra, født 826.[8] Den arabiske astronomen Ibn al-Haitham (født 965) var en pioner i optikk og fortsatte arbeidet med koniske speil. Han baserte seg tungt på Apollonius og etterlot seg en hånskrevet kopi av Kjeglesnitt.[9]
Et instrument for å tegne kjeglesnitt ble beskrevet i 1000 e.Kr. av den muslimske matematikeren Al-Kuhi. Muslimske matematikere var opptatt av algebraiske ligninger, og perseren Omar Khayyám (født 1048) oppdaget at løsningen av visse kubiske ligninger kunne finnes som skjæringspunkt mellom to kjeglesnitt:[8] Gitt ligningen
Ved å substituere , så kan denne ligningen skrives som
Den første ligningen er en parabel og den siste en hyperbel, og løsningen av tredjegradsligningen er gitt ved skjæringen mellom disse. Khayyám kunne ikke håndtere negative koeffisienter, og problemet ble delt opp i en rekke delproblem, avhengig av verdiene til koeffisientene a, b og c.
Kjeglesnitt i tidlig europeisk matematikk[rediger | rediger kilde]
Apollonios Kjeglesnitt var lenge lite kjent i Europa, men en oversetting til latin av de fire første bøkene ble gitt ut i Venezia i 1537. Det tok også lang tid før arbeidet til Pappos ble gjenoppdaget. Johannes Werner (1468-1522) kjente antageleig ikke til Apollonius' arbeid da han i 1522 i Nürnberg fikk trykket 22 bøker med tittel Elementer av kjeglesnitt. Bøkene inneholder lite nytt ut over det Apollonius hadde vært i stand til å finne.[10] Imidlertid vekket bøkene opp igjen interessen for kjeglesnitt og stimulere interessen for å rekonstruere arbeidet til de tidlige greske matematikerne.
Våpenkappløpet hadde ført til utvikling av kanoner som kynne skyte lenger enn synsfeltet, og dette gjorde det viktig å kunne forutsi hvor en kanonkulen ville lande. De første tilløpene til beskrivelse brukte trekanter og sirkler for å beskrive kulebanen. Galileo Galilei (1564-1642) var den første til å vise at kulebanen kan beskrives med en parabel.[11]
Arkimedes hadde vært i stand til å finne volumet i en omdreiningsparaboloide, men hadde ikke vært i stand til å behandle hyperbelen tilsvarende, da dette krever transcendente funksjoner. Dersom en roterer den positive grenen av hyperbelen , så dannes i intervallet et romlig legeme kalt «Torricellis vinglass», «Torricellis trompet» og også «Gabriels horn». Den italienske matematikeren Evangelista Torricelli (1608-1647) var den første som påpekte «malerparadokset»: volumet av dette rotasjonslegement er endelig, mens arealet er uendelig.[12]
Kjeglesnitt i optikk og astronomi[rediger | rediger kilde]

Optikk var vikitg både for skipsfart og for astronomi. Interessen til Johannes Kepler (1571-1630) for kjeglesnitt var først motivert av studier i optikk og egenskaper til parabolske speil.[13] I 1604 ga han ut Ad Vitellionem paralipomenaa («Om Vitellos optikk»), der han definerer kjeglesnitene ut fra to punkt, som Kepler kaller «foci» eller «brennpunkt». Det latinske ordet «focus» betyr «ovn, ildsted», og ordet kunne betegne både et varmesenter og et samlingspunkt.[14] Kepler så på kjeglesnitt som kurver i én og samme familie: Fra degenererte kjeglesnitt i form av rette linjer gjennom et felles brennpunkt, får en dannet hyperbler når brennpunktene fjerner seg fra hverandre. Når ett av brennpunktene er i uendelig har man en parabel. Dersom dette brennpunktet passerer gjennom uendelig og dukker opp på motsatt side, så dannes ellipser. Til slutt ender en opp med en sirkel, når brennpunktene igjen faller sammen. Med denne behandlingen av et punkt i uendelig legger Kepler også grunnen for projektiv geometri.
Kjeglesnittene skulle også spille en viktig rolle i Keplers lover for planetenes bevegelser. Planetene beveger seg i elliptiske baner med solen i det ene brennpunktet. I ettertiden er det vist at ikke-periodiske kometer vil kunne følge ubundne parabel- eller hyperbelbaner.[15]
Det første teleskopet som utnyttet speil ble konstruert av James Gregory (1638-1675). Det hadde et primært speil som var parabolsk og et sekundært som var ellipseformet. Speilteleskop basert på former av kjeglesnitt ble konstruert også av Isaac Newton (1642-1726) og av Guillaume Cassegrain (1629-1693).[16]
Projektiv og analytisk geometri[rediger | rediger kilde]

På 1600-tallet var det stor interesse for bruk av sentralperspektiv i malerkunsten. Sammen med Kjeglesnitt av Apollonius inspirerte dette franskmannen Girard Desargues (1591-1661) til i 1639 å gi ut boken med den omstendelige tittelen Brouillon projet d'une atteinte aux évenement des recontres d'une cone avec un plan («Et grovt utkast på et forsøk på å behandle et møte mellom en kjegle og et plan»)[17]. Her legger Desargues grunnen for projektiv geometri, ved å behandle egenskaper ved kjeglesnitt som er uendret når kjeglesnittet blir projisert mot et punkt. Når en sirkel projiseres dannes det nettopp en kjegle.
Blaise Pascal (1623-1662) var elev av Desargues og var bare 16 år gammel da han ga ut Essay pour les coniques («Essay om kjeglesnittene»). Denne artikkelen var bare på én enkelt side og inneholdt det forfatteren selv kalte hexagrammum mysticum, senere kalt Pascals teorem. Det omtaler egenskaper til et heksagon innskrevet i en ellipse. Pascal skal også ha gitt ut et senere verk om kjeglesnitt, men dette har gått tapt.[17] Også en annen elev av Desargues, Philippe de La Hire (1640-1718), ga i 1685 ut et verk om kjeglesnitt. La Hires teorem omhandler tangenter til kjeglesnitt.[18] Charles Brianchon (1783-1864) ga Pascals teorem en modernisert form og beviste det som nå kalles Brianchons teorem for et heksagon omskrevet om en ellipse. Pascals teroem og Brianchons teorem er begge grunnleggende for studiet av kjeglesnitt i projektiv geometri og sammen et eksempel på «duale» teorem i geometri - teorem som er gyldige dersom ordene «linje» og «punkt» bytter plass.[19]
Arbeid med projektiv geometri ble videreført og systematisert av Jean-Victor Poncelet (1788-1867). Poncelets tillukningsteorem omhandler et polygon som er innskrevet i ett kjeglesnitt og omskrevet i et annet.
Ved å legge grunnen for analytisk geometri gjorde René Descartes (1596-1650) og Pierre de Fermat (1601-1665) det mulig å behandle kjeglesnittene algebraisk. For begge disse matematikerne var Kjeglesnitt av Apollonios en viktig inspirasjon. I bok III presenterer Apollonios kjeglesnitt som det geometriske sted for et punkt der avstanden til tre eller fire linjer har et bestemt forhold. Med tre linjer skal produktet av avstandene til to av linjene være lik kvadratet av avstanden til den tredje linjen. Med fire linjer skal produktet av avstandene til to av linjene være lik produktet av avstandene til de to andre linjene. Det var en generalisert form for dette resultatet Descartes brukte til å utforske bruken av koordinater, etter forslag fra Jacob Golius (1596-1667). Fermat viste at andregradsuttrykk kunne brukes til å definere hyperbler, parabler og ellipser, og også at transformasjoner kunne brukes til å omforme generelle andregradsuttrykk til standardformer for kjeglesnittene.
Descartes La géométrie var ikke lett tilgjengelig i formen, og det ble gitt ut flere kommentarer til verket. Johan de Witt (1629-1672) brukte Descartes koordinatdefinisjoner til å studere kjeglesnitt i kommentarverket Elementa curvarum, som ble utgitt omkring 1660. Her reduserer han alle andregradsligninger i to variable til kanoniske former, ved en translasjon og rotasjon av aksene.[20] Han bruker også diskriminanten for å skille tilfeller der ligningen gir hyperbler, parabler og ellipser. Betegnelsen «direktrise» kommer fra de Witt. Det latinske «directrix» betyr «hun som styrer», der hunkjønnsformen ble brukt fordi ordet «linje» på latin (linea) er hunkjønn.[21] Samtidig med de Witt publiserte John Wallis (1616-1703) i England et verk med omtrent tilsvarende innhold.[20]
Giulio di Fagnano (1682-1766) forsøkte å beregne buelengde av en ellipse, men støtte på problemer med å utføre det nødvendige integrasjonen. Integralet er et elliptisk integral, som dermed har et opphav knyttet til kjeglesnitt.
Nyere tid[rediger | rediger kilde]
Lazare Carnot (1753-1823) viste at kjeglesnittene kunne relaterte seg til hverandre, dersom en tillot komplekse koeffisienter i andregradsligningene. Carnots teorem beskriver en sammenheng mellom skjæringspunktene som kan opptre mellom en trekant og et kjeglesnitt.
De engelske matematikerne James Joseph Sylvester (1814-1897) og Arthur Cayley (1821-1895) brukte matriser og determinanter til å studere polynomuttrykk i både to og flere variable, og kartla også størrelser for kjeglesnitt som er invariante under transformasjoner. Sylvester er opphavsmannen til begrepet «diskriminant».
Arbeid med projektiv geometri ble videreført av Jakob Steiner (1796-1863), og han innførte en alternativ metode for å definere kjeglesnitt i projektiv geometri. I enumerativ geometri gjelder det å telle antall geometriske objekter av en viss type, og dette er også utfordringen i Steiners problem: Gitt fem vilkårlige kjeglesnitt i det komplekse planet. Finn et nytt kjeglesnitt som tangerer de andre fem. Steiner selv ga eit feilaktig svar på problemet, som først fant sin rette løsning (3264) etter Steiners død.[22]
Nullpunkt i multivariate polynomer blir i dag studert i algebraisk geometri.
Geometriske definisjoner[rediger | rediger kilde]
Ved snitt gjennom en kjegle[rediger | rediger kilde]

Gitt en rett kjegleflate A med sirkulær basis, der toppvinkelen er lik . La B være et plan som skjærer kjegleflaten, med en vinkel relativt til aksen i kjegleflaten. Skjæringslinjen mellom de to flatene A og B er et kjeglesnitt, og formen på kjeglesnittet avhenger av forholdet mellom de to vinklene:
Eksentrisiteten til kjeglesnittet er gitt ved[1]
Kjeglesnittene vil være degenererte dersom planet går gjennom toppunktet til kjegleflaten.
Skjæringslinjen vil også være et kjeglesnitt dersom kjegleflaten er skrå eller har en ellipseformet basis.
Ved brennpunkt og styrelinje[rediger | rediger kilde]

Gitt en rett linje og et punkt som ikke ligger på linjen. Et kjeglesnitt er det geometriske sted for et punkt der avstanden til det valgte punktet er proporsjonal med avstanden til linjen. Linjen er kalt direktrisen eller styrelinjen, og punktet er kalt fokus eller brennpunktet.
Proporsjonalitetsfaktoren er kalt eksentrisiteten til kjeglesnittet. Et punkt på en parabel ligger like langt fra styrelinjen som fra brennpunktet, og . Et punkt på en ellipse ligger nærmere brennpunktet enn styrelinjen, og . For en hyperbel er , slik at et punkt på kurva ligger lenger fra brennpunktet enn fra styrelinjen.
En linje gjennom brennpunktet og normalt på styrelinjen er en akse i kjeglesnittet, og dette vil være symmetrisk om denne aksen.
En ellipse er symmetrisk om et senterpunkt, og det følger dermed at to sett av brennpunkter/styrelinjer vil gi samme ellipse. En ellipse har derfor to brennpunkter. En hyperbel består av to grener, hver med sin styrelinje og brennpunkt. En parabel kan også betraktes som å ha to brennpunkt, der det ene ligger i uendelig.
Definisjonen med bruk av styrelinje og brennpunkt vil ikke inkludere en sirkel som kjeglesnitt, men sirkelen kan betraktes som et grensetilfelle av en ellipse, når eksentrisiteten går mot null.
Når et plan A skjærer en rett kjegleflate K med sirkulær basis, så kan en plassere en kule inne i kjeglen, slik at denne tangerer både kjeglen og planet A. Legger en i tillegg et plan B gjennom den sirkelen der kulen tangerer kjegleflaten, så kan en vise at de to planene A og B skjærer hverandre langs direktrisen.[1] Tangeringspunktet mellom kuleflaten og planet A vil være brennpunktet, og dette gir en sammenheng mellom to geometriske definisjoner av kjeglesnitt.
Ved to brennpunkt[rediger | rediger kilde]
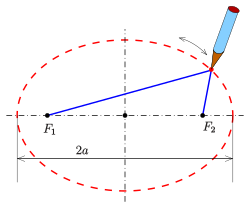
En ellipse kan defineres som det geometriske sted for et punkt der summen av avstandene til to gitte brennpunkter er konstant.[23] Dette har gitt opphavet til navnet gartnermetoden for å tegne en ellipse: Mellom to påler i jorda kan en knytte et tau som er lenger enn avtanden mellom pålene. Ved å føre en pinne innenfor tauet, som hele tiden holdes stramt, så vil pinnen tegne en ellipse.
En sirkel kan defineres som det geometriske sted for et punkt som ligger like langt fra et gitt senterpunkt.
En hyperbel kan defineres som det geometriske sted for et punkt der differensen av avstandene til to gitte brennpunkter er konstant.[23]
Andre geometriske steder[rediger | rediger kilde]
Det fines mange geometriske vilkår som leder fram til kjeglesnitt som geometrisk sted. Klassisk var Pappos problem for et gitt vilkårlig sett av rette linjer: Finn det geometriske sted slik at produktet av avstandene fra punktet til halvparten av linjene er lik produktet av avstandene til den andre halvparten. Med et odde antall rette linjer må avstanden til én av de rette linjene inngå med kvadratet i det tilhørende produktet. Det geometriske stedet vil være et kjeglesnitt.
Analytisk definisjon og standardformer[rediger | rediger kilde]
Kjeglesnitt kan defineres analytisk ved hjelp av flere ulike typer koordinater, og definisjonen kan gjøres helt frigjort fra geometriske definisjoner av kjeglesnitt. Formen på ligningen vil avhenge av typen koordinater og det valgte koordinatsystemet.
For hver type kjeglesnitt eksisterer det standardformer eller kanoniske former som presenterer kurvene på en enklest mulig form, definert ved et spesielt valg av koordinatsystem. Standardformene for nært knyttet til en geometrisk definisjon med bruk av brennpunkt og styrelinje: De fleste standardformene bruker en akse definert langs aksen i kjeglesnittet. For et kartesisk legges den andre aksen da parallelt med styrelinjen. Definisjon av origo kan imidlertid variere for ulike standardformer.
Et kvadratiske algebraisk uttrykk i to variabler og vil alltid framstille et kjeglesnitt, degenerert eller ekte, og ved en translasjon og en rotasjon vil ligningen alltid kunne overføres til en av standardformene.
Polarkoordinater[rediger | rediger kilde]
I figuren over til høyre er brennpunktet markert med bokstaven , og styrelinjen er definert i avstanden i fra brennpunktet. Det er naturlig å definere et polarkoordinatsystem med pol i brennpunktet og koordinatakse langs aksen til kjeglesnittet. Et punkt på kjeglesnittet er da definert ved polarkoordinatene . Etter den geometriske definisjonen med styrelinje og brennpunkt skal radiusen da være proporsjonal med avstanden fra styrelinjen til punktet :
Dette er ligningen for et kjeglesnitt i polarkoordinater. Lengden erstattes ofte med lengden av korden mellom to punkt på kjeglesnittet, gjennom brennpunktet vinkelrett på aksen. Denne størrelsen blir kalt latus rectum, og halve denne lengden blir kalt semi-latus rectum. Ved å sette følger det fra ligningen over at
Polarformen for kjeglesnittet kan dermed skrives på formen
Toppunktet (vertex) i kjeglesnittet er skjæringspunktet mellom kjeglesnittet og aksen. Avstanden mellom brennpunktet og toppunktet er gitt ved lengden :
Skilleligningen[rediger | rediger kilde]

Skilleligningen er en standardform for ligningen for kjeglesnitt i kartesiske koordinater. Ligningen fremkommer ved å legge -aksen langs aksen i kjeglesnittet, -aksen parallelt med styrelinjen og origo i toppunktet til kjeglesnittet:
Navnet reflekterer at ligningen skiller klart mellom de forskjellige typer kjeglesnitt, avhengig av størrelsen til eksentrisiteten .
Ligningen kan utledes fra polarkoordinat-formen for kjeglesnitt, på kvadrert form:
og ved å bruke sammenhengen mellom polarkoordinatene og de kartesiske koordinatene:
Kanonisk form for parabelen[rediger | rediger kilde]

En standardform for en parabel med toppunkt i origo og akse langs den positive -aksen er gitt fra skilleligningen når eksentrisiteten er lik 1:
Siden følger det at , og standardformen kan presenteres ved hjelp av både latus rectum , semi-latus rectum og abscissen til brennpunktet .[23]
For parabelen brukes i det videre , i analogi med de andre to kjeglesnitt-typene. Merk imidlertid at er en geometrisk lengde med lik definisjon for alle kjeglesnittene, mens definisjonen av varierer mellom kurvetypene.
Direktrisen er for parabelen definert ved .
En alternativ standardform bruker et aksesystem med brennpunktet som origo:[23]
Her er som før definert som avstanden mellom brennpunktet og toppunktet. Direktrisen er nå definert som .
Kanonisk form for ellipsen[rediger | rediger kilde]

Det eksisterer to alternative standardformer for en ellipse, definert enten med origo i det ene brennpunktet eller med origo i sentrum av ellipsen. Sentrum er definert som midtpunktet mellom de to brennpunktene.
Med origo i den ene brennpunktet er den kanoniske formen gitt som
I denne formen brukes lengden av halvaksene som parametre. Den store halvaksen er halve korden som går gjennom de to brennpunktene, og den lille havlvaksen står normalt på denne. Brennpunktene ligger i og . Direktrisen svarende til det første brennpunktet skjærer -aksen i , forutsatt at er større enn null.
Sammenhengen med skilleligningen og med de geometriske lengdene kan en finne ved å bruke skjæringspunktene mellom ellipsen og aksene, samt definisjonen av semi-latus rectum. Toppunktene der ellipsen skjærer -aksen er gitt ved , og ved å bruke lengden mellom brennpunktet og toppunktet får en
Fra definisjonen er semi-latus rectum den positive ordinaten for :
Ved isteden å bruke sentrum som origo, blir den kanoniske formen
I dette koordinatsystemet ligger brennpunktene i og i . Avstanden mellom sentrum og det ene brennpunktet blir kalt lineær eksentrisitet.[trenger referanse]
Kanonisk form for hyperbelen[rediger | rediger kilde]

For hyperbelen eksisterer det tre kanoniske former, én med origo i det ene brennpunktet og to med origo i sentrum.[23] Som for en ellipse er sentrum definert som midtpunktet mellom de to brennpunktene.
Med origo i det ene brennpunktet er standardformen gitt som
I analogi med ellipsen definerer en også for hyperbelen to halvakser, der den største halvaksen er halve korden gjennom sentrum som forbinder to punkt på de to hyperbelgrenene. Parameteren er lengden av denne halvaksen. Toppunktene på de to grenene er gitt ved . Helt tilsvarende som for ellipsen har en sammenhengen
Brennpunktene ligger i og . Direktrisen svarende til det første brennpunktet skjærer -aksen i , forutsatt at er større enn null.
Med origo i sentrum mellom brennpunktene er standardformen gitt som
Brennpunktene ligger nå i og i . Hyperbelen har asymptotene . Toppunktet til hyperbelen på den positive -aksen ligger på , og det følger at parameteren er lik lengden av halve den korden mellom asymptotene som tangerer hyperbelen i toppunktet.
En hyperbel kalles ekvilateral eller likesidet dersom . Siden asymptotene i dette tilfellet står vinkelrett på hverandre, kalles hyperbelen i dette tilfelle også rektangulær. For en likesidet hyperbel brukes også en standardform som en får ved å rotere aksesystemet 45 grader:
Her er .
Kjeglesnittparametre fra standardformer[rediger | rediger kilde]
Tabellen under gir en oppsummering av kjeglesnittparametre fra vanlige standardformer. Som før er
- a og b lengder av store og lille halvakse
- c lineær eksentrisitet
- e eksentrisiteten
- h avstanden mellom brennpunkt og direktrise
- p semi-latus rectum
| Kjeglesnitt | Ligning | e | c | p | h | Brennpunkter | Direktriser |
|---|---|---|---|---|---|---|---|
| Sirkel | |||||||
| Ellipse | |||||||
| Parabel | |||||||
| Hyperbel |
Standardligninger på parametrisk form[rediger | rediger kilde]
Samtlige av kurvene på standardform kan uttrykkes som en parameterfremstilling. Parabelen med toppunkt i origo er gitt ved
Ellipsen med sentrum i origo er gitt ved
Hyperbelgrenen med positive -verdier er definert ved
Ordliste for kjeglesnitt[rediger | rediger kilde]

Det følgende er en liten oversikt over den rik terminologien knyttet til kjeglesnitt:
- Brennpunkt eller fokus: Punkt brukt sammen med en styrelinje til å definere et kjeglesnitt som et geometriske sted.
- Degenerert kjeglesnitt: Skjæringslinjen mellom en kjegleflate og et plan når planet går gjennom toppunktet i kjeglen; et punkt, én linje eller to linjer.
- Diameter: Korde mellom to punkt på kjeglesnittet, gjennom sentrum (for ellipsen og hyperbelen)
- Diskriminant: Algebraisk kombinasjon av koeffisientene i en kvadratisk ligning, brukt til å skille om ligningen framstiller en hyperbel, parabel eller ellipse
- Eksentrisitet: Mål for hvor langt et kjeglesnitt avviker fra en sirkel.
- Gren: Hver av de to delene i en hyperbel.
- Homofokal eller konfokal: To kjeglesnitt er homofokale eller konfokale dersom de har samme brennpunkt.
- Kanonisk form eller standardform: Form for ligningen til et kjeglesnitt som presenterer kurven på en enkel måte.
- Konjugerte diametre: To diametre er konjugerte dersom enhver korde parallell med den ene diameteren blir delt i to like deler av den andre.[24] De to aksene i en ellipse og en hyperbel er også konjugerte.
- Latus rectum: Korden mellom to punkt i et kjeglesnitt, gjennom brennpunktet.
- Likesidet, ekvilateral eller rektangulær hyperbel: Hyperbel der .
- Lille akse: I en ellipse og hyperbel, en akse konjugert til den store aksen.
- Semi-latus rectum: Halve korden mellom to punkt i et kjeglesnitt, gjennom brennpunktet.
- Sentrum: Midtpunktet mellom brennpunktene i en ellipse og en hyperbel.
- Sentralt kjeglesnitt: Kjeglesnitt som er symmetrisk om et sentrum, det vil si ellipse eller hyperbel.[25]
- Store akse: I en ellipse og hyperbel, korden gjennom brennpunktene og normal til styrelinjen.
- Styrelinje eller direktrise: Rett linje brukt sammen med et brennpunkt til å definere et kjeglesnitt som et geometriske sted.
- Toppunkt eller vertex: Ekstremalpunkt i et kjeglesnitt, i standardformer skjæringspunkt mellom en akse og kjeglesnittet.
- Transvers akse: I en hyperbel aksen gjennom brennpunktene, altså den store aksen.
Kjeglesnitt som kvadratisk form[rediger | rediger kilde]

En generell kvadratisk ligning i to variable med reelle koeffisienter vil alltid fremstille et kjeglesnitt, degenerert eller ikke-degenerert:
Funksjonen er en kvadratisk form, et polynom i to variable av grad to. Kjeglesnittet er en nivåkurve og også en nullmengde for funksjonen.
Diskriminanten til ligningen brukes til å bestemme typen av kjeglesnitt og er definert ved[26]
Ligningen kan overføres til en av standardformene ved en passende koordinattransformasjon, svarende til en translasjon og en rotasjon.
Ligningen på matriseform[rediger | rediger kilde]
Ved hjelp av matriser kan ligningen skrives på formen
Determinanten til matrisen er proporsjonal med diskriminanten:
Begge disse størrelsene er invariante under vilkårlige rotasjoner og translasjoner. Det samme gjelder sporet til matrisen . som er lik .
Ved hjelp av en 33-matrise kan ligningen også skrives som
Determinanten til matrisen er viktig når en skal bestemme typen kjeglesnitt:
Også denne determinanten er invariant under vilkårlige rotasjoner og translasjoner.
Kurveklassifikasjon[rediger | rediger kilde]
Typen kjeglesnitt kan bestemmes ved hjelp av diskriminanten til andregradsligningen:[26]
- En ellipse når .
- En parabel når .
- En hyperbel når .
Siden determinanten til en matrise alltid er lik produktet av egenverdiene, og , så kan også fortegnet til egenverdiene til matrisen brukes tilsvarende som diskrimnanten:
- En ellipse når egenverdiene har samme fortegn.
- En parabel når en av egenverdiene er lik null.
- En hyperbel når egenverdiene har ulike fortegn.
Kjeglesnittet vil være degenerert når determinanten er lik null. En fullstendig klassifikasjon er gitt ved følgende skjema:[23]
| Diskriminant | Determinant | Kjeglesnitt | ||
|---|---|---|---|---|
| Parabel | ||||
| To parallelle reelle linjer | ||||
| To parallelle sammenfallende linjer | ||||
| To parallelle imaginære linjer | ||||
| To parallelle reelle linjer | ||||
| To parallelle sammenfallende linjer | ||||
| To parallelle imaginære linjer | ||||
| Ellipse | ||||
| Punkt-ellipse | ||||
| Hyperbel | ||||
| To kryssende linjer |
Overføring til standardform[rediger | rediger kilde]
For ikke-degenerert ellipser og hyperbler, der er ulik null, kan en overføre den generelle ligningen til standardform ved hjelp av egenverdiene til matrisen :[27]
Denne ligningen er ekvivalent med formen
De to egenverdiene er og . Ligningen fremstiller en ellipse når de to egenverdiene har samme fortegn og en hyperbel ellers.
Eksentrisitet[rediger | rediger kilde]
For en parabel er eksentrisiteten lik 1. For en ellipse og en hyperbel kan eksentrisiteten uttrykkes ved koeffisientene:[28]
Her er koeffisienten lik 1 dersom determinanten er negativ og lik -1 når determinanten er positiv.
Hovedakser og sentrum[rediger | rediger kilde]
For en vilkårlig ikke-degenerert ellipse eller hyperbel kan en uttrykke hovedakser og sentrum ved hjelp av ligningskoeffisientene. Senteret har koordinater gitt ved[trenger referanse]
Vinkelen mellom den store aksen og den positive -aksen er gitt ved[trenger referanse]:
Overføringen til standardform utført i foregående avsnitt viser også at halvaksene er gitt ved
Tangentlinjer[rediger | rediger kilde]
Ligningen for en tangentlinje til en nivåkurve for funksjonen i punktet er generelt gitt ved[29]
Her er og partiell deriverte med hensyn på henholdsvis og . For et kjeglesnitt på formen gir dette tangentligningen
Tangentligningen knyttet til standardformen for ellipser og hyperbler med origo i sentrum er dermed
For en parabel på standardformen med sentrum i toppunktet er tangentligningen
Kjeglesnitt i projektiv geometri[rediger | rediger kilde]
I projektiv geometri blir beskrivelsen av kjeglesnitt enklere og mer systematisk. En ellipse kan da beskrives som et kjeglesnitt som ikke skjærer linjen i det uendelig fjerne. Parabelen vil også være en lukket kurve som tangerer denne linjen i ett dobbeltpunkt, mens en hyperbel skjærer den i to forskjellige punkt gitt ved retningene til de to asymptotene. Ved projektive transformasjoner kan disse kjeglesnittene omformes i hverandre ved at de flyttes i forhold til linjen i det uendelige fjerne.
I denne beskrivelsen blir også hyperbelen en lukket kurve. Beveger man seg mot uendelig langs en gren, vil man passere linjen i det uendelige langs en asymptote, dukke opp igjen på motsatt side av samme asymptote slik at man kommer tilbake på den andre grenen av hyperbelen. Følger man denne grenen videre, forsvinner man igjen langs den andre asymptoten og dukker så opp igjen på den grenen hvor man startet etter å ha passert linjen i det uendelige enda en gang. Slik kan hyperbler ses som ellipser som har blitt trukket gjennom uendelig og gjenoppstår på den andre siden.
Pol og polare[rediger | rediger kilde]
En pol og en polare for et kjeglesnitt er i projektiv geometri henholdsvis et punkt og en linje som har et gjensidig forhold til hverandre, relativt til kjeglesnittet. For et gitt punkt (polen) kan en beregne posisjonen til den rette linjen (polaren). Har en omvendt gitt en rett linje (polaren), så er posisjonen til punktet (polen) gitt.
Komplekse koordinater[rediger | rediger kilde]
I den projektive beskrivelsen kan koordinatene ha komplekse verdier. Dette er en naturlig generalisering i moderne matematikk. Det vil da ikke lenger være noen forskjeller mellom ellipser og hyperbler. For eksempel, så vil sirkelen x2 + y2 = 1 gå over til hyperbelen x2 - y2 = 1 ved å la y → iy hvor i er den imaginære enheten. Ellipsen og hyperbelen vil da kunne klassifiseres som tilhørende samme type kjeglesnitt. Mens hyperbelen har to reelle skjæringspunkt med linjen i det uendelige, vil ellipsen ha to komplekse skjæringspunkt. En parabel tilsvarer da spesialtilfellet hvor disse to skjæringspunktene faller sammen til ett, og man har en tangering i stedet.
Referanser[rediger | rediger kilde]
- ^ a b c : G. Thomas, R. Finney; Calculus and Analytic Geometry s.432
- ^ : C.B.Boyer; A history of mathematics s.107f
- ^ : T. Heath; A History of Greek Mathematics I s.244ff
- ^ a b : T. Heath; A History of Greek Mathematics I s.438
- ^ a b : T. Heath; A History of Greek Mathematics II s.110ff
- ^ : C.B.Boyer; A history of mathematics s.205ff
- ^ : T. Heath; A History of Greek Mathematics II s.541f
- ^ a b : C.B.Boyer; A history of mathematics s.249ff
- ^ «Ibn Al-Haytham, Abū» (engelsk). encyclopedia.com. 1. desember 2019. Besøkt 13. januar 2020.
- ^ : C.B.Boyer; A history of mathematics s.322ff
- ^ : F.J Swetz; The European Mathematical Awakening s.101
- ^ : F.J Swetz; The European Mathematical Awakening s.133
- ^ : C.B.Boyer; A history of mathematics s.354ff
- ^ : S. Schwartzman; The Words of Mathematics... s.95
- ^ «Small bodies: Profile» (engelsk). NASA. Besøkt 13. januar 2020.
- ^ : F.J Swetz; The European Mathematical Awakening s.166f
- ^ a b : C.B.Boyer; A history of mathematics s.393ff
- ^ Morten Eide (20. januar 2013). «Geometrisk morfologi - forvandlinger av en kjeglesnittype» (PDF). morphomatic.org. Besøkt 16. januar 2020.
- ^ : C.B.Boyer; A history of mathematics s.572
- ^ a b : C.B.Boyer; A history of mathematics s.408
- ^ : S. Schwartzman; The Words of Mathematics... s.75
- ^ Andrew Bashelor, Amy Ksir og Will Traves (2008). «Enumerative Algebraic Geometry of Conics» (PDF). Amer. Math. Monthly. 115 (6): 701–728.
- ^ a b c d e f : J.D. Lawrence; A Catalog of Special Plane Curves s.61ff
- ^ Barry Spain (1957). Analytical Conics. New York: Pergamon Press. s.39ff
- ^ «Central Conic» (engelsk). The Concise Oxford Dictionary of Mathematics. Besøkt 16. januar 2020.
- ^ a b : G. Thomas, R. Finney; Calculus and Analytic Geometry s.430
- ^ Ayoub B. Ayoub (1993). «The Central Conic Sections Revisited». Mathematics Magazine. 66 (5): 322–325. JSTOR 2690513.
- ^ Ayoub B. Ayoub (2003). «The Eccentricity of a Conic Section». The College Mathematics Journal. 34 (2): 116–121. JSTOR 3595784.
- ^ T.M. Apostol (1969). Calculus. II. New York: John Wiley & Sons. s. 62. ISBN 0-471-00008-6. s.268
Litteratur[rediger | rediger kilde]
- T. M. Apostol, A First Course with Applications to Differential Equations, John Wiley & Sons, New York (1997). ISBN 0-471-17421-1.
- Carl B. Boyer (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
- Thomas Heath (1981). A History of Greek Mathematics. I. New York: Dover Publications. ISBN 0-486-24073-8.
- Thomas Heath (1981). A History of Greek Mathematics. II. New York: Dover Publications. ISBN 0-486-24074-6.
- J.Dennis Lawrence (1972). A Catalog of Special Plane Curves. Mineola, New York: Dover Publications. ISBN 978-0-486-60288-2.
- Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9.
- Frank J. Swetz, red. (2013). The European Mathematical Awakening. Mineola, New York: Dover Publications. ISBN 0-486-49805-0.
- A. Søgaard og R. Tambs Lyche, Matematikk for den høgre skolen, vol III, Gyldendal Norsk Forlag, Oslo (1955).
- George B. Thomas, Ross L. Finney (1995). Calculus and Analytic Geometry (9th edition utg.). Reading, USA: Addison-Wesley. ISBN 0-201-53174-7.
Galleri[rediger | rediger kilde]
-
Ilustrasjon av kjeglesnitt fra det leksikalske verket Cyclopaedia (1728)
-
Kjeglesnitt med felles brennpunkt, styrelinje og latus rectum
-
Ellipseterminologi
-
Hyperbelterminologi
-
Parabelterminologi
Eksterne lenker[rediger | rediger kilde]
- J. Gut, Kegelschnitte, myk innføring på tysk.
- J.A. Christophersen og K. Ranestad, Geometri - MAT 2500, forelesninger ved Universitetet i Oslo (2014).






















![{\displaystyle {\begin{alignedat}{2}&0^{\circ }\leq \theta <\phi \qquad &&{\text{Hyperbel}}\\[3pt]&\theta =\phi \qquad &&{\text{Parabel}}\\[3pt]&\phi <\theta \leq 90^{\circ }\qquad &&{\text{Ellipse}}\\[3pt]&\theta =90^{\circ }\qquad &&{\text{Sirkel}}\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9445d2bd21019ad860f34e0b6a10681d6fa1c91a)
































![{\displaystyle {\begin{alignedat}{2}g&={\frac {p}{1+e}}=a(1-e)\\[3pt]a&={\frac {p}{1-e^{2}}}\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64e50ee41c89af7c831b7cf1ecb716c1ef516561)

![{\displaystyle {\begin{alignedat}{2}p^{2}&=[y(x=0)]^{2}=b^{2}(1-e^{2})\\[3pt]b^{2}&={\frac {p^{2}}{1-e^{2}}}=ap\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9f9503f9509335bfe9511edbf6465996a95ed3c)






![{\displaystyle {\begin{alignedat}{2}g&={\frac {p}{1+e}}=a(e-1)\\[3pt]a&={\frac {p}{e^{2}-1}}\\[6pt]p^{2}&=[y(x=0)]^{2}=b^{2}(e^{2}-1)\\[3pt]b^{2}&={\frac {p^{2}}{e^{2}-1}}=ap\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18c03d8ef5be5b369ece8b46cea3c4bec108887f)


































![{\displaystyle {\begin{alignedat}{2}{\mathsf {x}}&=(x,y)\\[3pt]{\mathsf {M}}&=\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\\[3pt]{\mathsf {N}}&=\left({\begin{matrix}D&E\end{matrix}}\right)\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed91f7a0157121d7d97a3452ea976c75d5f26929)






![{\displaystyle {\begin{alignedat}{2}{\mathsf {x}}&=(x,y,1)\\[3pt]{\mathsf {R}}&=\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\\[3pt]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d55366296d3d5f70666d08b3e670e26ef2915c)







































