Kurve
En kurve i matematikk kan beskrives som et endimensjonalt geometrisk objekt, en kontinuerlig samling av punkt i det reelle rommet Rn eller i det komplekse rommet Cn. Kurven kan betraktes som banen til et punkt som beveger seg. Kurven har lengde, men ikke bredde eller dybde. Krav til en generell formell definisjon av en kurve har vært omdiskutert gjennom historien.
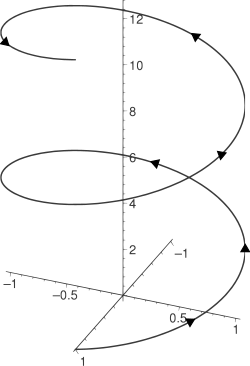
Kurver har mange anvendelsesområder, både i matematikk og i andre fagområder. Studiet av kurver inngår i mange deler av matematikk, slik som i matematisk analyse, i geometri og i topologi. En lang rekke kurver har egne navn, og figuren til venstre viser en skrulinje, også kalt en heliks.
En kurve i det tre-dimensjonale rommet kan lokalt karakteriseres ved en tangentretning, en krumning og en torsjon. Tangenten er en vektor som peker i retningen langs kurven. Krumningen indikerer hvor fort tangentretningen endrer seg. Torsjonen er et mål på om kurven er plan eller om den vrir seg ut av et plan. Sammenhengen mellom tangent, krumning og torsjon er gitt ved Frenets formler, også kalt Frenet-Serrets formler.
Begrepet linje blir av og til brukt synonymt med en kurve (krum linje), av og til synonymt med en rett linje. En rett linje er et spesialtilfelle av en kurve. Ordet «kurve» stammer fra det latinske curvus, med betydning «bøyd» eller «krummet».[1]
For reelle funksjoner blir ordet kurve også brukt synonymt med grafen til funksjonen. Denne bruken er også reflektert i sammensetninger som «glemselskurve» og «feberkurve».
Formell definisjon[rediger | rediger kilde]
Formelle definisjoner av en kurve tar utgangspunkt i en funksjon fra et reelt intervall inn i et rom :
Hvilke krav som må stilles til funksjonen og rommet har vært omdiskutert i matematikkens historie varierer og vil variere i ulike presentasjoner.[2] Også hvilket element som refereres til som kurve har variert: I noen definisjoner sies kurven å være verdimengden til [3], mens andre refererer til funksjonen som kurven[4]. I det siste tilfelle kan ulike kurver ha samme punktmengde. I topologi kan det også forekomme at intervallet blir omtalt som en kurve.[2]
For grunnleggende studier av kurver vil være det todimensjonale planet R2 eller det tredimensjonale rommet R3, og et vanlig krav er da at er en kontinuerlig funksjon.[3][4] For å kunne bruke teori fra differensialgeometri er det også vanlig å anta at funksjonen er stykkevis kontinuerlig deriverbar.
Et strengt krav om kontinuitet vil ekskludere fra definisjonen kurver som består av adskilte deler, slik som for eksempel hyperbelen. I vanlig språkbruk refererer en også til en endelig union av adskilte kurver som en kurve.[3] En vilkårlig kontinuerlig del av en kurve kan kalles en bue.[5]
Også for mer generelle definisjoner, der rommet er en topologi, var det lenge ansett som tilstrekkelig at funksjonen er kontinuerlig, for å definere det vi intuituvt forstår med en kurve.[2] I 1890 ga den italienske matematikeren Giuseppe Peano imidlertid et eksempel på en kontinuerlig surjektiv funksjon , det vil si en funksjon der verdimengden fyller et helt todimensjonalt område. For å unngå slike patologiske kurver kan en innføre ulike tilleggsvilkår på funksjonen og rommet .
Definisjon av kurver i det euklidske rommet[rediger | rediger kilde]
En kurve i det euklidske rommet R3 kan kalles en romkurve, mens en plan kurve ligger fullt og helt i et plan.[6] Alle kurver i R2 er plane kurver, inkludert kurven definert ved grafen til en reell funksjon av en variabel.
Parameterfremstilling[rediger | rediger kilde]
En romkurve kan beskrives ved hjelp av en parameterfremstilling, også kalt parametrisering, på forma[7]
Parameterområdet T er et intervall i R. En alternativ skriveform er
Dersom en av disse funksjonene er lik null, så er kurven plan.[8]
Et eksempel på en parameterfremstilling er gitt ved definisjonen for en heliks med akse langs -aksen:
Her er og størrelser som styrer forma på heliksen.
Det vil alltid eksistere mange valg av parametriseringer for en gitt kurve. Parameteren kan for eksempel representere tiden som går når et punkt beveger seg langs kurven eller beskrive avstanden langs kurven fra et gitt startpunkt.
Punkt der deriverte av , og med hensyn på samtidig er lik null kalles singulære punkt. Alle andre punkt er regulære punkt.
Implisitt definisjon[rediger | rediger kilde]
En kurve i planet i kan defineres eksplisitt som grafen til en funksjon eller implisitt ved en enkelt ligning av typen
En romkurve kan defineres implisitt ved hjelp av to ligninger
Hver av ligningene definerer en flate i rommet, og kurven er dermed definert som samlingen av punkt som ligger på begge flatene, det vil si langs skjæringslinjen mellom flatene. Da to flater kan ha flere adskilte skjæringslinjer, trenger ikke en implisitt definisjon være entydig.
Naturlige ligninger og fundamentalteoremet for romkurver[rediger | rediger kilde]
En kurvedefinisjon basert på en parameterframstilling eller en implisitt formulering vil generelt være avhengig av det valgte koordinatsystemet. Alternativt kan en kurve defineres på en måte som er uavhengig av koordinatsystemet, ved å spesifisere krumning og torsjon til kurven. Se avsnitt under for definisjon av disse to størrelsene. Ved å spesifisere krumning og torsjon som funksjon av buelengden vil en kurve være entydig bestemt, bort sett fra startpunktet og orientering i rommet. Dette er formulert i det såkalte fundamentalteoremet for romkurver:[9]
Gitt to vilkårlige kontinuerlige funksjoner og , der er positiv. Da eksisterer det én og kun én romkurve, entydig bestemt bortsett fra posisjon og orientering i rommet, som har buelengden , krumningen og torsjon lik En plan kurve har null torsjon og er derfor entydig gitt ved funksjonen .
Ligningene og kalles de naturlige ligningene til romkurven.
En heliks er definert som en kurve med konstant positiv krumning og torsjon. En klotoide er en plan kurve der krumningen endrer seg lineært med buelengden.
Geometrisk definisjon[rediger | rediger kilde]
En kurve kan defineres geometrisk, for eksempel kan en ellipse defineres som det geometriske sted for et punkt der avstanden til to definerte punkt har en gitt konstant sum. En romkurve kan også defineres som en skjæringslinje mellom to flater.
Kurvetyper og egenskaper[rediger | rediger kilde]

En kurve er lukket dersom startpunktet og endepunktet er det samme. En sirkel er eksempel på en lukket kurve.
En plan, lukket kurve som ikke krysser seg selv kalles en Jordan-kurve. En slik kurve deler et plan i en innside og en utside, et resultat som er formulert i Jordans kurveteorem.
En glatt kurve er en kurve der parameterfunksjonene , og alle har kontinuerlige deriverte. En glatt kurve har ingen spisse hjørner. Kurven er stykkevis glatt dersom den er glatt overalt, bortsett fra i et endelig antall punkt, der den kan ha knekkpunkt. En gren av kurven er en del mellom to påfølgende knekkpunkt. Det engelske ordet «cusp» («spydspiss») blir brukt for å betegne et knekkpunkt der tangentretningene til kurven på hver side av knekkpunktet har sammenfallende retning i grenseverdien når en nærmer seg knekkpunktet.
Kjeglesnitt[rediger | rediger kilde]
Kjeglesnitt er en familie av plane kurver som framkommer som skjæringslinjer når et plan skjærer en kjegleflate. Familien av kjeglesnitt omfatter sirkelen, ellipseen, parabelen og hyperbelen. Typen kurve avhenger av hvordan planet som snitter forholder seg til kjegleflaten.
Algebraiske kurver[rediger | rediger kilde]
En algebraisk kurve er en kurve definert implisitt som skjæringskurven mellom to algebraiske flater. Når en slik flate har grad , er definert ved en ligning , der er et polynom av grad . En kurve som ikke er algebraisk, er en transcendental kurve.
Dersom de to algebraiske flatene har grad henholdsvis m og n, så defineres graden til den algebraiske kurven å være lik produktet (mn).
Mer formelt kan en algebraisk kurve defineres som en endimensjonal varietet.[trenger referanse]
Den enkleste formen for en algebraisk kurve er en rett linje. Kjeglesnittene er algebraiske kurver av grad 2. Noen lissajouskurver er av grad 3.
Rasjonale kurver[rediger | rediger kilde]
En rasjonal kurve eller en unikursal kurve er en plan algebraisk kurve som kan defineres ved en parameterfremstilling der de to funksjonene er rasjonale, det vil si brøker av polynom i parameteren .[8]
Matematisk tilsvarer det at de er kurver med genus g = 0.[klargjør]
Alle kjeglesnitt er unikursale. En sirkel med sentrum i origo og radius 1 kan for eksempel parametriseres ved hjelp av ligningene
Hyperbelen kan parametriseres ved
Geodetiske kurver[rediger | rediger kilde]
En geodetisk kurve er en kurve som følger den korteste vei mellom to punkt på en kurvet flate.[10] På en kuleflate vil en geodetisk kurve ligge på en storsirkel.
Kurver på en kuleflate kalles generelt sfæriske kurver. Geodetiske kurver er også definert for andre flater enn kuleflater.
Buelengde og tangentvektor[rediger | rediger kilde]

Buelengden til en kurve er avstanden langs kurven fra et gitt startpunkt. Dersom kurven er gitt ved en parametrisering og startpunktet er , så er buelengden definert ved[7]
Her betyr merket den deriverte med hensyn på parameteren , det vil si .
Det er vanlig å bruke buelengden som parameter i beskrivelsen av en kurve, i det som kalles en naturlig parametrisering. Mange matematiske formler får da en enklere form.
En tangent er en rett linje som berører kurven i et punkt og som har samme gradient som kurven i punktet. En tangentvektor er definert ved uttrykket
der parameteren er buelengden. Fra definisjonen av buelengden følger det at , og tangentvektoren er derfor en enhetsvektor:
Normalvektor og krumning[rediger | rediger kilde]
Deriverer en begge sidene i ligningen resulterer dette i en ny ligning
Den deriverte av tangent med hensyn på buelengden er derfor normal eller vinkelrett til tangenten og definerer krumningsvektoren
Enhetsvektoren kalles normalvektoren eller prinsipalnormalen, og er krumningen til kurven. Fortegnet til normalen og krumningen er ikke definert ut fra ligningen, og det er mulig å bruke en definisjon der krumningen alltid er positiv. Det er også mulig å knytte et fortegn til krumningen, for å skille mellom konvekse og konkave deler, for eksempel relativt til en koordinatakse.[11]
Krumningen sier noe om hvor raskt tangentvektoren skifter retning langs kurven. Det følger fra når man benytter definisjonen av den deriverte som grensen
da tangentvektoren er en enhetsvektor, og er den lille vinkelen den dreier seg i planet normalt til over et lite veistykke .

Absoluttverdien til krumningen er gitt ved lengden til krumningsvektoren, . Den inverse verdien kalles krumningsradien,
- .
For en sirkel er denne lik sirkelradien. En rett linje har krumningsradius lik uendelig.
Prinsipalnormalen er en enhetsvektor, slik at . Ved derivasjon av dette uttrykket finner man at tangentvektoren må oppfylle
Den deriverte av normalen står altså vinkelrett på normalen.
Krumning av en plan kurve[rediger | rediger kilde]
For en plan kurve med en vilkårlig parameterfremstilling
er tangenten definert ved
Dens lengde er gitt ved den deriverte av buelengden til kurven,
Enhetstangenten finnes nå ved normalisering,
Prinsipalnormalen står normalt på denne og blir
Krumningen til kurven kan derfor beregnes fra
I det spesielle tilfellet at kurven er gitt som , forenkles uttrykket til[8]
Krumningssenter[rediger | rediger kilde]
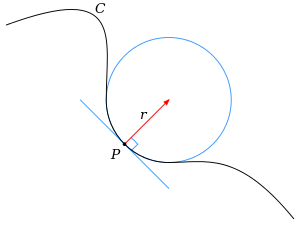
I et punkt r på kurven hvor krumningen κ er forskjellig fra null, er den konkav i en retning. Tenker man seg en sirkel på denne siden som tangerer kurven og har samme krumning som kurven, kalles denne sirkelen for kurvens krumningssirkel og dens senter for kurvens krumningssenter. Den har derfor radius ρ = 1/κ. Betegnes dette med vektoren c, er det derfor gitt ved ligningen
hvor n er kurvens normal.[8]
Fra uttrykket for krumningen til en plan kurve r = (x(t ), y(t )) er derfor koordinatene til dens krumningssenter gitt som
Når parameteren t varierer, vil krumningssenteret til kurven vanligvis flytte seg. Det beskriver en ny kurve som kalles dens evolute. Man kan vise at den er omhyllingskurven til normalene til den gitte kurven. Bare for en sirkel ligger krumningssenteret i ro, og evoluten er et punkt.[7]
Eksempel[rediger | rediger kilde]

En parabel med akse langs y-aksen er gitt ved ligningen x 2 = 2ay, der konstanten a angir formen. Man kan da velge koordinaten x som den fri parameter for kurven. Da er x' = 1 og x" = 0. Fra ligningen til parabelen vil da på samme måte y' = x/a og y" = 1/a. Koordinatene til krumningssenteret blir nå
Krumningssenteret ligger dermed på kurven
- ,
som er parabelens evolute. Evoluten har en spiss på y-aksen og kalles av enkelte forfattere for en semikubisk parabel.[12]
Torsjon og binormalvektor[rediger | rediger kilde]
Fra normalvektoren og tangenten kan en definere en tredje vektor kalt binormalvektoren til kurven,
De tre vektorene , og er alle enhetsvektorer og står normalt på hverandre. Sammen danner vektorene et bevegelig aksekors langs kurven og blir referert til som et trihedron. For å unngå forveksling med binormalen, kan en også bruke navnet hovednormal om normalen .
Planet gjennom tangentvektoren og normalvektoren kalles oskulasjonsplanet eller smygplanet. Det kan betraktes som et plan gjennom tre påfølgende punkt på kurven.

Da binormalen er en enhetsvektor, vil produktet være konstant lik 1 langs kurven. Ved derivasjon av ligningen følger det at den deriverte av binormalen må oppfylle . Binormalen står samtidig vinkelrett på tangenten, slik at . Derivasjon av dette kravet gir at , når man benytter at . Vektoren står derfor vinkelrett både på binormalen og på tangenten og må ha samme retning som normalen . Dermed kan man skrive
hvor koeffisienten kalles torsjonen til kurven. Den er et mål for hvor raskt oskulasjonsplanet dreier seg langs kurven. I motsetning til krumningen, er fortegnet til torsjonen entydig bestemt, og torsjonen kan være både positiv og negativ.[13].
En kurve er plan hvis og bare hvis den har torsjon lik null. Da er binormalen en konstant vektor, oskulasjonsplanet er det samme langs hele kurven, og kurven ligger fullt og helt i dette planet.
Frenets formler[rediger | rediger kilde]
Variasjonen av normalen langs kurven er gitt ved den deriverte
Her er benyttet uttrykkene for deriverte av tangenten og binormalen samt relasjonen mellom de tre vektorene i trihedronet.
De tre ligningene som beskriver hvordan vektorene , og varierer langs kurven, kalles for Frenets formler[7]. Ligningene kan sammenfattes slik
Alternativt blir også navnet Frenet-Serrets formler benyttet, oppkalt etter de to franske matematikerne Jean Frédéric Frenet og Joseph Alfred Serret.
Totalkrumning[rediger | rediger kilde]
Torsjon kan også omtales som en type krumning, og krumningen og torsjonen kalles av enkelte forfattere for henholdsvis første og andre krumning.[14] Størrelsen
omtales også som tredje krumning eller totalkrumning.[7][14] Fra Frenets formler ser en at denne svarer til lengden av den deriverte av hovednormalen, og totalkrumningen er et mål for hvor raskt normalen endrer seg langs kurven.
En plan kurve kan ha krumning, mens både torsjon og totalkrumning er uttrykk for krumning i rommet. For en plan kurve der torsjonen er null, er totalkrumningen lik krumningen κ.
Navnet totalkrumning brukes også om et integral av krumningen med hensyn på buelengden.[trenger referanse]
Eksempler[rediger | rediger kilde]
Heliks[rediger | rediger kilde]
Et punkt på en heliks er gitt ved posisjonsvektoren
der og er positive koeffisienter. Derivasjon av posisjonsvektoren gir
som viser at buelengden øker proporsjonalt med parameteren t da er konstant. Enhets-tangentvektoren er dermed gitt ved
Prinsipalnormalen til kurven finnes fra den deriverte av tangenten
slik at normalen er
Videre er krumningen gitt ved
som er konstant langs kurven. Binormalen kan bestemmes fra kryssproduktet
Den deriverte av binormalen er gitt ved
For torsjonen gir dette
som viser at den også er konstant. I grensen er torsjonen null, og heliksen har degenerert til en sirkel.
Partikkelbaner[rediger | rediger kilde]
Et materielt punkt er et legeme som er slik at posisjonen kan beskrives ved hjelp av ett enkelt punkt i et koordinatsystem.[15] Dersom et slikt punkt eller partikkel beveger seg, vil posisjonen være en funksjon av tiden :
Partikkelbanen kalles også trajektorien til det materielle punktet. Fra partikkelbanen kan en utlede grunnleggende egenskaper til bevegelsen. Den vektorielle hastigheten er tangent til trajektorien:
Her er brukt en vanlig konvensjon med at et prikk over en størrelse betegner derivasjon med hensyn på tiden. Den skalare størrelsen er farten. Både den og tangentvektoren vil i alminnelighet variere under bevegelsen. Akselerasjonen er definert som den tidsderiverte av hastigheten:
Ved å bruke Frenets første ligning , har man dermed for akselerasjonen
I denne sammenhengen er det vanlig å definere krumningen som alltid positiv, slik at den kan erstattes med krumningsradien :
Akselerasjonen består av to komponenter, en komponent langs tangenten til partikkelbanen og en komponent langs hovednormalen. Komponenten langs tangenten avhenger av tidsendringen i farten og kalles tangentialakselerasjonen. Komponenten langs hovednormalen er sentripetalakselerasjonen og skyldes at bevegelsen skifter retning. For en ren sirkelbevegelse med konstant hastighet er tangentialakselerasjonen lik null, og kun sentripetalakselerasjonen bidrar.[8]
Historie[rediger | rediger kilde]
Interessen for kurver og geometriske oppsto lenge før de ble objekter for systematisk matematisk behandling. Kurver ble brukt til dekorasjon av potter og andre gjenstander langt tilbake i oldtiden. Den rette linjen og sirkelen har vært kjent like lenge som vi har skriftlige kilder.
Grekeren Hippias levde i det femtre århundre, på samme tid som Sokrates, og er kjent som den første til å beskrive en kurve utenom den rette linjen og sirkelen.[16] Kurven ble brukt til å løse problemet med vinkelens tredeling og ble derfor tidligere kalt trisektrisen til Hippias, men kalles i dag en kvadratrise. Kjeglesnittene ellipse, hyperbel og parabel ble først beskrevet av Menaikhmos (født ca 360 f.Kr.)[17]
Euklid (født ca 300 f.Kr.) definerte i læreverket Elementer en linje som «en lengde uten bredde», men uttrykket hadde antagelig oppstått før Euklid, i Platons skole.
Arkimedes (født ca 287 f.Kr.) regnes som en av de viktigste vitenskapsmennene i antikken og også som en grunnlegger av matematisk fysikk. I læreverket Om spiraler studerer han en spiral i planet, definert som banen til et punkt som beveger seg med konstant fart langs en stråle, samtidig som strålen roterer med konstant fart. Her beskriver han også et konsept tilsvarende det vi i dag kaller tangenten til kurven. Arkimedes gir æren til vennen Konon fra Aleksandria for å ha introdusert spiralen. Motivasjonen bak studiet av kurven var tredelingen av vinkelen og også sirkelens kvadratur.
Arkimedes kan ha innført begrepet «parabel», i et verk som er kalt Kvadrering av parabelen, men det er uvisst om originalversjonen brukte dette ordet. Her bestemmer Arkimedes arealet under et segment av en parabel, ved å dele arealet opp i trekanter. Apollonios fra Perge (født 262 f.Kr.) brukte alle de tre ordene ellipse, hyperbel og parabel i boka Kjeglesnitt. Her viser han at alle tre typer kurver vil opptre når et plan skjærer en rett kjegle, ved å variere helningen på planet. Han innførte også bruken av en dobbelt kjegle, slik at kurvene kan få to adskilte greiner.
Romerne brukte ordet «linea» om en tråd spunnet av lin.[1] Siden en tråd kan anta alle slags former, så ble ordet også brukt om det vi i dag kaller en kurve. Begrepene «rett linje» og «bøyd linje» ble brukt for å skille ulike former, der «curvus» er latin for «bøyd».
Mye av gresk matematikk gikk i glemmeboken i Europa, men ble reddet at matematikere fra Arabia og Persia. Oversettinger fra arbisk til latin førte igjen gresk kunnskap til Europa. Fire utgaver Kjeglesnitt av Appolonius hadde likevel overlevd, og en utgave ble trykket i Venezia i 1537.[18]
Innføringen av koordinater og analytisk geometri av René Descartes i det syttende århundre skapte grunnlaget for den moderne beskrivelsen av kurver.
Liste over kurver[rediger | rediger kilde]
- Bézier-kurve
- Ellipse
- Heliks
- Hyperbel
- Kjedelinje
- Klotoide
- Kvadratrise
- Lemniskate
- Parabel
- Sirkel
- Spiral
- Spline
- Superellipse
- Sykloide
- Traktrise
Referanser[rediger | rediger kilde]
- ^ a b Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9.
- ^ a b c John G. Hocking, Gail S. Young (1988). Topology. Dover Publications. ISBN 0-486-65676-4.
- ^ a b c Hans-Fredrik Aas (1974). Forelesningsreferater i matematisk analyse. II. Bergen: Matematisk institutt, Universitetet i Bergen.
- ^ a b Walter Rudin (1976). Principles of mathematical analysis. Singapore: McGraw-Hill Book Company. ISBN 0-07-085613-3.
- ^ E.J.Borowski, J.M.Borwein (1989). Dictionary of mathematics. Glasgow: Collins. ISBN 0-00-434347-6. Arc
- ^ D.J. Struik: Lectures on classical differential geometry, s.12
- ^ a b c d e R. Tambs Lyche (1961). Matematisk Analyse, Bind II. Oslo: Gyldendal Norsk Forlag.
- ^ a b c d e R. Tambs Lyche (1961). Matematisk Analyse, Bind I. Oslo: Gyldendal Norsk Forlag.
- ^ D.J. Struik: Lectures on classical differential geometry, s.29
- ^ D.J. Struik: Lectures on classical differential geometry, s.127ff
- ^ D.J. Struik: Lectures on classical differential geometry, s.15
- ^ J.D. Lawrence, A catalog of special plane curves, Dover Publications, New York (1972). ISBN 0-486-60288-5.
- ^ D.J. Struik: Lectures on classical differential geometry, s.16
- ^ a b D.J. Struik: Lectures on classical differential geometry, s.26
- ^ Oddvar Bjørgum (1963). Dynamikk. Bergen. s. 1ff.
- ^ C.B. Boyer: A history of mathematics, s.75f
- ^ C.B. Boyer: A history of mathematics, s.103f
- ^ C.B. Boyer: A history of mathematics, s.330
Litteratur[rediger | rediger kilde]
- D.J. Struik (1961). Lectures on classical differential geometry. New York: Dover Publications. ISBN 0-486-65609-8.
- C.B.Boyer (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
Eksterne lenker[rediger | rediger kilde]
- www.2dcurves.com Inneholder oversikt over nesten tusen plane kurver (Engelsk). Besøkt 7. desember 2019.
- mathshistory.st-andrews.ac.uk Oversikt og historie for en del kjente kurver (Engelsk). Besøkt 7. desember 2019.





![{\displaystyle F:[0,1]\rightarrow [0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/452dc32a29ec4ff585367207200f95f5d9a215fc)







































































![{\displaystyle {\begin{alignedat}{2}{\frac {d\mathbf {t} }{ds}}&=\kappa \mathbf {n} \\[5pt]{\frac {d\mathbf {n} }{ds}}&=-\kappa \mathbf {t} +\tau \mathbf {b} \\[5pt]{\frac {d\mathbf {b} }{ds}}&=-\tau \mathbf {n} \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e45eacf63cb9ccc2d6f3b29720206c14ae2c3f59)



















