Polynom
Et polynom er i matematikk en sum av et endelig antall ledd der hvert ledd er en konstant multiplisert med en eller flere variabler opphøyd i positive heltallseksponenter. Polynomet er definert kun ved hjelp av operasjonene addisjon, subtraksjon og multiplikasjon. I de følgende eksemplene er det vist et polynom i én variabel og et polynom i to variabler og :
Konstantene som inngår kalles også koeffisienter i polynomet.
Første del av navnet polynom kommer fra gresk polus som betyr flere. Det er uklart om andre del er avledet fra gresk nomos = regler eller latin nomen = navn. Et polynom med kun ett ledd kan kalles et monom (f.eks. ), mens et binom (f.eks. ) og et trinom (f.eks. ) har henholdsvis to og tre ledd.
Ligninger som involverer kun polynom kalles polynomligninger, og andregradsligningen er et velkjent eksempel. Funksjoner definert ved et polynom kalles naturlig nok polynomfunksjoner.
Polynom har et stort bruksområde i matematikk, og polynom opptrer i nær sagt alle fagområder der matematikk brukes. Studiet av polynomligninger og røttene har tradisjonelt vært en viktig del av algebra. Den enkle forma gjør at polynom ofte brukes for å gi en tilnærmet riktig beskrivelse av mer komplekse sammenhenger. Polynom er viktige i mange numeriske beregningsmetoder, for eksempel endelig-element-metoden.
Fundamentale begrep
[rediger | rediger kilde]Et ledd i et polynom har grad dersom summen av eksponentene til variablene i leddet er lik . Graden til polynomet er lik den største graden til samtlige av leddene. Det første eksempelet i introduksjonen har dermed grad lik tre, mens det andre har grad fire. Et polynom av grad 2 kalles både et andregradspolynom og et kvadratisk polynom, mens et kubisk polynom har grad 3.
Et polynom av grad er komplett dersom det inneholder ledd av samtlige potenser mindre eller lik i variablene. Et komplett tredjegrads polynom i én variabel har fire ledd, mens et komplett tredjegrads polynom i to variable har 10 ledd, som i det følgende eksempelet:
Et -te-grads polynom i én variabel er monisk dersom koeffisienten foran leddet med eksponent er lik 1.
Et polynom i flere variable er symmetrisk dersom en permutasjon av variablene ikke endrer polynomet. Et polynom i to variable er altså symmetrisk dersom
Et polynom i flere variable er homogent i grad dersom alle leddene har grad .
Polynomfunksjoner
[rediger | rediger kilde]
En polynomfunksjon er en funksjon som evaluerer verdien av et polynom. Begrepene polynom og polynomfunksjon blir ofte brukt om hverandre, men i abstrakt algebra er forskjellen mellom disse begrepene viktig.
Polynomfunksjoner har mange attraktive matematiske egenskaper, de er blant annet kontinuerlige og glatte. Polynom er både deriverbare og integrerbare, og resultatet av disse operasjonene er også polynom.
Polynomfunksjoner i én variabel
[rediger | rediger kilde]Den generelle forma for et -te-grads polynom i én variabel er
Her er koeffisientene i polynomet, og er argumentet i funksjonen. Eksponenten n er et naturlig tall, det vil si et positivt heltall.
Polynomfunksjoner kan være reelle eller komplekse, alt etter hvordan koeffisientene og variablene er definerte.
Horners regel eller Horner-algoritmen er en effektiv måte for beregning av polynomfunksjoner.
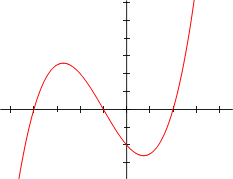
Grafen til en polynomfunksjon av grad én er en rett linje. Andregradspolynomet har en graf som blir kalt en parabel. Eksempel på polynom-grafer er vist under.
 |
 |
 |
 |
Vektorrom av polynomfunksjoner
[rediger | rediger kilde]Summen av to polynom er også et polynom. Multipliserer en et polynom med et reelt eller et komplekst tall, så er resultatet også et polynom. Tilsammen gjør dette at en kan definere en rekke vektorrom dannet fra en basis av polynomfunksjoner. Som en del av definisjonen inngår også det såkalte nullpolynomet, definert ved
Som et eksempel kan en definere basisfunksjonene
Et vilkårlig -te-grads polynom kan da skrives som
Koordinatvektoren er gitt ved
Vektorrommet av polynom opp til grad er et -dimensjonalt vektorrom med samme struktur som , det vil si isomorft med .
Polynomligninger
[rediger | rediger kilde]En ligning der et polynom er satt lik null kalles en polynomligning. Andregradsligningen er et velkjent eksempel.
Fundamentalteoremet i algebra
[rediger | rediger kilde]Ifølge algebraens fundamentalteorem har et komplekst -te-grads polynomligning av én variabel eksakt røtter, når multiplisiteten til rota er tatt i betraktning. Dersom røttene er kjente, så kan polynomet skrives på forma
Overføring av polynomet til ei slik form kalles faktorisering av polynomet. Røttene trenger ikke være reelle, selv om koeffisientene i polynomet er relle. Kvadratsetningene er eksempel på faktorisering av andregradspolynom.
Løsning av polynomligninger
[rediger | rediger kilde]Løsning av andregradsligninger har vært studert siden babylonertiden, 1600 år f.Kr. Den generelle forma for løsningen av andregradsligningen ved den såkalte ABC-formelen er velkjent. Også løsning av tredjegradsligninger og fjerdegradsligninger kan uttrykkes på sluttet form ved hjelp av aritmetiske operasjoner og rotutdraginger. Cardanos metode gir løsningen av den generelle tredjegradsligningen, mens Ferraris metode kan brukes for fjerdegradsligninger.
I 1824 viste Niels Henrik Abel at dette ikke er mulig for løsningen av den generelle polynomligningen av grad større eller lik fem, og dette resultatet er kjent som Abel-Ruffini-teoremet. Merk at fundamentalteoremet viser at også femtegradsligninger alltid har løsninger, – en kan bare ikke alltid uttrykke disse på sluttet form.
I Galois-teori studerer en relasjoner mellom røttene i polynomligninger.
Funksjonstilnærming med polynom
[rediger | rediger kilde]Weierstrass’ approksimasjonsteorem, navngitt etter Karl Weierstrass, sier at en vilkårlig kontinuerlig funksjon definert på et intervall kan tilnærmes uniformt så nøyaktig en bare vil ved hjelp av polynomfunksjoner. Resultatet kalles også Stone-Weierstrass’ teorem.
Formelt kan en uttrykke dette, som følger: Gitt en kontinuerlig funksjon definert på intervallet og et vilkårlig positivt tall . Da eksisterer det et polynom slik at
Tilnærming ved Taylorutvikling
[rediger | rediger kilde]En funksjon som er uendelig mange ganger deriverbar blir ofte tilnærmet ved hjelp av et polynom definert ved taylorrekka til funksjonen. I et område nær argumentet er tilnærmingen gitt ved
Jo høyere orden i polynomet en bruker, jo bedre er tilnærmingen. I det følgende eksempelet er feilen i tilnærmingen mindre en 0,000003 i intervallet [-1,1]:
Ortogonale polynom
[rediger | rediger kilde]I vektorrom av polynom kan en definere mange alternative indreprodukt, for polynom av én variabel ofte gitt på den følgede forma
To polynom er ortogonale dersom indreproduktet er lik null. Ulike definisjoner av vektfunksjonen ) vil føre til ulike definisjoner av ortogonale polynom, og det eksisterer en lang rekke typer som alle har mange anvendelser der de brukes til å tilnærme mer generelle funksjoner og til interpoloasjon. Ulike klasser av ortogonale polynom er typisk oppkalt etter en matematiker som har bidratt til utvikling av teorien for disse:
- Chebyshev-polynom, oppkalt etter Pafnutij Tsjebysjov
- Hermitske polynom, oppkalt etter Charles Hermite
- Jacobi-polynom, oppkalt etter Carl Gustav Jacob Jacobi
- Laguerre-polynom, oppkalt etter Edmond Laguerre
- Legendre-polynom, oppkalt etter Adrien-Marie Legendre
Splinefunksjoner
[rediger | rediger kilde]Splinefunksjoner er konstruert ved å sette sammen polynom definert på delintervaller, og disse funksjonene er svært anvendelige til funksjonstilnærminger.
Generaliseringer
[rediger | rediger kilde]Polynom kan genraliseres ved å erstatte et argument med en mer kompliserte funksjon eller en annen datatype.
Trigonometriske polynom
[rediger | rediger kilde]En trigonometrisk polynom er et uttrykk på forma
Matrisepolynom
[rediger | rediger kilde]Et matrisepolynom er et uttrykk på forma
der er ei kvadratisk matrise, slik at matrisemultiplikasjon er definert.
Eksterne lenker
[rediger | rediger kilde]Litteratur
[rediger | rediger kilde]- Hans-Frederik Aas (1974). Forelesningsreferater i matematisk analyse, del I. Bergen: Matematisk institutt, Universitetet i Bergen.
- Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
- Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9.




























![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle \max _{x\in [a,b]}|f(x)-p(x)|<\varepsilon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdd9366950cbca4efe86cb7d011e5b57de7c7933)





![{\displaystyle a_{0}+\sum _{i=1}^{n}\left[a_{i}\sin(ix)+b_{i}\cos(ix)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/927cf9584a43e4e6774074cb6544d66feb3db6fe)

