Bessel-funksjon
En Bessel-funksjon er i matematikk løsninger av Bessel-ligningen
der α er et vilkårlig, komplekst tall.
Bessel-funksjonene ble først utledet av matematikeren Daniel Bernoulli og senere generalisert av Friedrich Bessel.
Definisjon[rediger | rediger kilde]

Bessel-funksjoner av første og andre type er to lineært uavhengige løsninger av Bessel-ligningen.
Bessel-funksjoner av første type er definert ved:
- .
der Γ(z) er gammafunksjonen. Dersom α er et heltall er Jα(x) = (-1)nJ−α(x).
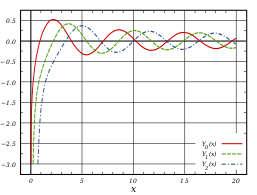
Bessel-funksjoner av andre type er definert ved:
- .
Dersom α er et heltall er Yα(x) = (-1)nY−α(x).



