Lineær funksjon

Se også: Lineær transformasjon og lineær funksjonal

Eksempel på rettlinjede funksjoner

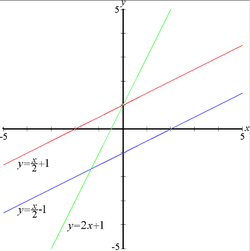
En funksjon av én variabel f(x) sies å være lineær dersom den grafisk framstiller en rett linje. Det generelle uttrykket for slike funksjoner er f(x) = ax + b, og eksempler er vist i figuren til høyre. Koeffisienten a kalles stigningstallet.

I høyere matematikk regnes ikke dette ikke en lineær transformasjon, men derimot et eksempel på en affin transformasjon.

Nyttige formler

Stigningstallet for en rettlinjet funksjon kan bestemmes fra to punkt på kurva

$a={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$

Praktiske eksempler

Det koster 250 kroner for medlemskap i en CD-klubb og 79,50 per cd. Funksjon for hvor mye det koster for x cd-er: f(x) = 79,50x + 250

En tv koster 5000 kroner. Samtidig må man betale 2000 kroner i året i avgifter. Funksjonen for hvor mye det koster å se på denne tv-en i x år: g(x) = 2000x + 5000

Eksterne lenker

• Linear Functions on Id Mind – Engelsk