Pytagoras’ læresetning: Forskjell mellom sideversjoner
Totalrenovering, se Diskusjon |
|||
| Linje 1: | Linje 1: | ||
[[Fil:Pythagorean.svg|thumb|En rettvinklet trekant med de to katetene <math>a</math> og <math>b</math> og hypotenusen <math>c</math>.]] |
[[Fil:Pythagorean.svg|thumb|En rettvinklet trekant med de to katetene <math>a</math> og <math>b</math> og hypotenusen <math>c</math>.]] |
||
'''Pytagoras' læresetning''' eller '''den pytagoreiske læresetning''' er i [[euklidsk geometri]] et fundamentalt [[teorem]] om sammenhengen mellom sidelengdene i en [[rettvinklet trekant]]: |
|||
'''Pythagoras' læresetning''' er en av de mest grunnleggende [[doktrine|læresetning]]er innen [[euklidsk geometri]] og kan uttrykkes som: |
|||
:''«I en rettvinklet trekant er summen av kvadratene på katetene lik kvadratet på hypotenusen.»'' |
|||
<blockquote> |
|||
''«I en [[rettvinklet trekant]] er summen av kvadratene på [[katet]]ene lik kvadratet på [[hypotenus]]en.»'' |
|||
</blockquote> |
|||
De to |
De to [[katet]]ene er de korteste sidene i trekanten, og [[hypotenus]]en er den lengste. Den rette vinkelen er motstående til hypotenusen. Kaller man lengdene av katetene henholdsvis <math>a</math> og <math>b</math> samt lengden av hypotenusen for <math>c</math>, så kan læresetningen uttrykkes som en [[ligning (matematikk)|ligning]], ofte kalt '''Pytagoras ligning''':<ref name=JS>{{kilde bok |tittel=Roots to research: A vertical development of mathematical problems |forfatter=Judith D. Sally, Paul Sally |språk=en |side=63ff |url=https://books.google.com/books?id=nHxBw-WlECUC&pg=PA63 |isbn=978-0-8218-4403-8 |år=2007 |forlag=American Mathematical Society Bookstore}}</ref> |
||
:<math>a^2 + b^2 = c^2 |
:<math>a^2 + b^2 = c^2</math>. |
||
Heltall som oppfyller Pytagoras' læresetning kalles pytagoreiske tripler. Et velkjent trippel er (3,4,5). Dersom sidelengdene i en trekant danner et pytagoreiske trippel, så er trekanten rettvinklet. |
|||
Pythagoras' læresetning har sitt navn etter den [[Antikkens Hellas|greske]] [[matematiker]]en [[Pythagoras]] som ansees å være den som oppdaget og beviste setningen.<ref name="Heath, Vol I, p. 144">Heath, Vol I, p. 144.</ref> Blant matematikere trekkes dette i tvil. Lenge før Pythagoras' tid synes sammenhengen i Pythagoras' læresetning å være kjent både i [[Babylon]], [[Kina]] og [[India]], men uten at man har kunnet påvise at de [[Matematisk bevis|beviste]] [[teorem]]et. |
|||
Det eksisterer mange generaliseringer av Pytagoras' teorem. En generalisering til en vilkårlig [[trekant]] kalles ''den utvidede pytagoreiske læresetning'' eller [[cosinussetningen]]. |
|||
Det historiske opphavet til teoremet er bare mangelfullt kjent og har vært gjenstand for mye diskusjon. Navnet har teoremet fått fordi mange tradisjonelt har knyttet læresetningen til den greske matematikeren [[Pythagoras|Pytagoras]], som levde omkring 500 f.Kr. Det eksisterer imidlertid ikke gode indikasjoner eller bevis for at han eller noen av hans følgesvenner skal ha vært opphavsmann til teoremet. Pytagoreiske tripler og andre former for teoremet har vært kjent i [[Babylonsk matematikk|babylonsk]], [[Oldtidens egyptiske matematikk|egyptisk]], [[kinesisk matematikk|kinesisk]] og [[indisk matematikk]] lenge før pytagoreerne. Kanskje har læresetningen blitt oppdaget flere steder og til flere tider uavhengig av hverandre. Det eldste deduktive bevis vi kjenner, er fra [[Euklids Elementer|Euklids ''Elementer'']], skrevet omkring 300 f.Kr. I dag eksisterer det en lang rekke alternative bevis for teoremet. |
|||
== Bevis == |
== Bevis == |
||
[[Fil:Illustration to Euclid's proof of the Pythagorean |
[[Fil:Illustration to Euclid's proof of the Pythagorean theorem2.svg|thumb|Geometri for Euklids bevis.]] |
||
[[Fil:Euclidis elementorum libri priores sex Fleuron T145401-9.png|thumb|Illustrasjon til Euklids bevis fra 1756. Lignende figurer er blitt beskrevet som en «vindmølle», en «brudestol» og en «påfugl-hale».]] |
|||
[[Fil:Illustration to Euclid's proof of the Pythagorean theorem2.svg|thumb|Illustrasjon med hjelpelinjer.]] |
|||
Pytagoras' læresetning antas å være et av de teoremene i matematikk som er bevist på flest alternative måter. Boken ''Pythagorean Proposition'' av Elisha Scott Loomis inneholder hele 370 bevis.<ref name=ESL1>[[#ESL| E.S. Loomis: ''The Pythagorean proposition'']] s.1 </ref> I boken er 109 bevis karakterisert som algebraiske og 255 som geometriske. De resterende seks er basert på vektorregning eller dynamiske argument. Et ''geometrisk'' bevis bygger i følge Loomis på sammenligning av [[areal]]et til de tre kvadratene konstruert fra sidelengdene, mens et ''aritmetisk'' er basert på lineære relasjoner mellom sidelengder eller areal, for eksempel ved bruk av [[Trekant#Formlike trekanter|formlike]] trekanter. Denne inndelingen er kanskje ikke entydig, og mange bevis har innslag av både geometri og algebra. |
|||
[[Fil:PythagoreEuclide1.gif|thumb|Animasjon av Euklids bevis.]] |
|||
Pythagoras' læresetning antas å være et av de teoremene innen matematikken som er bevist på flest måter. Boken ''Pythagorean Proposition'' av Elisha Scott Loomis inneholder hele 367 bevis. |
|||
=== Euklids bevis === |
=== Euklids bevis === |
||
I Euklids ''Elementer'', teorem 47 i bok I, finner man det eldste kjente beviset for Pytagoras' teorem.<ref name=BO119>[[#BOYER|C.B.Boyer: ''A history of mathematics'']] s.119 </ref><ref name=P47>{{kilde www| url=http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0086%3Abook%3D1%3Atype%3DProp%3Anumber%3D47 |tittel=Euclid ''Elements''. Proposition 47 |språk=en |utgiver=Persus Digital Library |besøksdato=2021-03-12}}</ref> Det er vanlig å referere til Euklids bøker med romertall for bindet og et vanlig tall for den gjeldende satsen, slik at Pytagoras' teorem er I.47. |
|||
I [[Evklid]]s ''[[Euklids Elementer|Elementer]]'', teorem 47 i bok 1 finner man det mest klassiske beviset for Pythagoras' teorem. |
|||
Beviset for I.47 er basert på en sammenligning av areal. |
|||
La <math>A</math>, <math>B</math> og <math>C</math> være hjørnene i en rettvinklet trekant med den rette vinkel ved <math>A</math> som vist på figuren. |
La <math>A</math>, <math>B</math> og <math>C</math> være hjørnene i en rettvinklet trekant, med den rette vinkel ved <math>A</math> som vist på figuren. Til hver side i trekanten er det tegnet et [[kvadrat]]. En [[normal (geometri)|normal]] fra hjørnet <math>A</math> til hypotenusen <math>BC</math> deler kvadratet på hypotenusen i to [[rektangel|rektangler]], på figure vist i blått og rosa. Euklid beviste setningen ved å vise at arealet til hver av de to minste kvadratene er lik arealet av ett av rektanglene, vist med fargene i figuren. Arealsummen av de to minste kvadratene er dermed lik arealet til det største kvadratet. |
||
Beviset bygger på flere [[lemma (matematikk)|hjelpesetninger]], som Euklid viser tidligere i bok I. Disse vil bli brukt videre, uten bevis her. |
|||
Før vi går videre, trengs tre kjente lemma: |
|||
# Hvis to trekanter er slik at to sider i den ene er lik tilsvarende to sider i den andre og den mellomliggende vinkel er lik i begge, så er trekantene [[Kongruens (geometri)|kongruente]]. |
# Hvis to trekanter er slik at to sider i den ene er lik tilsvarende to sider i den andre, og den mellomliggende vinkel er lik i begge, så er trekantene [[Kongruens (geometri)|kongruente]]. |
||
# Arealet av en gitt trekant er lik halvparten av |
# Arealet av en gitt trekant er lik halvparten av arealet i et vilkårlig [[parallellogram]] med samme grunnlinje og høyde. |
||
# Arealet av |
# Arealet av et rektangel er lik produktet av to tilstøtende sider. |
||
# Arealet av et |
# Arealet av et kvadrat er lik produktet av to sider. |
||
For å lette tankegangen i dette beviset kan en tenke seg at kvadratet på det øvre, venstre kvadratet omformes til et parallellogram med samme størrelse. Dette dreies og omformes til henholdsvis det venstre og det høyre rektangelet i det nedre kvadratet.<ref>Mike May S.J., [http://www.slu.edu/classes/maymk/GeoGebra/Pythagoras.html Pythagorean theorem by shear mapping] {{Wayback|url=http://www.slu.edu/classes/maymk/GeoGebra/Pythagoras.html |date=20161014165156 }}, Saint Louis University website Java applet</ref> |
|||
Beviset er som følger: |
Beviset er som følger: |
||
#La <math>ACB</math> være en rettvinklet trekant med den rette |
#La <math>ACB</math> være en rettvinklet trekant, med den rette vinkelen gitt ved <math>\angle BAC</math>. |
||
#På hver av sidene <math>BC</math>, <math>AB</math> |
#På hver av sidene <math>BC</math>, <math>AB</math> og <math>CA</math> tegnes kvadrater, henholdsvis <math>CBDE</math>, <math>BAGF</math> og <math>ACIH</math>. |
||
#Fra <math>A</math> trekkes en linje parallell med <math>BD</math> og <math>CE</math>. Den |
#Fra <math>A</math> trekkes en linje parallell med <math>BD</math> og <math>CE</math>. Den krysser <math>BC</math> og <math>DE</math> i rett vinkel ved henholdsvis <math>K</math> og <math>L</math>. |
||
#Forbind <math>CF</math> og <math>AD</math>. Derved dannes trekantene <math>BCF</math> og <math> |
#Forbind <math>CF</math> og <math>AD</math>. Derved dannes trekantene <math>BCF</math> og <math>ADB</math>. |
||
#Vinklene <math>CAB</math> og <math>BAG</math> er begge rette. |
#Vinklene <math>\angle CAB</math> og <math>\angle BAG</math> er begge rette. Punktene <math>C</math>, <math>A</math> og <math>G</math> ligger derfor på samme linje. Tilsvarende ligger <math>B</math>, <math>A</math> og <math>H</math> på en rett linje. |
||
#Vinklene <math>CBD</math> og <math>FBA</math> er begge rette. Dermed er |
#Vinklene <math>\angle CBD</math> og <math>\angle FBA</math> er begge rette. Dermed er <math>\angle ABD</math> lik <math>\angle FBC</math>, siden begge er summen av en rett vinkel og den felles <math>\angle ABC</math>. |
||
#Siden <math>AB</math> og <math>BD</math> er tilsvarende like med <math>FB</math> og <math>BC</math>, må trekanten <math>ABD</math> være kongruent med trekanten <math>FBC</math>. |
#Siden <math>AB</math> og <math>BD</math> er tilsvarende like med <math>FB</math> og <math>BC</math>, må trekanten <math>ABD</math> være kongruent med trekanten <math>FBC</math>. |
||
# |
#Ved bruk av hjelpesetning nr.2 må rektangelet <math>BDLK</math> være dobbelt så stort som trekanten <math>ABD</math>. |
||
# |
#Ved bruk av hjelpesetning nr.2 må rektangelet <math>BAGF</math> være dobbelt så stort som trekanten <math>FBC</math>. |
||
#Dermed må rektangelet <math>BDLK</math> ha samme areal som kvadratet <math>BAGF |
#Dermed må rektangelet <math>BDLK</math> ha samme areal som kvadratet <math>BAGF</math>, det vil si at <math>AB^2 = BD \times BK</math>. |
||
#Tilsvarende kan det vises at rektangelet <math>CKLE</math> må ha samme areal som kvadratet <math>ACIH |
#Tilsvarende kan det vises at rektangelet <math>CKLE</math> må ha samme areal som kvadratet <math>ACIH</math>, det vil si at <math>AC^2 = KL \times KC</math>. |
||
#Ved å addere disse to resultatene: <math>AB^2 + AC^2 = BD \times BK + KL \times KC</math>. |
#Ved å addere disse to resultatene: <math>AB^2 + AC^2 = BD \times BK + KL \times KC</math>. |
||
#Siden <math>BD = KL, BD \times BK + KL \times KC = BD(BK \times KC) = BD \times BC</math>. |
#Siden <math>BD = KL</math>, så er <math> BD \times BK + KL \times KC = BD(BK \times KC) = BD \times BC</math>. |
||
#Dermed er <math>AB^2 + AC^2 = BC^2</math> siden <math>CBDE</math> er et kvadrat. |
#Dermed er <math>AB^2 + AC^2 = BC^2</math>, siden <math>CBDE</math> er et kvadrat. |
||
Dette beviset er gitt i Euklids ''Elementer'' som teorem 1'''.'''47.<ref> |
|||
[http://www.perseus.tufts.edu/cgi-bin/ptext?doc=Perseus:text:1999.01.0085:book=1:proposition=47 Elements 1.47] by Euclid, retrieved 19 December 2006 |
|||
</ref> |
|||
Dette beviset har vært i bruk i norsk [[realskole]]. Det er unødvendig komplisert for å bevise Pythagoras' læresetning, men kan være en egnet øvelse i matematisk tenkning. |
|||
Beviset har tidligere vært pensum i norsk [[realskole]].{{tr}} Det finnes enklere bevis, men gjennomgang av fremgangsmåten kan være en egnet øvelse i matematisk tenkning. |
|||
=== Bevis ved bruk av likedannede trekanter === |
|||
[[Fil:Proof-Pythagorean-Theorem.svg|thumb|Bevis ved bruk av likedannede trekanter.|left]] |
|||
Dette beviset er, som de fleste, basert på proporsjonene av sidene i to likedannede trekanter. |
|||
Figuren til Euklids bevis, med hjelpelinjer til alle fire kvadrater, er berømt. Den er blitt beskrevet som en «vindmølle», en «brudestol» og en «påfugl-hale».<ref name=BO119/> |
|||
La <math>ABC</math> representere en rettvinklet trekant med den rette vinkelen ved <math>C</math> slik figuren viser. Vi trekker høyden fra hjørnet <math>C</math> og kaller fotpunktet på siden <math>AB</math> for <math>H</math>. Det nye trianglet <math>ACH</math> er likedannet med triangelet <math>ABC</math> da de begge er rettvinklede pr. definisjon av høyden og de deler vinkelen ved <math>A</math>. Derved er også den siste vinkelen lik og trekantene likedannede. Tilsvarende er triangelet <math>CBH</math> likedannet med <math>ABC</math>. Dette kan uttrykkes ved følgende forhold: |
|||
Også navnet [[pons asinorum]] er blitt brukt om figuren.<ref name=ESL120>[[#ESL| E.S. Loomis: ''The Pythagorean proposition'']] s.120 </ref> Dette latinske utrrykket betyr |
|||
«eselbroen» eller «idiotbroen», og uttrykket knyttes vanligvis til en annen Euklid-figur, brukt i forbindelse med ''Elementer'' I.5.<ref>{{kilde bok | forfatter= David Eugene Smith |tittel=History of mathematics |bind=II |forlag=Ginn and Company |år= 1925 |språk=en |side=284 |url=https://archive.org/details/historyofmathema031897mbp/page/n299/mode/2up?q=pons }}</ref> |
|||
=== Bevis ved bruk av formlike trekanter === |
|||
:<math> \frac{a}{c}=\frac{HB}{a} \mbox{ og } \frac{b}{c}=\frac{AH}{b} \ .</math> |
|||
[[Fil:Proof-Pythagorean-Theorem.svg|thumb|right|Bevis ved bruk av likedannede trekanter.]] |
|||
Disse kan skrives som |
|||
Mange av bevisene for Pytagoras' setning er basert på forhold mellom sidelengder i to formlike trekanter. Elisha Scott Loomis omtaler dette som det korteste av alle Pytagoras-bevisene og kaller det også for «Legendre-beviset».<ref name=ESL24>[[#ESL| E.S. Loomis: ''The Pythagorean proposition'']] s.24 </ref> |
|||
:<math>a^2=c\times HB \mbox{ og }b^2=c\times AH \ .</math> |
|||
En lærebok i geometri fra 1858, basert på arbeid av [[Adrien-Marie Legendre]], gjengir beviset. [[Thomas Heath]] foreslår dette som ett alternativ for et bevis som kan ha vært brukt av pytagoreerne.<ref name=TH144>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.144-149 </ref> |
|||
Ved å summere disse to likheter: |
|||
:<math>a^2+b^2=c\times HB+c\times AH=c\times(HB+AH)=c^2 \ .</math> |
|||
La <math>ABC</math> være en rettvinklet trekant. Den rette vinkelen er ved <math>C</math>, slik figuren viser. Høyden fra hjørnet <math>C</math> treffer siden <math>AB</math> i fotpunktet <math>H</math>. |
|||
Med andre ord: Pythagoras' teorem: |
|||
Trekanten <math>ACH</math> er formlik med trekanten <math>ABC</math>, da begge er rettvinklede og vinkelen ved <math>A</math> er felles. Tilsvarende er trekanten <math>CBH</math> formlik med <math>ABC</math>. |
|||
:<math>a^2+b^2=c^2\ .</math> |
|||
Tilsammen resulterer dette i følgende forhold mellom sidelengder: |
|||
:<math> \frac{a}{c}=\frac{HB}{a} \qquad \text{og} \qquad \frac{b}{c} = \frac{AH}{b} \ .</math> |
|||
Dette kan skrives som |
|||
:<math>a^2=c\times HB \qquad \text{og} \qquad b^2= c \times AH \ .</math> |
|||
Summasjon av de to uttrykkene gir |
|||
:<math> |
|||
a^2+b^2=c\times HB+c\times AH=c\times(HB+AH)=c^2 . |
|||
</math> |
|||
=== Garfields bevis === |
=== Garfields bevis === |
||
[[Fil:Aa garfield pythag.svg|thumb|right|Garfields bevis.]] |
[[Fil:Aa garfield pythag.svg|thumb|right|Geometri brukt i Garfields bevis.]] |
||
[[James Garfield]] er opphavsmann for det følgende beviset.<ref>{{kilde www |utgiver= Angie Head, University of Georgia | url=http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/HeadAngela/essay1/Pythagorean.html |tittel=Pythagorean theorem |språk=en |besøksdato=2021-03-12}}</ref><ref name=MAA>{{kilde www| url=https://www.maa.org/press/periodicals/convergence/mathematical-treasure-james-a-garfields-proof-of-the-pythagorean-theorem | tittel=Mathematical Treasure: James A. Garfield's Proof of the Pythagorean Theorem | språk=en |utgiver=Mathematical Association of America | besøksdato=2021-03-12}}</ref> |
|||
[[James A. Garfield]] (senere president i USA) er tilkjent æren for dette moderne, algebraiske bevis:<ref> |
|||
Han var jurist og medlem av den amerikanske [[Kongressen (USA)|Kongressen]], og han oppdaget beviset i 1876 som følge av en matematisk diskusjon med andre kongressmedlemmer. Garfield ble president i USA i 1881, men han ble skutt og drept etter bare fire måneder i embedet. |
|||
Head, Angie. [http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/HeadAngela/essay1/Pythagorean.html «Pythagorean Theorem»] |
|||
</ref> |
|||
Arealet av et generelt [[trapes]] med høyde <math>h</math> og lengder av de to parallelle sidene <math>s_1</math> og <math>s_2</math> er gitt ved |
|||
:<math>A=\frac{h}{2}(s_1 + s_2).</math> |
|||
Arealet av et [[trapes]] er gitt ved. |
|||
:<math>A=\frac{h}{2}(s_1 + s_2)</math> |
|||
hvor <math>h</math> er høyden (avstanden mellom de parallelle sidene) og <math>s_1</math> og <math>s_2</math> er lengden av de parallelle sidene. |
|||
Da er arealet av trapeset vist i figuren: |
Da er arealet av trapeset vist i figuren: |
||
:<math>A=\frac{(a+b)}{2}(a + b) = \frac{(a+b)^2}{2} |
:<math>A=\frac{(a+b)}{2}(a + b) = \frac{(a+b)^2}{2} .</math> |
||
Trekant 1 og 2 er identiske, med areal |
|||
Idet triangel <math>1</math> og triangel <math>2</math> begge har et areal: <math> \frac{ab}{2}</math> |
|||
:<math>A_1 = A_2 = \frac{ab}{2}.</math>. |
|||
Trekant 3 er rettvinklelt, og arealet er lik halvparten av kvadratet på hypotenusen: |
|||
Da er arealet av trapeset: |
|||
: <math>A = \frac{ab}{2} + \frac{ab}{2} + \frac{c^2}{2} = ab + \frac{c^2}{2} \ .</math> |
|||
:<math>A_3 = \frac{c^2}{2}. </math> |
|||
De to arealene må være like. Derved er |
|||
Et alternativt uttrykk for arealet til trapeset finner en ved å summere arealene til de tre trekantene: |
|||
<math>\frac{(a+b)^2}{2} = ab + \frac{c^2}{2} </math> |
|||
<math>\frac{ |
: <math>A = A_1 + A_2 + A_3 = \frac{ab}{2} + \frac{ab}{2} + \frac{c^2}{2} = ab + \frac{c^2}{2} \ .</math> |
||
En sammenstillingen av de to uttrykkene for trapesarealet gir |
|||
<math> a^2 + 2ab + b^2 \mathbf{=} 2ab + c^2 \ .</math> |
|||
:<math> |
|||
Dermed er kvadratet på hypotenusen lik summen av kvadratene på katetene: |
|||
\begin{alignat}{2} |
|||
\frac{(a+b)^2}{2} \ &= \ ab + \frac{c^2}{2} \\[5pt] |
|||
a^2 + 2ab + b^2 \ &= \ 2ab + c^2 \\[5pt] |
|||
a^2 + b^2 \ &= \ c^2 . |
|||
\end{alignat} |
|||
</math> |
|||
=== Bevis ved reorganisering === |
=== Bevis ved reorganisering === |
||
[[Fil: |
[[Fil:Pythagoras-proof-anim.svg|thumb|Bevis av Pytagoras' teorem ved reorganisering. Klikk på bildet for animasjon.|left]] |
||
Det eksisterer flere bevis basert på å reorganisere areal. Et eksempel er vist i figuren til venstre. De to store kvadratene i figuren er like store, begge med sidelengde <math>a + b</math>. |
|||
De to kvadratene skiller seg kun ved den innvendige plasseringen av de fire trekantene. Arealet av de hvite områdene i de to store kvadratene må derfor være like, og dette gir Pytagoras' setning. |
|||
Thomas Heath omtaler dette beviset og et forslag fra de to matematikerne [[Carl Anton Bretschneider]] og [[Hermann Hankel]] om at dette kan ha vært kjent av pytagoreerne.<ref name=TH144/> |
|||
Et bevis med bruk av rearrangering er vist i animasjonen. I illustrasjonen er arealet av det store kvadratet <math>(a + b)^2</math>. I begge er arealet av fire identiske triangler tatt bort. Det resterende areal: <math>a^2 + b^2</math> og <math>c^2</math> er like. [[Q.E.D.]] |
|||
Heath vil ikke avvise en slik teori, men mener selv at det er mer sannsynlig at pytagoreerne kjente beviset basert på formlike trekanter. |
|||
{{-}} |
|||
=== Algebraisk bevis === |
=== Algebraisk bevis === |
||
[[Fil:Pythagproof.svg|thumb|Algebraisk bevis med fire identiske |
[[Fil:Pythagproof.svg|thumb|Algebraisk bevis med fire identiske trekanter i et større kvadrat.]] |
||
Et algebraisk bevis kan gjennomføres ved å betrakte fire identiske |
Et algebraisk bevis kan gjennomføres ved å betrakte fire identiske trekanter plassert i hjørnene til et større kvadrat.<ref name=CUT4>{{kilde www |url=http://www.cut-the-knot.org/pythagoras/index.shtml#4 |tittel=Pythagorean theorem. Proof 4 |språk=en |utgiver=Cut the Knot |besøksdato=2021-03-13}}</ref> |
||
Beviset er gjengitt av den indiske matematikeren [[Bhaskara]], som levde på 1200-tallet. |
|||
Sidelengdene i trekantene er <math>A</math>, <math>B</math> og <math>C</math>, og det store kvadratet har sidelengde <math>A + B</math>. |
|||
:<math>\frac{1}{2} AB \ .</math> |
|||
Arealet <math>S_T</math> av hver av de fire trekantene er gitt ved: |
|||
Siden motstående vinkel til <math>A</math>-siden og <math>B</math>-siden i hver av disse trianglene er komplementære vinkler, må det blå arealet være et kvadrat med areal lik <math>C^2</math>. |
|||
Det samlede areal er gitt ved: |
|||
:<math>4\left(\frac{1}{2}AB\right)+C^2 \ .</math> |
|||
Idet lengden av sidene i det store kvadratet kan også uttrykkes som <math>A + B</math> og areal <math>(A + B)^2</math>, som kan skrives som <math>A^2 + 2AB + B^2</math>. |
|||
:<math>S_T = \frac{1}{2} AB \ .</math> |
|||
Da er: |
|||
I hver trekant er motstående vinkel til <math>A</math>-siden og <math>B</math>-siden [[komplementvinkler]]. Også det blå området er derfor et kvadrat, med areal lik <math>C^2</math>. |
|||
: <math>A^2+2AB+B^2=4\left(\frac{1}{2}AB\right)+C^2\,\!</math> |
|||
Arealet <math>S</math> til det store kvadratet med sidelengde <math>(A + B)</math> er gitt ved |
|||
: <math>A^2+2AB+B^2=2AB+C^2\,\!</math> (Multiplikasjon med 4) |
|||
: <math>A^2+B^2=C^2\,\!</math> (Subtraksjon av 2''AB''). |
|||
:<math>S = (A + B)^2</math> |
|||
== Det inverse av teoremet == |
|||
Det inverse teoremet gjelder også: |
|||
<blockquote> |
|||
For tre vilkårlige positive tall ''a'', ''b'' og ''c'' der {{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}} finnes det et triangel med sider ''a'', ''b'' og ''c''. Ethvert slikt triangel er et rett triangel med den rette vinkel mellom sidene med lengde ''a'' og ''b''. |
|||
</blockquote> |
|||
Alternativt kan dette uttrykkes som arealsummen for de fire trekantene og det blå kvadratet: |
|||
Dette utsagnet finnes også i Euklids ''Elementer''. Det kan bevises ved bruk av [[cosinussetningen]], eller som følger: |
|||
:<math>S = 4S_T + C^2 = 4\left(\frac{1}{2}AB \right) + C^2 \ .</math> |
|||
La ''ABC'' være et triangel med sidelengder ''a'', ''b'' og ''c'' slik at{{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}}. Vi konstruerer et nytt, rett triangel med den rette vinkel mellom sidene med lengde ''a'' og ''b''. At hypotenusen i det nye trianglet har lengde ''c'' følger av Pythagoras' læresetning. Siden begge triangler har sider med lengde ''a'', ''b'' og ''c'' er de [[Kongruens (geometri)|kongruente]] og følgelig må de ha de samme vinkler i hjørnene. Derav følger at vinkelen mellom sidene av lengde ''a'' and ''b'' i vårt første triangel, er en rett vinkel. |
|||
En sammenstilling av de to uttrykkene for <math>S</math> gir Pytagoras' teorem. |
|||
En konsekvens av den inverse pytagoreiske læresetning gir oss en enkel metode for å bestemme om et trianglet er rett, spisst eller butt. Gitt at ''c'' er den lengste av sidene: |
|||
* Hvis {{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}}, så er triangelet rett. |
|||
* Hvis {{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> > ''c''<sup>2</sup>}}, så er trianglet spisst (alle vinkler er spisse). |
|||
* Hvis {{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> < ''c''<sup>2</sup>}}, så er triangelet butt (én vinkel er butt). |
|||
== Det omvendte teoremet == |
|||
Dette kan også uttrykkes slik: |
|||
Euklid viste i teorem I.48 at også det omvendte Pytagoras' teorem er gyldig, der en bytter forutsetning og konklusjon:<ref name=P48>{{kilde www| url=http://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.01.0086%3Abook%3D1%3Atype%3DProp%3Anumber%3D48 |tittel=Euclid ''Elements''. Proposition 48 |språk=en |utgiver=Persus Digital Library |besøksdato=2021-03-12}}</ref> |
|||
I et triangel med tre spisse vinkler gjelder: ''α'' + ''β'' > ''γ''. Da er ''a''<sup>2</sup> + ''b''<sup>2</sup> > ''c''<sup>2</sup>. |
|||
:''«For tre vilkårlige, positive tall a, b og c der {{Nowrap|a<sup>2</sup> + b<sup>2</sup> {{=}} c<sup>2</sup>}}, finnes det en rettvinklet trekant med sider a, b og c. Den rette vinkelen er mellom sidene med lengde a og b.»'' |
|||
I et triangel med en butt vinkel gjelder: ''α'' + ''β'' < ''γ''. Da er. ''a''<sup>2</sup> + ''b''<sup>2</sup> < ''c''<sup>2</sup>. |
|||
Teoremet kan bevises som følger: |
|||
[[Edsger Dijkstra]] har fremsatt en sats om spisse, rette, and butte triangler på denne måten ved bruk av fortegnsfunkjonen: |
|||
::[[Signum (Matematikk)|sgn]](''α'' + ''β'' − ''γ'') = sgn(''a''<sup>2</sup> + ''b''<sup>2</sup> − ''c''<sup>2</sup>) |
|||
La <math>ABC</math> være en trekant med sidelengder <math>a</math>, <math>b</math> og <math>c</math>. Anta også at <math>a^2 + b^2 = c^2</math>. Konstruerer en ny rettvinklet trekant <math>KLM</math>, med den rette vinkelen mellom sider med lengde <math>a</math> og <math>b</math>. Fra Pytagoras' setning følger det at hypotenusen i trekant <math>KLM</math> har lengde <math>c</math>. Trekantene <math>ABC</math> og <math>KLM</math> har tre like sider og er derfor kongruente. Følgelig har de også like vinkler. I trekant <math>ABC</math> må derfor vinkelen mellom sidelengdene <math>a</math> and <math>b</math> være en rett vinkel. |
|||
hvor ''α'' er vinkelen med motstående side ''a'', ''β'' er vinkelen med motstående side ''b'' og ''γ'' er vinkelen med motstående side ''c''.<ref> |
|||
{{Cite web |
|||
|url=http://www.cs.utexas.edu/users/EWD/ewd09xx/EWD975.PDF |
|||
|title=Dijkstra's generalization |
|||
|format=PDF}} |
|||
</ref> |
|||
== Pytagoreiske tripler == |
|||
== Betydning og bruk av læresetningen == |
|||
Et pytagoreisk trippel består av tre positive [[heltall]] <math>a</math>, <math>b</math>, og <math>c</math>, slik at <math>a^2 + b^2 = c^2</math>.<ref name=HW245>{{Kilde bok | forfatter= G.H. Hardy, E.W. Wright| utgivelsesår=2008| tittel=An introduction to the theory of numbers| forlag=Oxford University Press| utgivelsessted=Oxford| side=245-247| isbn=978-0-19-921985-8}}</ref> |
|||
=== Pytagoreiske tripler === |
|||
En vanlig skrivemåte for et slikt trippel er <math>(a, b, c)</math>. Et pytagoreiske trippel representerer sidelengdene i en rettvinklet trekant, når alle tre lengdene har heltallsverdier. Et velkjent eksempel er (3,4,5). |
|||
Et pytagoreisk trippel består av tre positive heltall ''a'', ''b'', og ''c'' slik at {{Nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}}. Med andre ord representerer et pytagoreiske trippel sidene i en rettvinklet trekant der alle tre sidene har [[heltall]]sverdier. [[Megalittisk monument|Megalittiske monumenter]] fra Nord-Europa viser at slike tripler var kjent allerede før skrivekunsten. Det er vanlig å skrive slike tripler som {{Nowrap|(''a'', ''b'', ''c'')}}. |
|||
Dersom <math>(a, b, c)</math> er et pytagoreisk trippel, så vil også <math>(na, nb, nc)</math> være det, for et vilkårlig heltall <math>n</math>. Dersom de tre tallene <math>a</math>, <math>b</math>, og <math>c</math> ikke har noen felles faktor, så kalles de tre tallene for et ''primitivt'' trippel.<ref name=JS/> Tallene er da [[relativt primisk]]e. Mens (3, 4, 5) er et primitivt trippel, er (6, 8, 10) et trippel med en felles faktor 2. |
|||
Mens (3, 4, 5) omtales som et primitivt trippel, er (6, 8, 10) ikke et primitivt trippel. En ser at en kan dividere alle ledd i (6, 8, 10) med 2 og komme til (3, 4, 5). |
|||
Pytagoreiske tripler kan brukes til å konstruere rette vinkler og til å kontrollere om en gitt vinkel er rett. Et hendig trippel er (60,80,100), et ikke-primitivt trippel som kan dannes ved å multiplisere tallene i (3,4,5) |
|||
Et hendig trippel er (3, 4, 5) multiplisert med 20, slik at man får det ikke-primitive trippel: (60, 80, 100). En kan nå sjekke en vinkel i et innvendig hjørne, for eksempel i et rom, ved å avsette henholdsvis 60 cm langs den ene veggen, 80 cm langs den andre. Om nå [[tommestokk|meterstokken]] passer mellom merkene, er vinkelen rett. Dersom vinkelen ikke er rett, kan en «ta den med» som for eksempel 60, 78, 100. Dette er en litt stump vinkel og tallene er ikke lenger et pytagoreisk trippel. |
|||
med 20. En vinkel i et innvendig hjørne i et rom kan kontrolleres ved å avsette henholdsvis 60 cm langs den ene veggen, 80 cm langs den andre. Om nå en meter-lengde passer mellom merkene, så er vinkelen rett. |
|||
En enkel omforming av ligningen for et pytagoreisk trippel gir |
|||
Et gammelt eksempel på kjennskapet til pytagoreiske tripler er en tauring med 12 knuter. Knutene er ekvidistante. Ved å strekke ut tauet kan en danne en trekant med sidene 3,4,5 og danne en rett vinkel. |
|||
:<math>\left ( \frac{a}{c} \right )^2 + \left ( \frac{b}{c} \right )^2 = 1 </math> |
|||
Å finne pytagoreisk tripler svarer altså til å finne et punkt på en enhetssirkel, der koordinatene er gitt ved to [[rasjonalt tall|rasjonale tall]].<ref name=AH21/> Formler for å konstruere pytagoreiske tripler har vært kjent i svært lang tid. De to følgende formlene skal være funnet av henholdsvis Pytagoras og Platon:<ref name=TH81>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.81 </ref> |
|||
:<math> |
|||
\begin{alignat}{2} |
|||
(a,b,c) &= \left ( \ m^2, \frac{1}{4}(m^2 - 1)^2, \frac{1}{4}(m^2 + 1)^2 \ \right) \qquad m \ \text{oddetall}\\[7pt] |
|||
(a,b,c) &= \left( \ (4m^2, (m^2 - 1)^2, (m^2 + 1)^2 \ \right) |
|||
\end{alignat} |
|||
</math> |
|||
I bok X gir Euklid et enda videre uttrykk for pytagoreiske tripler. Aæren for det generelle uttrykket for alle primitive pytagoreiske tripler er gitt til [[Diofant]], som levde omkring 200 år etter Kristus:<ref name=AH49>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.49 </ref> |
|||
:<math>(a,b,c) = (\ 2uv, u^2 - v^2, u^2 + v^2 \ )</math> |
|||
Her er <math>u</math> og <math>v</math> to vilkårlige, positive heltall som ikke begge er oddetall. Dessuten er <math>u > v</math>, og de to tallene skal ikke ha noen felles faktor. |
|||
=== Primitive pytagoreiske tripler opp til 100 === |
=== Primitive pytagoreiske tripler opp til 100 === |
||
{| |
:{| |
||
|(3, 4, 5), |
|(3, 4, 5), |
||
|- |
|- |
||
| Linje 197: | Linje 213: | ||
|} |
|} |
||
== Konsekvenser og bruk av læresetningen == |
|||
=== Eksistensen av irrasjonale tall === |
|||
En av konsekvensene av Pythagoras' teorem er at en kan konstruere [[Kommensurablitet (matematikk)|inkommensurable]] lengder (ie. forholdet mellom dem er et [[irrasjonalt tall]]). I et triangel med kateter lik 1, er hypotenusen lik kvadratroten av 2. At kvadratroten av to er et irrasjonalt tall, kan vises ved et enkelt algebraisk bevis, se [[Kvadratroten av 2]]. Beviset på at kvadratroten av 2 er et irrasjonalt tall stod i motsetning til oppfatningen om at alt var rasjonalt. Ifølge legenden ble [[Hippasos]] druknet som en konsekvens av at han, som den første, beviste at kvadratroten av to er irrasjonalt.<ref> |
|||
Heath, Vol I, pp. 65, 154; Stillwell, p. 8–9. |
|||
</ref> |
|||
=== Inkommensurable lengder og irrasjonale tall === |
|||
=== Distanse i et kartesisk koordinatsystem === |
|||
En konsekvens av Pytagoras' teorem er at det er mulig å konstruere [[Kommensurablitet (matematikk)|inkommensurable]] lengder, det vil si lengder med et forhold lik et [[irrasjonalt tall]]. Et enkelt eksempel er gitt ved rettvinklet trekant der begge katetene har lengde 1. Pytagoras' setning gir at hypotenusen i en slik trekant har lengde lik kvadratroten av 2. At dette tallet er et irrasjonalt tall, kan vises ved et enkelt algebraisk bevis, se [[Kvadratroten av 2]]. |
|||
Avstandsformelen i et [[Kartesisk koordinatsystem|kartesiske koordinater]] er utviklet ut fra Pythagoras’ teorem: |
|||
For greske matematikere var en irrasjonell størrelse definert som et forhold mellom lengder og ikke som et tall. Det skulle gå lang tid før en forståelse av irrasjonale ''tall'' skulle bli etablert. |
|||
Hvis (''x''<sub>0</sub>, ''y''<sub>0</sub>) og (''x''<sub>1</sub>, ''y''<sub>1</sub>) er |
|||
Eksistensen av inkommensurable lengder har opphav hos pytagoreerne, men det er ikke kjent nøyaktig når og hvordan kjennskap til slike størrelser ble etablert.<ref name=TH154>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.154-157 </ref> Historikeren [[Proklos]], som levde i det femte århundre etter Kristus, gir æren til Pytagoras selv, men ifølge Thomas Heath er det mest sannsynlig at kunnskapen oppstod en god stund etter at Pytagoras var død. En av flere alternative historier om pytagoreeren [[Hippasos]] et at han ble druknet, etter å ha røpet kunnskapen om inkommensurable størrelser.<ref name=TH65>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.65 </ref> |
|||
punkter i planet, så er distansen mellom dem, også kalt den ''euklidske avstanden'', gitt ved: |
|||
Euklid bruker bok X til å diskutere inkommensurable lengder og areal.<ref name=TH402>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.402ff </ref> |
|||
=== Distanse i euklidske rom === |
|||
:<math> \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2}. </math> |
|||
[[Metrikk]]en eller avstandsmålet i euklidsk geometri er basert på Pytagoras' teorem. Hvis <math>a = (x_1,y_1)</math> og <math>b = (x_2, y_2)</math> er [[Kartesisk koordinatsystem|kartesiske koordinater]] til to punkt i planet, så er avstanden mellom disse gitt ved |
|||
:<math>d(a,b) = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}. </math> |
|||
Mer generelt vil, i et euklidsk n-dimensjonalt rom, den euklidske avstanden mellom to punkter være: <math>\scriptstyle A\,=\,(a_1,a_2,\dots,a_n)</math> og <math>\scriptstyle B\,=\,(b_1,b_2,\dots,b_n)</math>, gitt ut fra Pythagoras' teorem, ved: |
|||
Dette avstandsmålen kalles ''euklidsk avstand'' eller ''euklidsk metrikk''. |
|||
:<math>\sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2} = \sqrt{\sum_{i=1}^n (a_i-b_i)^2}.</math> |
|||
I et generelt [[euklidsk rom|euklidsk n-dimensjonalt rom]] er avstanden mellom to vektorer <math>v_1 = (a_1,a_2,\dots,a_n)</math> og <math>v_2 = (b_1,b_2,\dots,b_n)</math> definert ved |
|||
== Generalisering == |
|||
=== Likedannede figurer === |
|||
[[Fil:Pythagoras-for similar triangles.svg|thumb|En generalisering med likedannede triangler.<br />Grønt {{Nowrap|areal {{=}} rødt}} areal]] |
|||
:<math>d(v_1,v_2) = \sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2} = \sqrt{\sum_{i=1}^n (a_i-b_i)^2}.</math> |
|||
Pythagoras' læresetning ble generalisert av Euklid i hans verk ''Elementene'' som: |
|||
=== Bruk i kompleks analyse === |
|||
{{Sitat|''Hvis en reiser likedannede figurer på sidene av et rett triangel, så er summen av arealene på de to minste sidene lik arealet av figuren på den største siden.''}} |
|||
[[Fil:Complex picture.svg|right|thumb|Absoluttverdien av et komplekst tall ''z'' svarer til avstanden ''r'' fra ''z'' til origo]] |
|||
=== Cosinussetningen === |
|||
Et vilkårlig [[komplekst tall]] kan skrives på formen |
|||
Pythagoras' teorem er et spesialtilfelle av et mer generelt teorem som omhandler lengden av sidene i et vilkårlig triangel, kjent som [[cosinussetningen]] eller ''den utvidede pytagoreiske læresetning'': |
|||
: |
:<math>z = x + iy.</math> |
||
:hvor θ er vinkelen mellom sidene med lengde ''a'' og ''b''. |
|||
:Når θ er 90 grader, er cos(θ) = 0. Dette reduserer formelen til den vanlige pytagoreiske læresetning. |
|||
Absoluttverdien eller modulus til dette tallet er definert ved<ref>{{Kilde bok| forfatter=R.V Churchill, J.W. Brown, R.F. Verhey| utgivelsesår=1974| tittel=Complex variables and applications| utgivelsessted=Tokyo| forlag=McGraw-Hill Kogakusha| side=7| isbn=0-07-010855-2 }}</ref> |
|||
=== Indreprodukt === |
|||
Gitt to [[vektorrom|vektorer]] '''v''' og '''w''' i et [[Komplekst tall|komplekst]] [[indreprodukt]]. Da kan Pythagoras' sats ta følgene form: |
|||
::<math>\|\mathbf{v}+\mathbf{w}\|^2 = \|\mathbf{v}\|^2 + \|\mathbf{w}\|^2 + 2\,\mbox{Re}\,\langle\mathbf{v},\mathbf{w}\rangle.</math> |
|||
:<math>r = |z|=\sqrt{x^2 + y^2}.</math> |
|||
eller, dersom '''v''' and '''w''' er [[Ortogonalitet|ortogonale]]: ||'''v''' + '''w'''||<sup>2</sup> = ||'''v'''||<sup>2</sup> + ||'''w'''||<sup>2</sup> Det inverse er imidlertid ikke alltid sant. |
|||
Sammenhengen mellom de tre størreslene <math>r</math>, <math>x</math> og <math>y</math> er gitt ved Pytagoras' ligning: |
|||
Gjennom [[matematisk induksjon]] kan det foregående utvides til et sett av parvis ortogonale vektorer: |
|||
:<math>r^2 = x^2 + y^2.</math> |
|||
La '''v'''<sub>1</sub>, '''v'''<sub>2</sub>, ..., '''v'''<sub>''n''</sub> være vektorer i et indreprodukt slik at <'''v'''<sub>''i''</sub>, '''v'''<sub>''j''</sub>> = 0 for 1 ≤ ''i'' < ''j'' ≤ ''n''. Da er: |
|||
::<math>\left\|\,\sum_{k=1}^{n}\mathbf{v}_k\,\right\|^2 = \sum_{k=1}^n \|\mathbf{v}_k\|^2.</math> |
|||
Absoluttveriden <math>r</math> er alltid definert positiv, selv om <math>x</math> og <math>y</math> kan ha både positive og negative verdier. Geometrisk er <math>r</math> avstanden fra origo til <math>z</math> i det komplekse planet. |
|||
En ytterligere generalisering er kjent som [[Parsevals sats]]. |
|||
Avstanden mellom to komplekse tall <math>z_1</math> og <math>z_2</math> kan defineres ved |
|||
Dersom formen ovenfor med vektorer anvendes i et tre-dimensjonalt rom kan dette utformes slik. Hvis linjene AB og BC danner en rett vinkel i B og linjene BC og CD danner en rett vinkel i C og linjen CD står vinkelrett på planet som inneholder linjene AB og BC, da er summen av kvadratene dannet av lengden av AB, BC og CD lik kvadratet av lengden av AD. |
|||
:<math>|z_1 - z_2|=\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}.</math> |
|||
=== Guas teorem === |
|||
En annen generalisering av Pythagoras' læresetning til tre dimensjoner er gitt i [[de Guas teorem]] etter [[Jean Paul de Gua de Malves]]: |
|||
<blockquote> |
|||
Hvis et [[tetraeder]] har et rettvinklet hjørne (hjørne som i en [[Kube|kubus]]), så er kvadratet av arealet på den motstående side til den rette vinkel lik summen av kvadratet av arealene på de andre tre sidene. |
|||
</blockquote> |
|||
Denne avstanden og de to gitte tallene er igjen relatert ved en ligning tilsvarende Pytagoras' ligning: |
|||
=== Pythagoras' læresetning innen ikke-euklidsk geometri === |
|||
Pythagoras' læresetning er basert på aksiomer innen [[euklidsk geometri]]. Innen [[ikke-euklidsk geometri]] holder ikke den euklidske formen. |
|||
:<math>|z_1 - z_2|^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2.</math> |
|||
For eksempel innen [[sfærisk geometri]]: Alle tre sidene i den rettvinklede trekanten som danner overflaten på en oktant i en enhetskule har sider lik <math>\scriptstyle \pi/2</math>. |
|||
Dette bryter med det euklidske pytagoreiske teorem ved at <math>\scriptstyle (\pi/2)^2+(\pi/2)^2\neq (\pi/2)^2</math>. |
|||
=== Den pytagoreiske trigonometriske identiteten === |
|||
Dette innebærer at innen ikke-euklidsk geometri må Pythagoras' teorem uttrykkes annerledes enn den klassiske euklidske formen. Det er to aktuelle eksempler: innen sfærisk geometri og inne [[hyperbolsk geometri]]. |
|||
[[Fil:Trig functions.svg|thumb|Formlike rettvinklede trekanter med sinus og cosinus til en vinkel θ]] |
|||
For en rettvinklet trekant, som vist nederst i figuren til høyre, kan de [[Trigonometrisk funksjon|trigonometriske funksjonene]] sinus og cosinus defineres ved |
|||
:<math> |
|||
For enhver rettvinklet trekant på en kule med radius ''R'' kan Pythagoras' teorem skrives som: |
|||
\begin{alignat}{2} |
|||
\sin \theta &= \frac{b}{c} \\ |
|||
\cos \theta &= \frac{a}{c} |
|||
\end{alignat} |
|||
</math> |
|||
Ved å bruke Pythagoras' teorem, følger det fra disse definisjonene at |
|||
:<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\,\cos \left(\frac{b}{R}\right).</math> |
|||
:<math>\sin^2 \theta + \cos^2 \theta = \frac{a^2 + b^2}{c^2} = 1 </math> |
|||
Ved å uttrykke cosinusfunksjonen som en [[Taylorrekke|maclaurinrekke]] kan en vise at når radien ''R'' øker mot uendelig, vil den sfæriske formen på Pythagoras' teorem gå mot den euklidske formen (idet kuleflaten nærmer seg en plan flate). |
|||
Denne grunnleggende identiteten blir kalt [[enhetsformelen]] og noen ganger også ''den pytagoreiske trigonometriske identiteten''.{{tr}} For to formlike trekanter er forholdet mellom samsvarende sidelengder det samme, |
|||
Innen hyperbolsk geometri kan en vise at teoremet kan uttrykkes som: |
|||
og dette vil også gjelde for de to trekantene i figuren. Den øverste rettvinklet trekanten har hypotenusen med lengde 1, og katetene har lengde <math>\sin \theta</math> og <math>\cos \theta</math>. |
|||
== Generaliseringer == |
|||
:<math> \cosh c=\cosh a\,\cosh b</math> |
|||
=== Cosinussetningen === |
|||
Ved å rekkeutvikle den hyperbolske funksjonen som en maclaurinrekke vil (når man tar med de to første leddene) <math>\cosh x \approx 1 + x^2/2</math>. Det kan da vises at når et hyperbolsk triangel blir lite (altså når ''a'', ''b'' og ''c'' alle går mot null), vil den hyperbolske formen av teoremet gå mot den euklidske formen. |
|||
[[Fil:Triangle.Acute.png|thumb|Spissvinklet trekant]] |
|||
[[Fil:Triangolo-Ottuso.png|thumb|Stumpvinklet trekant]] |
|||
Pytagoras' teorem er et spesialtilfelle av et mer generelt teorem om forholdet mellom sidelengder i en vilkårlig trekant, kjent som [[cosinussetningen]] eller ''den utvidede pytagoreiske læresetning''.<ref name=EJW85>{{kilde bok | tittel=Plane trigonometry and applications |forfatter=Ernest Julius Wilczynski, Herbert Ellsworth Slaught |url=https://archive.org/details/planetrigonomet00wilcgoog |år=1914 |forlag=Allyn and Bacon |side=85ff}}</ref><ref>{{Kilde bok |utgivelsesår = 1986 |tittel = Matematikk for den videregående skole |isbn = 82-05-16032-5 |utgivelsessted = Oslo |forlag = Gyldendal |url = http://urn.nb.no/URN:NBN:no-nb_digibok_2014073005007 | side =25 }}</ref> |
|||
For en vilkårlig trekant med sidelengder <math>a</math>, <math>b</math> og <math>c</math> er |
|||
:<math>a^2+b^2-2ab\cos{\gamma}=c^2 </math>. |
|||
=== Innen kompleks aritmetikk === |
|||
Pythagoras' formel gjelder for å finne avstanden mellom to punkter i kartesisk koordinatsystem og er gyldig dersom alle koordinater er reelle tall: avstanden mellom punktene (''a'', ''b'') og (''c'', ''d'') er <math> \sqrt{(a - c)^2 + (b - d)^2}\,</math>. |
|||
Her er <math>\gamma</math> vinkelen mellom sidene med lengde <math>a</math> og <math>b</math>. For <math>\gamma</math> lik 90 grader er <math>\cos \gamma = 0</math>, og ligningen reduserer seg til den vanlige |
|||
Med [[Komplekst tall|komplekse koordinater]] fungerer teoremet ikke. For eksempel vil avstanden mellom punktene {0,1} og {''i'',0} komme ut som 0, noe som er et ''[[reductio ad absurdum]]''. Dette fordi formelen baserer seg på Pythagoras' teorem der alle bevis baseres på arealer av geometriske figurer der grenselinjene skiller mellom en innside og en utside, noe som ikke holder dersom koordinatene er komplekse. |
|||
pytagoreiske ligningen. |
|||
Cosinussetningen gir en enkel metode for å bestemme om en trekant er rett, spissvinklet eller stumpvinklet, Siden cosinus-funksjonen er positiv for en spiss vinkel, men negativ for en stump vinkel, så gjelder følgende: |
|||
For avstanden mellom punktene (''a'', ''b'') og (''c'', ''d'') er det vanlig å la: |
|||
* <math>a^2 + b^2 = c^2</math> hvis og bare hvis trekanten er rettvinklet. |
|||
:(''p'' og ''q'' være den reelle og den imaginære del av (''a'' − ''c'')) |
|||
* <math>a^2 + b^2 < c^2</math> hvis og bare hvis trekanten er spissvinklet. |
|||
:(''r'' og ''s'' være den reelle og den imaginære del av (''b'' − ''d'')) |
|||
* <math>a^2 + b^2 > c^2</math> hvis og bare hvis trekanten er stumpvinklet. |
|||
: <math> |
|||
\begin{align} |
|||
Her er forutsatt at <math>c</math> er den lengste siden. En vanlig notasjon er å la vinklene i trekanten være <math>\alpha, \beta, \gamma</math>, slik at <math>\alpha</math> er motstående til sidelengden <math>a</math> og <math>\beta</math> motstående til |
|||
& {}\qquad \sqrt{(p+iq)\overline{(p+iq)} + (r+is)\overline{(r+is)}} \\ |
|||
sidelengden <math>b</math>. Forholdene over kan da også uttrykkes slik: |
|||
& = \sqrt{(p+iq)(p-iq) + (r+is)(r-is)} \\ |
|||
& = \sqrt{p^2 + q^2 + r^2 + s^2} |
|||
* I en spissvinklet trekant er <math>\alpha + \beta > \gamma</math> og <math>a^2 + b^2 < c^2</math>. |
|||
\end{align} |
|||
* I en stumpvinklet trekant er <math>\alpha + \beta < \gamma</math> og <math>a^2 + b^2 > c^2</math>. |
|||
[[Edsger Dijkstra]] har samlet disse resultatene ved hjelp av [[Signum (matematikk)|fortegnsfunkjonen]]:<ref>{{kilde www||url=http://www.cs.utexas.edu/users/EWD/ewd09xx/EWD975.PDF |tittel=On the theorem of Phytagoras |utgiver=Edsger Dijkstra, University of Texas | besøksdato=2021-03-13}}</ref> |
|||
:<math>\sgn(\alpha + \beta - \gamma) = \sgn(a^2 + b^2 - c^2)</math> |
|||
=== Parallellogramloven === |
|||
[[Image:Color parallelogram.svg|right|thumb|Sider i et parallellogram vist i blått og diagonalene i rødt]] |
|||
[[Parallellogramloven]] er en generalisering av Pytagoras' sats til et vilkårlig parallellogram, tilskrevet [[Apollonios fra Perge]].<ref name=AH309>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.309 </ref> |
|||
: <math>2(AB)^2+2(BC)^2=(AC)^2+(BD)^2\ .</math> |
|||
For et rektangel er de to diagonalene like lange: <math>AC = BD</math>, og parallellogramloven reduserer seg til Pytagoras’ læresetning. |
|||
=== Formlike figurer === |
|||
Pytagoras' læresetning kan tolkes som en relasjon mellom arealet til kvadrater på sidekantene. Ved å multiplisere alle tre leddene i Pytagoras' ligning med <math>\pi /8</math>, ser en umiddelbart at samme |
|||
relasjon også gjelder for arealene til halvsirkler med diameter langs sidekantene. Dette resultatet er referert uten bevis av [[Hippokrates fra Khíos]], som levde i det femte århundre før Kristus.<ref name=TH397>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.397 </ref> |
|||
Euklid viste i bok VI av ''Elementer'' et bevis for a resultatet gjelder for vilkårlige formlike [[konveks polygon|konvekse polygon]].<ref name=TH397/> I ettertid er det vist at resultatet er gyldig for vilkårlige formlike |
|||
figurer, også figurer der sider er definerte ved kurver:{{tr}} |
|||
:''«Hvis en reiser formlike figurer på sidene av et rett trekant, så er summen av arealene på de to minste sidene lik arealet av figuren på den største siden.»'' |
|||
De tre sidelengdene i den rette trekanten er lik sidelengder i de tilstøtende figurene, slik at disse må være formlike i forholdet <math>a:b:c</math>. Den grunnleggende idéen bak generaliseringen er at i formlike |
|||
figurer er forholdet mellom arealet og kvadratet av en vilkårlig karakteristisk lengde det samme: |
|||
:<math> |
|||
\begin{alignat}{2} |
|||
&\frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2} \\[7pt] |
|||
&\Rightarrow A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C = C |
|||
\end{alignat} |
|||
</math> |
</math> |
||
{| |
|||
hvor <math> \overline{z}\,</math> den [[Kompleks konjugasjon|komplekse konjugasjon]] av <math> z </math>. |
|||
| [[Fil:Pythagoras applied to similar triangles.svg|thumb|Generalisering med formlike trekanter. For arealene gjelder ''A'' + ''B'' = ''C'']] |
|||
For eksempel ville distansen mellom punktene (0, 1) og (''i'', 0) bli 0 hvis en ikke tok hensyn til kompleks konjugasjon, mens avstanden er: |
|||
| [[Fil:Pythagoras by pentagons.svg|thumb|Generalisering med regulære pentagoner]] |
|||
|} |
|||
=== Pappos arealteorem === |
|||
: <math> \sqrt{i\cdot\overline{i} + 1 \cdot\overline{1}} = \sqrt{2} \, </math> |
|||
[[Pappos fra Alexandria|Pappos]] (3-4. århundre) gir et ''arealteorem'' han selv kaller en utviding av Euklid I.47.<ref name=TH369>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. II) s.369-371 </ref> |
|||
Dersom en på to sider i en vilkårlig trekant tegner to vilkårlige parallellogram, så kan en konstruere et parallellogram på den tredje siden, slik at arealet av dette er lik summen |
|||
av arealene til de to første. |
|||
{| |
|||
| [[Fil:Pappus area theorem proof2.svg|thumb|Pappos' arealteorem: Summen av de to mørkegrå arealene er lik det lysegrå arealet]] |
|||
|} |
|||
===Romgeometri === |
|||
[[Fil:Pythagoras 3D.svg|thumb|Euklidsk avstand i rommet]] |
|||
En lengde i det tredimensjonale rommet kan defineres ved gjentatt bruk av Pytagoras' setning. I figuren til høyre kan en finne lengden av linjestykket <math>AD</math> ved å bruke den rettvinklede trekanten <math>ABD</math>: |
|||
:<math> AD^2 = AB^2 + BD^2 \ .</math> |
|||
Kateten <math>BD</math> i denne er gitt ved å bruke Pytagoras' sats på trekanten <math>BCD</math>: |
|||
:<math> BD^2 = BC^2 + CD^2 \ .</math> |
|||
Kombinasjon av disse to ligningene gir |
|||
:<math> AD^2 = AB^2 + BC^2 + CD^2 \ .</math> |
|||
Resultatet er det tredimensjonale uttrykket for lengden av en vektor <math>\mathbf{v} = (v_1, v_2, v_3)</math>, basert på komponentene. Vektoren svarer til diagonalen <math>AD</math> |
|||
:<math>\|\mathbf{v}\|^2 = \sum_{i=1}^3 v_i^2.</math> |
|||
=== de Guas teorem === |
|||
I tre romdimensjoner er [[de Guas teorem]] en generalisering av Pytagoras' læresetning til et [[tetraeder]]:<ref>{{kilde www| url=https://mathworld.wolfram.com/deGuasTheorem.html |tittel=De Gua's theorem |utgiver=Wolfram MathWorld |besøksdato=2021-03-14}}</ref> |
|||
:''«Hvis et tetraeder har et rettvinklet hjørne, så er kvadratet av arealet på den motstående side til den rette vinkel lik summen av kvadratene av arealene på de tre andre sidene.»'' |
|||
Et rettvinklet hjørne er som hjørnet i en [[kube]]. Teoremet er navngitt etter [[Jean Paul de Gua de Malves]] (1713-1785). |
|||
=== Indreproduktrom === |
|||
Pytagoras' sats kan generaliseres til et vilkårlig [[indreprodukt]]rom, som igjen er en generalisering av det euklidske rommet i to og tre dimensjoner.<ref name=MILNE>{{Kilde bok| forfatter= Ronald Douglas Milne| utgivelsesår=1980| tittel=Applied functional analysis, an introductory treatment| utgivelsessted= London| forlag= Pitman Publishing Limited| isbn=0-273-08404-6 }}</ref> |
|||
Et indreproduktrom kan ha både endelig og uendelig dimensjon. Elementene i et indreproduktrom, [[vektor]]ene, kan for eksempel være [[funksjon (matematikk)|funksjoner]]. |
|||
I et indreproduktrom kan en definere lengden av elementer, avstanden mellom to elementer og også vinkelen mellom to elementer. |
|||
Indreproduktet mellom to elementer <math>\mathbf{u}</math> og <math>\mathbf{v}</math> kan betegnes som <math>\langle \mathbf{u},\mathbf{v} \rangle</math>, og dette generaliserer det vanlige skalarproduktet mellom to endelig-dimensjonale vektorer. |
|||
To vektorer står [[ortogonalitet|ortogonalt]] på hverandre dersom indreproduktet mellom dem er lik null. Lengden av en vektor er definert ved [[norm (matematikk)|normen]]: |
|||
:<math>\| \mathbf{u} \| = \sqrt{\langle \mathbf{u},\mathbf{u}\rangle} \, .</math> |
|||
I et indreproduktrom sier Pytagoras' teorem at for to ortogonale vektorer <math>\mathbf{u}</math> og <math>\mathbf{v}</math> gjelder at |
|||
:<math>\|\mathbf{u}+\mathbf{v}\|^2 = \|\mathbf{u}\|^2 + \|\mathbf{v}\|^2 \ .</math> |
|||
Vektorene <math>\mathbf{u}</math> og <math>\mathbf{v}</math> spiller samme rolle som katetene i en rettvinklet trekant, med hypotenusen gitt som vektorsummen <math>\mathbf{u} + \mathbf{v}</math>. |
|||
Teoremet følger av egenskaper til indreproduktet: |
|||
:<math>\left\| \mathbf{u} + \mathbf{v} \right\|^2 =\langle \mathbf{ u+v},\ \mathbf{ u+v}\rangle = \langle \mathbf{u},\ \mathbf{ u}\rangle +\langle \mathbf{v},\ \mathbf{v}\rangle +\langle\mathbf{ u,\ v }\rangle + \langle\mathbf{ v,\ u }\rangle \ = \left\| \mathbf{u}\right\|^2 + \left\| \mathbf{v}\right\|^2 . </math> |
|||
Ligningen kan generaliseres til et vilkårlig endelig antall parvis ortogonale vektorer: |
|||
:<math>\left\|\,\sum_{k=1}^{n}\mathbf{u}_k\,\right\|^2 = \sum_{k=1}^n \|\mathbf{u}_k\|^2.</math> |
|||
Også parallellogramloven kan generaliseres til et vilkårlig indreproduktrom, da med formen |
|||
::<math>2\|\mathbf{u}\|^2 +2 \|\mathbf{v}\|^2 = \|\mathbf {u + v} \|^2 +\| \mathbf{u-v}\|^2 \ . </math> |
|||
=== Differensialgeometri === |
|||
I [[differensialgeometri]] blir det for det tredimensjonale euklidske rommet definert en infinitesimal lengde <math>ds</math> ved<ref>{{Kilde bok| forfatter= D.J. Struik| utgivelsesår=1961| tittel=Lectures on classical differential geometry| utgivelsessted=New York| forlag=Dover Publications| side=5-10| isbn=0-486-65609-8 }}</ref> |
|||
:<math>ds^2 = dx^2 + dy^2 + dz^2</math>. |
|||
Dette svarer til bruk at Pytagoras' setning for en infinitesimal avstand mellom to punkt. For en glatt parametrisk kurve gitt på formen |
|||
:<math>\mathbf{r}(t) = x(t)\mathbf{i}+ y(t)\mathbf{j} + z(t)\mathbf{k} \qquad t \in [a,b] \, </math> |
|||
brukes dette til å definere [[buelengde]]n av kurven: |
|||
:<math>L = \int_a^b \sqrt{ x'^2 + y'^2 + z'^2} \; dt \ . </math> |
|||
=== Ikke-euklidsk geometri === |
|||
Pytagoras' setning er basert på aksiomer i euklidsk geometri, og den euklidske formen er ikke gyldig i [[ikke-euklidsk geometri]]. I |
|||
[[sfærisk geometri]] vil for eksempel alle tre sidene i en rettvinklet trekant som begrenser en oktant i en enhetskule, ha sidelengder <math>\pi/2</math>. |
|||
Dette bryter opplagt med Pytagoras' ligning. |
|||
For ikke-euklidsk geometri kan en utlede alternative former for Pytagoras' teorem. I sfærisk geometri gjelder det at |
|||
for enhver rettvinklet [[sfærisk trekant]], på en kule med radius <math>R</math>, kan Pytagoras' teorem skrives som: |
|||
:<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\,\cos \left(\frac{b}{R}\right).</math> |
|||
Når radien <math>R</math> går mot uendelig, vil kuleflaten nærme seg en plan flate. Tilsvarende vil den sfæriske formen på Pytagoras' teorem gå mot den euklidske formen. |
|||
Dette kan vises ved å utvikle cosinus-leddene som [[Taylorrekke|maclaurinrekke]]r. |
|||
I en [[hyperbolsk geometri]] med uniform krumning <math>1 / R^2</math> kan Pytagoras' teorem uttrykkes som: |
|||
:<math> \cosh \frac{c}{R}=\cosh \frac{a}{R}\,\cosh \frac{b}{R}</math> |
|||
Ved å rekkeutvikle den hyperbolske funksjonen som en maclaurinrekke, vil (når man tar med de to første leddene) <math>\cosh x \approx 1 + x^2/2</math>. Det kan da vises at når en hyperbolsk trekant blir lite (altså når ''a'', ''b'' og ''c'' alle går mot null), vil den hyperbolske formen av teoremet gå mot den euklidske formen. |
|||
== Historie == |
== Historie == |
||
Historien om teoremet kan deles i fire distinkte punkter: kunnskapen om pytagoreiske tripler, kjennskapen til sammenhengen mellom sidene i en [[Trekant|rett trekant]], kjennskap til sammenhengen mellom vinklene og teoremets bevis. |
|||
Opphavet og historien til Pytagoras' teorem har gjennom tidene skapt mye diskusjon, og mange teorier er fremsatt. Det kan i ettertiden være vanskelig å skille mellom fakta, tolkninger, grunngitte hypoteser og rene gjetninger. |
|||
[[Megalittisk monument|Megalittiske monumenter]] fra ca. 2500 år f.Kr. i [[Egypt]] og [[Nord-Europa]] inneholder rette triangler med heltallssider.<ref>{{Kilde www |
|||
Kanskje har kunnskapen om sammenhengen mellom trekantsidene oppstått på ulike steder til ulike tider, uavhengig av hverandre. |
|||
|url=http://hyperion.cc.uregina.ca/~astro/Mega_circ.html |
|||
Samtidig har mye kunnskap også blitt utvekslet på tvers av landegrenser og tidsepoker, uten at vi i dag har kjennskap til dette. At en forståelse av teoremet har eksistert svært lenge før |
|||
|tittel=Megalithic Monuments. |
|||
Pytagoras levde og virket, er nå allment akseptert.<ref name=AH26>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.26 </ref> Antagelig har forståelsen for teoremet vokst fram gjennom ulike |
|||
|besøksdato=2010-01-17 |
|||
stadier: en oppfatning av en rett vinkel, kunnskap om pytagoreiske tripler, kjennskap til sammenhengen mellom sidene i en rettvinklet trekant, kjennskap til sammenhengen mellom trekantvinkler og endelig teoremets bevis. |
|||
|arkiv-url=https://web.archive.org/web/20110706211316/http://hyperion.cc.uregina.ca/%7Eastro/Mega_circ.html |
|||
|arkivdato=2011-07-06 |
|||
Det er verdt å være oppmerksom på at bruk av begrep som «Pytagoras teorem» og «bevis» i forbindelse med oldtidens matematikk lett kan skape feil inntrykk. Et utsagn som |
|||
|død-lenke=ja |
|||
«xxx hadde et bevis for Pytagoras teorem tusen år før Pytagoras» kan som regel møtes med mange spørsmål, både når det gjelder kildebruk, tidsbestemmelse, formen på «teoremet» og kvaliteten av «beviset». |
|||
}}</ref> |
|||
Den nederlandske matematikeren [[Bartel Leendert van der Waerden]] gjetter på at disse pytagoreiske triplene ble funnet [[algebra]]isk.<ref>van der Waerden 1983.</ref> |
|||
=== I forhistorisk matematikk === |
|||
Oppmåling av europeiske og egyptiske [[Megalittiske monument|megalittiske monumenter]] fra ca. 2500 år f.Kr. har ført til at det er framsatt teorier om at steinene i disse monumentene er plassert |
|||
i former basert på rettvinklede trekanter med heltalssider.<ref>{{Kilde www|url=http://hyperion.cc.uregina.ca/~astro/Mega_circ.html |tittel=Megalithic monuments |besøksdato=2010-01-17|arkiv-url=https://web.archive.org/web/20110706211316/http://hyperion.cc.uregina.ca/%7Eastro/Mega_circ.html|arkivdato=2011-07-06|død-lenke=ja}}</ref> |
|||
Den nederlandske matematikeren [[Bartel Leendert van der Waerden]] gjetter på at de involverte pytagoreiske triplene ble funnet algebraisk.<ref>[[#WAE| B.L. van der Waerden: ''Geometry and algebra ...'']] s.??</ref> |
|||
=== I babylonsk matematikk === |
|||
{{utdypende|Babylonsk matematikk}} |
|||
[[Fil:Plimpton 322.jpg|thumb|Plimpton 322 med en tabell for pytagoreiske tripler]] |
|||
Funn av steintavler fra viser at [[Babylon|babylonerne]] var godt fortrolige med ulike former for algebra, inkludert beregning av pytagoreiske tripler.<ref name=AH21>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.21ff </ref> |
|||
Det har vært spekulert i hva babylonerne brukte de pytagoreiske triplene til, og en mulighet kan ha vært i løsning av systemer av andregradsligninger med to ukjente. |
|||
Babylonerne var også kjent med sammenhengen mellom en rettvinklet trekant og pytagoreiske tripler. |
|||
En svært viktig kilde til kunnskap er [[kileskrift]]tavlen [[Plimpton 322]] fra [[Mesopotamia]], skrevet i perioden 1822-1784 f.Kr.<ref name=AH21/> Den antas å stamme fra den babylonske byen [[Larsa]]. Tavlen inneholder en tabell |
|||
med fire kolonner og 15 rader. Kolonne nummer fire fra venstre nummererer radene, med tall fra 1 til 15. Kolonne nummer en er delvis ødelagt. Kolonne nummer to og tre har som overskrift henholdsvis |
|||
«Bredde» og «Diagonal». Tabellen er tolket som å inneholde tall brukt for å konstruere pytagoreiske tripler, inkludert de følgende: |
|||
:<math> |
|||
\begin{alignat}{2} |
|||
(56, 90, 106) \\ |
|||
(119, 120, 169) \\ |
|||
(12709, 13500, 18541) |
|||
\end{alignat} |
|||
</math>. |
|||
En slik tolkning viser at babylonerne hadde metoder til å regne ut triplene, og tallene i tavlen kan indikere at de kjente Diofants konstruksjonsmåte. |
|||
Et [[papyrus]] skrevet mellom 2000 og 1786 f.Kr. i [[Mellomriket i Egypt]] er i dag kjent som [[Berlinpapyrus 6619]]. Her fremsettes oppgaver der tripler inngår som løsning. |
|||
En annen tavle i kileskrift, fra [[Hammurabi|Hammurabi-dynastiet]] (1829–1530 f.Kr.), finnes nå i [[British Museum]].<ref name=BM1>{{kilde www |url=https://www.britishmuseum.org/collection/object/W_1899-0415-3 |tittel=Tablet 85196 |utgiver=British Museum |besøksdato=2021-03-14}}</ref> |
|||
En tavle i [[kileskrift]] fra [[Hammurabi]]dynastiet (1829–1530 f.Kr.) i [[Babylon]] finnes i [[British museum]] (artikkel 85196). Her er gjengitt et geometrisk problem med løsning utført i det [[sexagesimale tallsystem]]:<ref>Helmuth Gericke: ''Mathematik in Antike und Orient'', Berlin 1984, S. 33f.; Kurt Vogel: ''Vorgriechische Mathematik''. Teil II: ''Die Mathematik der Babylonier'', Hannover und Paderborn 1959, S. 67f.</ref> |
|||
Tavlen inneholder et geometrisk problem, med løsning gitt i det [[Seksagesimalsystem|seksagesimale tallsystem]]:<ref>[[#HG| H. Geriche: ''Mathematik in Antike und Orient '']] s.33f </ref><ref>[[#KV| K. Vogel: ''Vorgriechische Mathematik'']] s.67f </ref> |
|||
[[Fil:Pythagoras_Sexagesimal.gif|thumb|left|En stav med lengde 0;30 synker 0;6 ved at foten flyttes til siden. Hvor langt til siden flyttes fotpunktet?]] |
|||
[[Fil:Pythagoras_Sexagesimal.gif|thumb|left|En stav med lengde 0;30 senkes 0;6 ved at foten flyttes til siden. Hvor langt til siden flyttes fotpunktet?]] |
|||
{| |
{| |
||
| |
|||
|Et Pythagorasproblem fra ca. 1700 f.Kr. |
|||
|----- bgcolor="#DDDDDD" |
|----- bgcolor="#DDDDDD" |
||
! |
! |
||
| Linje 317: | Linje 480: | ||
|Originalteksten i oversettelse || Kommentarer |
|Originalteksten i oversettelse || Kommentarer |
||
|----- bgcolor="#EEEEEE" |
|----- bgcolor="#EEEEEE" |
||
| ''En stav: 0;30 GAR'' || 30/60 GAR = 1/2 GAR ≈ 3 m lang.<ref> |
| ''En stav: 0;30 GAR'' || 30/60 GAR = 1/2 GAR ≈ 3 m lang.<ref>[[#KV| K. Vogel: ''Vorgriechische Mathematik'']] s.20 </ref> |
||
|----- bgcolor="#EEEEEE" |
|----- bgcolor="#EEEEEE" |
||
| ''foroven er den sunket 0;6'' || Når toppen |
| ''foroven er den sunket 0;6'' || Når toppen er senket 6/60 |
||
|----- bgcolor="#EEEEEE" |
|----- bgcolor="#EEEEEE" |
||
| ''nedentil har den fjernet seg'' || ..hvor langt har foten fjernet seg fra vertikalen? |
| ''nedentil har den fjernet seg'' || ..hvor langt har foten fjernet seg fra vertikalen? |
||
| Linje 325: | Linje 488: | ||
| ''0;30 kvadrere: 0;15, skjønner?'' || (30/60)<sup>2</sup> = 900/3500 = 15/60 |
| ''0;30 kvadrere: 0;15, skjønner?'' || (30/60)<sup>2</sup> = 900/3500 = 15/60 |
||
|----- bgcolor="#EEEEEE" |
|----- bgcolor="#EEEEEE" |
||
| trekke 0;6 fra 0;30: 0;24, skjønner? || -6/60 + 30/60 = 24/60 |
| ''trekke 0;6 fra 0;30: 0;24, skjønner?'' || -6/60 + 30/60 = 24/60 |
||
|----- bgcolor="#EEEEEE" |
|----- bgcolor="#EEEEEE" |
||
| ''0;24 kvadrere: 0;9,36, skjønner?'' ||(24/60)<sup>2</sup> = 576/3600 = 0;9,36 |
| ''0;24 kvadrere: 0;9,36, skjønner?'' ||(24/60)<sup>2</sup> = 576/3600 = 0;9,36 |
||
| Linje 336: | Linje 499: | ||
|} |
|} |
||
{{Clear}} |
{{Clear}} |
||
Løsningen i tavlen kan skrives som: |
|||
:<math>0;18^2 = 0;30^2 - 0;24^2\ |
:<math>0;18^2 = 0;30^2 - 0;24^2\ .</math> |
||
Fra denne kilden fremgår imidlertid ikke om babylonerne kjente noe matematisk bevis. |
Dette svarer til Pytagoras' sats på formen <math> a^2 = c^2 - b^2</math>. Fra denne kilden fremgår imidlertid ikke om babylonerne kjente noe matematisk bevis. |
||
Ifølge historikeren [[Jamblikos]] skal Pytagoras ha oppholdt seg tolv år i Babylon.<ref name=AH169>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.169 </ref> |
|||
Kileskrifttavlen [[Plimpton 322]] fra [[Mesopotamia]] er skrevet i perioden 1822-1784 f.Kr og antas å stamme fra den [[babylon]]ske byen [[Larsa]]. Den inneholder 15 pytagoreiske tripler, deriblant: |
|||
:<math>(56, 90, 106)</math>, <math>(119, 120, 169)</math> og <math>(12709, 13500, 18541)</math>. |
|||
=== I egyptisk matematikk === |
|||
Dette tyder på at babylonerne hadde metoder til å regne ut slike tripler. |
|||
{{utdypende|Oldtidens egyptiske matematikk}} |
|||
En vanlig oppfatning er at egyptisk matematikk ikke nådde like langt som den babylonske, spesielt ikke innenfor algebra.<ref name=AH59>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.59ff </ref><ref name=BO40>[[#BOYER|C.B.Boyer: ''A history of mathematics'']] s.40 </ref> |
|||
Om de utviklet ''ny'' geometrisk kunnskap er omdiskutert.<ref name=BO40/> Gjennom landmåling la imidlertid egypterne et grunnlag for den etterfølgende greske geometrien, og egypterne har brukt |
|||
pytagoreiske tripler til hjelp for å konstruere rette vinkler. En tau-ring med tolv ekvidistante knuter kan brukes til å danne en trekant med sidene 3,4,5, og derved danne en rett vinkel. |
|||
Det er lite funn av direkte kilder om egyptisk kjennskap til den pytagoreiske læresetningen. Verken [[Moskva-papyrusen]] eller [[Rhind-papyrusen]] nevner problemstillinger der denne er i bruk. |
|||
I det indiske [[Śulbasūtraene]] (som er en del av ''[[Baudhayanasūtraene]]''), fra engang mellom det 8. og 2. århundre f.Kr. finner en fem tripler oppdaget algebraisk, en beskrivelse av teoremet og et geometrisk bevis med en likesidet trekant.<ref> |
|||
[[Berlinpapyrus 6619|Berlin-papyrus 6619]] er skrevet mellom 2000 og 1786 f.Kr. i [[Mellomriket i Egypt|Mellomriket]], og her forekommer fire ligninger som alle er basert på det pytagoreiske trippelet |
|||
Helmuth Gericke: ''Mathematik in Antike, Orient und Abendland'', Wiesbaden 2005, S. 68; |
|||
(3,4,5):<ref>{{kilde bok| forfatter=Stephen Hawking |tittel=God created the integers: The mathematical breakthroughs that changed history |forlag=Greenworld Books |år=2005 |isbn=978-0762419227 |url=https://books.google.no/books?id=Lu83DgAAQBAJ&pg=PT23&lpg=PT23#v=onepage&q&f=false}}</ref> |
|||
</ref> |
|||
<ref> |
|||
Oskar Becker, ''Das mathematische Denken der Antike'', Göttingen 1966, S. 55f. |
|||
</ref> |
|||
<ref> |
|||
Thomas L. Heath, ''The thirteen books of Euclid's Elements'', Bd. 1, 2. Auflage, New York 1956, S. 360-364.</ref> |
|||
:<math> |
|||
''Apastamba-Sulba-Sutra'' fra ca. 600 f.Kr. inneholder et numerisk bevis for teoremet basert på arealbetraktninger. Van der Waerden tror at «dette er med sikkerhet basert på tidligere tradisjon». Ifølge Albert Bŭrk er dette det originale beviset for teoremet. Han gjør seg videre de antagelser at Pythagoras besøkte [[Arakkonam]] i India og kopierte beviset. |
|||
\begin{alignat}{2} |
|||
1^2 + ( \frac{3}{4} )^2 &= ( 1\frac{1}{4} )^2 \\ |
|||
8^2 + 6^2 &= 10^2 \\ |
|||
2^2 + ( 1\frac{1}{2} )^2 &= ( 2\frac{1}{2} )^2 \\ |
|||
16^2 + 12^2 &= 20^2 |
|||
\end{alignat} |
|||
</math> |
|||
Papyrusen inneholdet imidlertid ingen referanse til trekanter. |
|||
[[Fil:Chinese pythagoras.jpg|thumb|Grafisk bevis for en (3, 4, 5) trekant, gjengitt i ''Zhoubi suanjing'' 500–200 f.Kr.]] |
|||
Læresetningen var tidlig kjent i Kina under navnet ''Gōugŭ'' (勾股), «base og høyde». For et triangel med sidene 3, 4 og 5 ble læresetningen kalt ''Gōugŭ-teoremet'' (勾股定理, Gōugŭ Dìnglĭ). |
|||
Mye av kunnskapen om egyptisk geometri kommer fra greske kilder.<ref name=TH123>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.123ff</ref> |
|||
Den kinesiske teksten ''[[Zhoubi suanjing]]'' (周髀算经, «Den aritmetiske klassiker om Gnomon og himmelens sirkulære veier»), som ble skrevet en gang mellom 500 f.Kr. og 200 e.Kr., gjengir 246 løsninger på matematiske problemer. I diagrammet ''hsuan-shu'' gjengir teksten et visuelt og grafisk bevis på den pythagoreiske læresetning for en trekant med sider 3, 4 og 5.<ref>Oskar Becker, ''Das mathematische Denken der Antike'', Göttingen 1966, S. 56.</ref> Figuren er gjengitt til høyre. Den vertikale teksten til venstre for figuren lyder: ''gōu gǔ mì hé yǐ chéng xián mì'' (勾股幂合以成弦幂), som betyr: «Summen av lengdene til kvadratene til høyden og basen er lik lengden til hypotenusen.» |
|||
Den antikke historikeren [[Herodot]] forteller om egyptisk landmåling og gir dette æren for opphavet til geometri. |
|||
Proklos forteller at grekeren [[Thales]] reiste til Egypt og lærte geometri der. |
|||
Også Pytagoras skal ha vært på reise i Egypt.<ref name=AH169/> |
|||
[[Demokrit]] skryter av at ingen har overgått ham i geometrisk kunnskap, ikke en gang de egyptiske «tau-strekkerne».<ref name=TH123/> |
|||
=== I indisk matematikk === |
|||
''[[Chiu chang suan shu]]'' («Ni kapitler om den matematiske kunst»), et klassisk matematisk verk fra Kina satt sammen fra det 10. til det 2. århundre f.Kr., gjengir 263 løsninger på matematiske problemer. I kapittel 9 omtales pytagoreiske tripler og rette triangler.<ref>Swetz.</ref> I boken ''[[Jiuchang suan shu]]'', en kommentar til «[[Ni kapitler om den matematiske kunst|Ni kapitler]]» som ble skrevet av [[Liu Hui]] i året 263 e.Kr., blir det gitt et bevis i kapittel 9.<ref>Karine Chemla, Guo Shuchun, ''Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Édition critique.'' s. 680</ref> |
|||
{{utdypende|Indisk matematikk}} |
|||
[[File:Pythagoras sulbasutram50.png|thumb|Geometri i Sutra 50]] |
|||
[[Śulbasūtraene]] er en samling av indiske [[sutra|sutra-tekster]] fra engang mellom det 8. og 2. århundre f.Kr. Dette verket er en del av en større samling av religiøse tekster, |
|||
og delen omtaler matematikk for å kunne konstruere brennalter og for å sette opp en kalender over religiøse høytider<ref name=SV>{{kilde bok|forfatter=Swami Vishnu |tittel=Vedic science & history |forlag=Gosai Publishers |år=2018 |isbn=978-8-1926601-3-4 |side=65f}}</ref> |
|||
Tittelen kan oversettes med «Regler for bruk av snoren».<ref name=AH122>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.122 </ref> |
|||
Teksten lister fem pytagoreiske tripler, gir en form for Pytagoras' teorem og viser i tillegg at teoremet er gyldig for en likesidet trekant.<ref>[[#HG| H. Geriche: ''Mathematik in Antike und Orient '']] s.68</ref><ref name=OB>{{kilde bok |forfatter=Oskar Becker |tittel=Das mathematische Denken der Antike |forlag=Vandenhoeck & Ruprecht |utgivelsessted=Göttingen |år=1966 |side=55f}}</ref><ref>[[#EUKLID| Euclid: ''The thirteen books of...'']] s.360-364</ref> |
|||
Der eksisterer minst fire versjoner av Sulbasutraene, men geometri-beskrivelsen er relativt like i disse fire.<ref name=DWH>{{kilde bok| tittel=Experiencing geometry |forfatter=David W. Henderson, Daina Tamina |forlag=Project Euclid |isbn=978-0131437487 |url=https://projecteuclid.org/ebooks/books-by-independent-authors/Experiencing-Geometry/chapter/Chapter-13-Square-Roots-Pythagoras-and-Similar-Triangles/10.3792/euclid/9781429799850-17 |side=174ff}}</ref> |
|||
Pythagoras, som antas å ha levd i årene 569-475 f.Kr., brukte algebraiske metoder for å konstruere pytagoreiske tripler ifølge [[Proklos]] (410-485 e.Kr.) idet han kommenterer Euklid. Ifølge [[Thomas Heath|Sir Thomas L. Heath]] ble ikke teoremet omtalt med noen referanse til Pythagoras i løpet av femhundre år, men når [[Platon]] og [[Cicero]] tilskriver teoremet til Pythagoras, gjør de det på en måte gir uttrykk for at dette er anerkjent og uomtvistet.<ref name="Heath, Vol I, p. 144" /> |
|||
Versjonen som skal være laget av Baudhayana er anslått å være fra omkring 600 f.Kr, det vil si rundt hundre år før Pytagoras. Mye tyder på at kunnskapen som er samlet i teksten kan være betydelig eldre. |
|||
Baudhayana-Sulbasutra drøfter flere problem der oppgaven er å konstruere en figur med samme areal som en eller flere andre figurer. I Sutra 50 gir teksten en oppskrift for å summere arealet av to kvadrat, illustrert ved figuren til høyre: |
|||
{{sitat|Hvis du vil slå sammen to ulike kvadrater til ett, ta det største kvadratet og legg til et bit av det største.Biten skal være laget med en side lik siden i det minste kvadratet. Diagonalen i denne biten er siden i det kombinerte kvadratet.|Baudhayana Sutra 50<ref name=DWH/>}} |
|||
Det diskuteres om hvorvidt teoremet ble oppdaget én eller flere ganger. Boyer (1991) hevder at enkelte elementer i ''Shulba Sutra'' kan være av [[Mesopotamia|mesopotamisk]] opprinnelse.<ref name="Boyer207" /> |
|||
Sutra 50, 51 og 54 gir sammen en form for godtgjøring for at Pytagoras' sats er riktig. Om dette kan gjelde som et generelt «bevis» er omdiskutert.<ref name=DWH/><ref name=TH144/> |
|||
=== Pythagoras' rolle === |
|||
[[Fil:Kapitolinischer Pythagoras adjusted.jpg|thumb|Byste av Pythagoras i de Kapitolske museer i [[Roma|Rom]].]] |
|||
At teoremet har navn etter den greske [[filosof]]en [[Pythagoras]] fra det [[6. århundre f.Kr.]] fremgår kun av de senere kildene. Forskerne strides om hans faktiske rolle og flere hypoteser finnes: |
|||
* Pythagoras overtok satsen fra babylonerne. Han var kun en formidler av orientalsk kunnskap til grekerne. Dette er synet til vitenskapshistorikeren [[Walter Burkert]].<ref> |
|||
Walter Burkert, ''Weisheit und Wissenschaft'', Nürnberg 1962, S. 405f., 441ff. |
|||
</ref> Ifølge antikke kilder foretok han en reise til [[Egypt]] og muligens til Babylon, men troverdigheten til disse beretningene er omstridt. |
|||
* En utbredt oppfatning i antikken var at Pythagoras selv oppdaget og beviste satsen uavhengig av orientalsk matematikk. Dette er også synet til vitenskapshistorikeren [[Leonid Zhmud]].<ref> |
|||
Leonid Zhmud, ''Wissenschaft, Philosophie und Religion im frühen Pythagoreismus'', Berlin 1997, S. 141-151, 160-163.</ref><ref>Thomas L. Heath, ''The thirteen books of Euclid's Elements'', Bd. 1, 2. Auflage, New York 1956, S. 350-360.</ref> |
|||
* Pythagoras støttet seg til orientalske kilder, men var den første som fant et bevis. Egypterne og babylonerne var primært interessert i satsens anvendelse og ikke et generelt bevis. Egypteren Ahmes regnebok fra de 17. århundre f.Kr., den eldste kjente regnebok i verden, også kjent som ''[[Papyrus Rhind]]'', inneholder en rekke kompliserte oppgaver. Det inngår imidlertid ingen generaliteter, definisjoner eller bevis. |
|||
* Kanskje hadde ikke Pythagoras noen påvirkning. Pytagoreere kan på et senere tidspunkt ha funnet et bevis og ved en tilfeldighet knyttet dette til Pythagoras. |
|||
Det er blitt foreslått at inderne hentet kunnskap fra Mesopotamia,<ref name=BO229>[[#BOYER|C.B.Boyer: ''A history of mathematics'']] s.229 </ref> men også motsatt, at Mesopotamia fikk kunnskap fra India.<ref name=DWH/> |
|||
Euklid dokumenterer i sitt verk ''Elementene'' fra siste halvdel av det 4. århundre e.Kr. den matematiske kunnskap fra sin tid. Han fremlegger et bevis, men gir ingen referanse til Pythagoras. Det eldste belegg en har for en mulig sammenheng finner en i form av et [[epigram]] etter en Apollodoros. Dette kan være filosofen Apollodoros fra Kyzikos. I så fall stammer det fra siste halvdel av det 4. århundre f.Kr. og lyder: |
|||
{{Sitat|''Da Pythagoras, som første, den berømte tegningen fant,<br /> |
|||
=== I kinesisk matematikk === |
|||
han brakte da som offer et guddommelig oksedyr.''}} |
|||
{{utdypende|Kinesisk matematikk}} |
|||
[[Fil:Chinese pythagoras.jpg|thumb|Grafisk bevis for en (3, 4, 5) trekant, gjengitt i ''Zhoubi suanjing'']] |
|||
Også kinesisk matematikk har i lang tid kjent til former for Pytagoras' teorem. |
|||
Den eldste kjente kinesiske matematiske teksten er antagelig ''[[Soluret og himmelens sirkler|Zhoubi suanjing]]'' (''Soluret og himmelens sirkler'').<ref name=BO217>[[#BOYER|C.B.Boyer: ''A history of mathematics'']] s.217 </ref> |
|||
Tidfestingen av gamle kinesiske matematiske verk er svært usikker, og datering varierer sterkt i ulike kilder. Historien til ''Zhoubi suanjing'' kan gå helt tilbake til 1200 f.Kr, men verket har kanskje fått |
|||
en endelig form en gang mellom 500 f.Kr. og 200 e.Kr. Innholdet er astronomiske beregninger, men også geometri for trekanter og litt om brøkregning. I likhet med både babylonske, indisk og egyptiske tekster, er dette en samling av problemer, med løsning. |
|||
Blant de 246 problemene som er med i verket, inngår en figur som viser at kineserne kjente til den pytagoreiske læresetningen, med en trekant med sidelengder |
|||
3, 4 og 5.<ref name=OB/><ref name=AH87>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.87 </ref> |
|||
Figuren er gjengitt til høyre. Den vertikale teksten til venstre for figuren er som følger: |
|||
:勾股幂合以成弦幂 |
|||
:''gōu gǔ mì hé yǐ chéng xián mì'' |
|||
{{sitat|Summen av lengdene til kvadratene til høyden og basen er lik lengden til hypotenusen.|''Soluret og himmelens sirkler''{{tr}}}} |
|||
Nesten like gammelt som ''Zhoubi suanjing'', og kanskje vel så innflytelsesrikt, er verket ''[[Ni kapitler om den matematiske kunst|Chiu chang suan shu]]'' («Ni kapitler om den matematiske kunst»).<ref name=BO217/><ref name=AH87/> |
|||
Også dette er en problem-samling, med løsning på 263 matematiske problemer. I det niende og siste kapittelet omtales pytagoreiske tripler og rette trekanter.<ref>[[#FS|F. Swetz, T.I. Kao: ''Was Pythagoras Chinese? ...'']] s.?? </ref> |
|||
Et klassisk problem, som en også finner i indiske tekster, er «problemet med den brukne bambusen»:<ref name=AH87/> Et bambustre som er 10 lengder høyt, knekker. Toppen når da bakken 3 lengder fra foten av stammen. Hvor høyt oppe er |
|||
bambusen brukket? Løsningen krever bruk av Pytagoras' sats. Hvis <math>x</math> er høyden til fra foten til knekkpunktet, så er |
|||
:<math> |
|||
\begin{alignat}{2} |
|||
&(10 - x)^2 = x^2 + 3 \\ |
|||
&\Rightarrow 20x = 91 |
|||
\end{alignat} |
|||
</math> |
|||
En kommentar til ''Chiu chang suan shu'', med tittel ''[[Jiuchang suan shu]]'', ble skrevet av [[Liu Hui]] i året 263 e.Kr. Her blir det gitt et bevis{{utdyp|For hva?}} i kapittel 9.<ref>{{kilde bok |forfatter=Karine Chemla, Guo Shuchun |tittel= Les neuf chapitres. Le classique de la Chine ancienne et ses commentaires. Édition critique. |forlag=Dunod |år=2005 |side=680 |isbn=978-2100495894}}</ref> |
|||
Den pytagoreiske læresetningen var kjent i Kina under navnet ''Gōugŭ'' (勾股), «base og høyde». For en trekant med sidene 3, 4 og 5 ble læresetningen kalt ''Gōugŭ-teoremet'' (勾股定理, Gōugŭ Dìnglĭ).{{tr}} |
|||
=== Pytagoras' rolle === |
|||
{{utdypende|Pythagoras}} |
|||
[[Fil:Kapitolinischer Pythagoras adjusted.jpg|thumb|Byste av Pytagoras i [[Kapitolmuseene]] i Roma.]] |
|||
Svært lite håndfast er kjent om personen Pytagoras. Det er ikke funnet noe skriftlig verken fra ham eller fra miljøet rundt ham, og all kunnskap kommer fra senere omtale. Nøyaktig leveår for Pytagoras er ikke kjent, men det er antatt at han levde i perioden 580-475 f.Kr.<ref name=AH164>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.164 </ref> Beretninger om Pytagoras reiser til Babylonia og Egypt, fortalt av blant annet [[Jamblikos]], har i ettertiden blitt møtt med både tillit og skepsis, men det er grunn til å tro at de inneholder en kjerne av sannhet.<ref name=AH169/><ref name=AH178>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.178f </ref> Pytagoras ble leder for et filosofisk, matematisk og religiøst brorskap i [[Crotone|Kroton]], kjent som pytagoreerne. |
|||
Hvor mye kunnskap pytagoreerne hadde om sammenhengen mellom sidene i en rettvinklet trekant, er ikke kjent. Både Pytagoras og senere følgesvenner var nok fortrolige med pytagoreiske tripler, og etter tradisjonen skal kjennskapen til (3,4,5) ha kommet fra Egypt.<ref name=ESL4/> Om de hadde et bevis for sammenhengen mellom sidelengdene i en trekant, er omdiskutert. Thomas Heath gir flere bevis som ''kan'' ha vært brukt av pytagoreerne. Det er heller ikke kjent hva som ga støtet til kunnskapen om inkommensurable størrelser. Muligens kom dette fra arbeid med [[pentagram]]et, som var viktig for pytagoreerne, men det er også naturlig å anta at en likesidet trekant har vært involvert. |
|||
En tidlig kilde som tilegner teoremet til Pytagoras, skal ha vært en [[Apollodoros Arithmetikos]], og han blir sitert av flere senere kilder.<ref name=TH144/> Detaljer om Apollodoros liv er ikke kjent. Verset som blir sitert etter Apollodors er heller ikke entydig: |
|||
{{Sitat|''Da Pytagoras, som første, den berømte tegningen fant,<br /> |
|||
han brakte da som offer et guddommelig oksedyr.''|{{tr}}}} |
|||
Apollodoros sier ingenting om hvilken «berømt tegning» han viser til. Det greske ordet brukt om «tegning» kan også tolkes som «teorem».<ref name=TH144/> Fortellinger om dyreoffer som takk for kunnskap var også tidligere blitt knyttet til andre, inkludert til Thales. [[Diogenes Laertios]] (3. århundre f.Kr.) og flere andre går ut fra at verset gjelder oppdagelsen av Pytagoras' sats. Romeren [[Marcus Tullius Cicero|Cicero]] (106-43 f.Kr.) bruker fortellingen om Pytagoras og dyreofferet, uten å spesifisere hvilken geometrisk oppdagelse det gjaldt. Han er imidlertid skeptisk, fordi dyreoffer ikke var godtatt blant pytagoreerne. En annen romer, [[Vitruvius]] (ca. 80-ca.15 f.Kr.), knytter fortellingen til oppdagelsen av det pytagoreiske trippelet (3,4,5). [[Plutark]] (45-120) var kritisk til å tolke verset i tilknytning til Pytagoras' teorem. Trass denne uenigheten, var det mange som i ettertid ga Pytagoras æren for å ha oppdaget teoremet.<ref name=TH144/> Proklos i det femte århundre etter Kristus stadfester dette, uten selv å ta stilling til sannhetsinnholdet. Ifølge Proklos bør Euklid bli gitt største æren, for han var den ga bevis for teoremet. |
|||
I sitt store verk om historien til gresk matematikk, sier Thomas Heath i avsnittet om Pytagoras' teorem: |
|||
{{sitat|Though this is the proposition universally associated with the name of Pytagoras, no really thrustworthy evidence exists that it was actually discovered by him. <br/> |
|||
... <br/> |
|||
I would not go so far as to deny to Pytagoras the credit of the discovery of our proposition; nay, I like to believe that the tradition is right, and that it was really his.|Thomas Heath<ref name=TH144/>}} |
|||
I ettertiden har det vært stor uenighet om Pytagoras' rolle, og flere hypoteser er gjeldende: |
|||
* Pytagoras overtok satsen fra babylonerne. Han var kun en formidler av orientalsk kunnskap til grekerne. Dette er synet til vitenskapshistorikeren [[Walter Burkert]].<ref>{{kilde bok| forfatter=Walter Burkert |tittel=Weisheit und Wissenschaft |utgivelsessted=Nürnberg |år=1962 |side=405f, 441ff}}</ref> |
|||
* Pytagoras oppdaget og beviste satsen uavhengig av orientalsk matematikk. Dette var en vanlig oppfatning i antikken og er også synet til vitenskapshistorikeren [[Leonid Zhmud]].<ref>{{kilde bok| forfatter=Leonid Zhmud |tittel=Wissenschaft, Philosophie und Religion im frühen Pythagoreismus |utgivelsessted=Berlin |år=1997 |side=141-151, 160-163}}</ref><ref>[[#EUKLID| Euclid: ''The thirteen books of...'']] s.350-360</ref> |
|||
* Pytagoras støttet seg til orientalske kilder, men var den første som fant et bevis. Egypterne og babylonerne var primært interessert i satsens anvendelse og ikke i et generelt bevis. |
|||
* Pytagoras hadde selv få eller ingen bidrag. Andre pytagoreere kan på et senere tidspunkt ha funnet et bevis og så har dette blitt knyttet til Pytagoras. |
|||
Oppfatningen til Thomas Heath ligger kanskje et sted mellom de to siste hypotesene. |
|||
=== Euklids rolle === |
|||
{{utdypende|Evklid}} |
|||
Euklid hadde mesteparten av sitt virke i [[Alexandria]], omkring 300 f.Kr. |
|||
Beviset som Euklid bruker for Pytagoras' teorem i I.47 er antagelig hans eget.<ref name=TH378>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.378 </ref> Det betyr ikke at det ikke eksisterte eldre bevis eller at Euklid ikke kjente til disse. Euklid bygger opp ''Elementer'' svært systematisk, og beviser satsene steg for steg. Beviset for I.47 ble antagelig valgt fordi det ikke trengte bruk av formlike figurer og forhold mellom lengder. Dette emnet ble først introdusert i bok V. Pytagoras' teorem og det omvendte teoremet avslutter bok I, som høydepunkt. Så om beviset for I.47 i dag kan synes unødig komplisert, så er Euklids fortjeneste at han greidde å gjennomføre dette kun basert på innholdet i bok I. |
|||
Euklids ''Elementer'' ble antagelig skrevet som en lærebok og ikke som et forsøk på å samle all kjent geometrisk kunnskap eller presentere ny kunnskap.<ref name=TH354>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.354ff </ref> Ingenting blir nevnt om opphavet til innholdet, og heller ikke Pytagoras er nevnt. Det er antatt at store deler av innholdet i bok I, II, IV og VI var kjent for pytagoreerne.<ref name=TH201>[[#TH|T. Heath ''A history of Greek mathematics'']] (Vol. I) s.201 </ref> Euklid gjør ingen krav på originalitet, men han har antagelig laget nye bevis der dette har vært nødvendig for sammenhengen.<ref name=TH354/> Det store bidraget til Euklid var den systematiske oppbyggingen av teorien, der alt blir stringent bevist. |
|||
{{sitat|In rectangulis triangulisquadratum, quod a latere rectum angulum subtendentedescribitur, aequale est eis, quae a lateribus rectumangulum continentibus describuntur.|Euklid I.47 i latinsk versjon<ref name=ESL4>[[#ESL| E.S. Loomis: ''The Pythagorean proposition'']] s.4 </ref>}} |
|||
{{sitat|I rettvinklede trekanter er kvadratet på siden motstående til den rette vinkelen lik kvadratene på sidene som avgrenser den rette vinkelen|Euklid I.47 i norsk omsetting etter T. Heath<ref name=AH264>[[#AH| A. Holme: ''Matematikkens historie'']] (Bind 1) s.264 </ref>}} |
|||
== I kulturen == |
|||
Pytagoras' læresetning er gjennom tidene referert til eller gjengitt i en lang rekke sammenhenger: |
|||
* Et vers i «Generalmajorens sang» i musikalen ''The Pirates of Penzance'' av [[Gilbert og Sullivan]] har referansen: «About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse.» |
|||
Apollodoros sier intet om hvilken «berømte tegning» han viser til, men [[Diogenes Laertios]] (3. århundre f.Kr.) går ut fra at det gjelder Pythagoras' sats. At Pythagoras slik skulle ha ytt et storfe som offerdyr står i sterk kontrast til en rekke antikke kilder som stadfester at dyreoffer ikke var vanlig blant pytagoreerne. |
|||
* Fugleskremselet Scarecrow i [[Trollmannen fra Oz]] gir en referanse til teoremet idet han mottar eksamensbevis fra trollmannen. Han fremviser umiddelbart sin «kunnskap» ved å gjengi en radbrukket og ukorrekt versjon av teoremet: «Summen av kvadratroten på to tilfeldige sider av en likesidet trekant er lik kvadratroten av den siste siden. Oh, hurra! Jeg har vel en hjerne!» |
|||
* I en episode av ''[[Simpsons|The Simpsons]]'', etter å ha funnet [[Henry Kissinger]]s briller på toalettet i Springfield Nuclear Power Plant, tar [[Homer Simpson|Homer]] dem på og gjengir Oz Scarecrows forenklede versjon av teoremet. En mann i nærheten roper ut: «Det er en rettvinklet trekant – din idiot!» |
|||
* I talesynteseprogramvaren i [[macOS|Mac OS X]] finnes en stemme kalt Ralph, som gjengir teoremet i en eksempeltekst. |
|||
* For en ''Past Master'' bruker [[frimureri|frimuerere]]et symbol som er et diagram Euklid brukte i sitt bevis av teoremet. |
|||
* I [[Neal Stephenson]]s spekulative fiction ''Anathem'' er Pytagoras' teorem gjengitt som ''the Adrakhonic theorem''. Et geometrisk bevis er gjengitt på et romskip, for å vise eiernes kunnskap om matematikk. |
|||
* I den engelske versjonen av den syttende boken om [[Asterix]], ''The Mansions of the Gods'', benytter [[Julius Cæsar]] seg av tjenesten til arkitekten ''Squareonthehypotenus'' (''Kvadratetpåhypotenusen''). |
|||
* I 2000 utga Uganda en mynt med form som en rett trekant. Myntens bakside har en illustrasjon av Pytagoras og Pytagoras' teorem, sammen med teksten «Pythagoras Millennium».<ref>{{Kilde www| url=http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm| tittel=Le Saviez-vous ?| dødlenke=ja| arkivurl=https://web.archive.org/web/20090921060307/http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm| arkivdato=2009-09-21}}</ref> |
|||
* Hellas, Japan, San Marino, Sierra Leone og Surinam er alle land som har gitt ut frimerker med motiver av Pytagoras og Pytagoras' teorem.<ref>{{Kilde www| url=http://members.tripod.com/jeff560/index.html| tittel=Images of mathematicians on postage stamps| forfatter=Miller, Jeff| dato=3. august 2007| besøksdato=6. august 2007}}</ref> |
|||
Historien om |
Historien om dyreofferet til Pytagoras har inspirert dikteren [[Adelbert von Chamisso]] til en [[sonett]], ''Vom pythagoreischen Lehrsatz'', der første vers lyder:{{tr}} |
||
{{Sitat|Die Wahrheit, sie besteht in Ewigkeit, <br /> |
{{Sitat|Die Wahrheit, sie besteht in Ewigkeit, <br /> |
||
| Linje 397: | Linje 646: | ||
{{Sitat|Evighet er Sannhetens byggekloss, <br /> |
{{Sitat|Evighet er Sannhetens byggekloss, <br /> |
||
At verden så lyset, er hva det krevde; <br /> |
At verden så lyset, er hva det krevde; <br /> |
||
Den læresetningen |
Den læresetningen Pytagoras ga oss <br /> |
||
Gjelder like mye |
Gjelder like mye i dag som da han levde.}} |
||
== |
== Referanser == |
||
<references/> |
|||
Pythagoras' læresetning er gjennom tidene referert til eller gjengitt i en lang rekke sammenhenger: |
|||
== Litteratur == |
|||
* Et vers i ''Generalmajorens sang'' i musikalen The Pirates of Penzance av [[Gilbert og Sullivan]] har en klar referanse: ''About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse''. |
|||
* Scarecrow ([[fugleskremsel]]et) i [[Trollmannen fra Oz]] gir en spesifikk referanse til teoremet idet han mottar sitt eksamensbevis fra trollmannen. Han fremviser umiddelbart sin «kunnskap» ved å gjengi en radbrukket og ukorrekt versjon av teoremet: ''Summen av kvadratroten på to tilfeldige sider av en likesidet trekant er lik kvadratroten av den siste siden. Oh, hurra! Jeg har vel en hjerne!'' |
|||
* I en episode av ''[[The Simpsons]]'', etter å ha funnet [[Henry Kissinger]]s briller på toalettet i Springfield Nuclear Power Plant, tar [[Homer Simpson|Homer]] dem på og gjengir Oz Scarecrow's forenklede versjon av teoremet. En mann i nærheten roper ut: ''Det er en rettvinklet trekant – din idiot!''. |
|||
* I talesynteseprogramvaren i [[Mac OS X]] finnes en stemme kalt Ralph som gjengir teoremet i en eksempeltekst. |
|||
* Innen [[Frimureri]] brukes et symbol for en ''Past Master'' som er et diagram Euklid brukt i sitt bevis av teoremet. |
|||
* I [[Neal Stephenson]]s spekulative fiction ''Anathem'' er Pythagoras' teorem gjengitt som ''the Adrakhonic theorem''. Et geometrisk bevis er gjengitt på et romskip for å demonstrere deres kunnskaper om matematikk. |
|||
* I den engelske versjonen av den 17. boken om [[Asterix]]: ''The Mansions of the Gods'', benytter [[Julius Cæsar]] seg av tjenesten til arkitekten ''Squareonthehypotenus''. (''Kvadratetpåhypotenusen'') |
|||
* I 2000 utga [[Uganda]] en mynt med form som et rett triangel. Myntens bakside har et bilde av Pythagoras og Pythagoras' teorem sammen med teksten: ''Pythagoras Millennium''.<ref> |
|||
{{Kilde www |
|||
| url=http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm |
|||
| tittel=Le Saviez-vous ? |
|||
| dødlenke=ja |
|||
| arkivurl=https://web.archive.org/web/20090921060307/http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm |
|||
| arkivdato=2009-09-21 |
|||
}} |
|||
</ref> |
|||
* [[Hellas]], [[Japan]], [[San Marino]], [[Sierra Leone]], og [[Surinam]] har gitt ut [[frimerke]]r med motiver av Pythagoras og Pythagoras' teorem.<ref> |
|||
{{Kilde www |
|||
| url=http://members.tripod.com/jeff560/index.html |
|||
| tittel=Images of Mathematicians on Postage Stamps |
|||
| forfatter=Miller, Jeff |
|||
| dato=3. august 2007 |
|||
| besøksdato=6. august 2007}} |
|||
</ref> |
|||
'''På norsk''': |
|||
== Noter == |
|||
<references> |
|||
*{{Kilde bok |
|||
<ref name="Boyer207"> |
|||
| ref=AH |
|||
Boyer s.207 sitat: «we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. However all of these triads are easily derived from the old Babylonian rule; hence, Mesopotamian influence in the ''Sulvasutras'' is not unlikely. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides, but this form of the Pythagorean theorem also may have been derived from Mesopotamia. [...] So conjectural are the origin and period of the ''Sulbasutras'' that we cannot tell whether or not the rules are related to early Egyptian surveying or to the later Greek problem of altar doubling. They are variously dated within an interval of almost a thousand years stretching from the eighth century B.C. to the second century of our era.» |
|||
| forfatter= Holme, Audun |
|||
</ref> |
|||
| utgivelsesår=2008 |
|||
| tittel=Matematikkens historie |
|||
| utgivelsessted=Bergen |
|||
| forlag=Fagbokforlaget |
|||
| bind=1 |
|||
| isbn=978-82-450-0697-1}} |
|||
'''På engelsk:''' |
|||
</references> |
|||
*{{Kilde bok |
|||
== Litteratur == |
|||
| ref=BOYER |
|||
| forfatter= Boyer, Carl B. |
|||
| utgivelsesår=1968 |
|||
| tittel=A history of mathematics |
|||
| utgivelsessted= Princeton, USA |
|||
| forlag= John Wiley & Sons, Inc |
|||
| isbn= 0-691-02391-3 }} |
|||
* {{kilde bok |
|||
| ref=EUKLID |
|||
| forfatter=Euclid |
|||
| tittel=The thirteen books of the Elements. Translated with an introduction and commentary by Sir Thomas L. Heath |
|||
| bind=I, II og III |
|||
| forlag=Dover |
|||
| isbn=978-0-486-60088-8 |
|||
| utgivelsesår=1956}} |
|||
*{{Kilde bok |
|||
| ref=TH |
|||
| forfatter= Heath, Thomas |
|||
| utgivelsesår=1981 |
|||
| tittel=A history of Greek mathematics |
|||
| bind=I og II |
|||
| utgivelsessted=New York |
|||
| forlag=Dover Publications |
|||
| isbn=0-486-24073-8 }} |
|||
*{{kilde bok |
|||
| ref=ESL |
|||
| forfatter=Loomis, Elisha Scott |
|||
| tittel=The Pythagorean proposition |
|||
| utgivelsessted=Washington, D.C |
|||
| forlag=The National Council of Teachers of Mathematics |
|||
| utgivelsesår=1968 |
|||
| isbn=978-0873530361 |
|||
| url=https://files.eric.ed.gov/fulltext/ED037335.pdf }} |
|||
*{{kilde bok |
|||
| forfatter=Maor, Eli |
|||
|tittel=The Pythagorean theorem: A 4,000-Year History |
|||
|utgivelsessted==Princeton, New Jersey |
|||
|forlag=Princeton University Press |
|||
|år=2007 |
|||
|isbn=978-0-691-12526-8}} |
|||
*{{kilde bok |
|||
| forfatter=Stillwell, John |
|||
|tittel=Mathematics and its history |
|||
|forlag=Springer-Verlag |
|||
|år=1989 |
|||
|isbn=3-540-96981-0}} |
|||
*{{kilde bok |
|||
|ref=FS |
|||
|forfatter=Swetz, Frank, Kao, T. I. |
|||
|tittel=Was Pythagoras Chinese? An examination of right triangle theory in ancient China |
|||
|forlag=Pennsylvania State University Press |
|||
|år=1977}} |
|||
*{{kilde bok |
|||
| ref=WAE |
|||
| forfatter=van der Waerden, B.L. |
|||
|tittel=Geometry and algebra in ancient civilizations |
|||
|forlag=Springer |
|||
|år=1983 |
|||
|isbn= 978-0387121598}} |
|||
'''På engelsk:''' |
|||
{| |
|||
|valign="top"| |
|||
* Bell, John L., ''[http://publish.uwo.ca/~jbell/ The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development]'', Kluwer, 1999. ISBN 0-7923-5972-0. |
|||
* {{Kilde bok |
|||
| forfatter=Boyer, Carl B. |
|||
| tittel=A History of Mathematics, 2nd Edition |
|||
| utgivelsesår=1991 |
|||
| kapittel=China and India |
|||
| isbn=9780471543978 |
|||
}} |
|||
* Eli Maor: ''The Pythagorean Theorem: A 4,000-year History''. Princeton University Press 2007, ISBN 0-691-12526-0 |
|||
* Euclid, ''The Elements'', Translated with an introduction and commentary by Sir Thomas L. Heath, Dover, (3 vols.), 2nd edition, 1956. |
|||
* Hardy, Michael, "Pythagoras Made Difficult". ''Mathematical Intelligencer'', '''10''' (3), p. 31, 1988. |
|||
* Heath, Sir Thomas, ''A History of Greek Mathematics'' (2 Vols.), Clarendon Press, Oxford (1921), Dover Publications, Inc. (1981), ISBN 0-486-24073-8. |
|||
* Loomis, Elisha Scott, ''The Pythagorean proposition''. 2nd edition, Washington, D.C : The National Council of Teachers of Mathematics, 1968. ISBN 978-0873530361. |
|||
* Maor, Eli, ''The Pythagorean Theorem: A 4,000-Year History''. Princeton, New Jersey: Princeton University Press, 2007, ISBN 978-0-691-12526-8. |
|||
* Stillwell, John, ''Mathematics and Its History'', Springer-Verlag, 1989. ISBN 0-387-96981-0 and ISBN 3-540-96981-0. |
|||
* Swetz, Frank, Kao, T. I., ''Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China'', Pennsylvania State University Press. 1977. |
|||
* van der Waerden, B.L., ''Geometry and Algebra in Ancient Civilizations'', Springer, 1983. |
|||
|width="50"| |
|||
|valign="top"| |
|||
'''På tysk:''' |
'''På tysk:''' |
||
* Colerus, Egmont : ''Vom Einmaleins zum Integral. Mathematik für Jedermann.'' Rowohlt, Reinbek 1982. ISBN 3-499-16692-5 |
|||
*{{kilde bok| forfatter=Fraedrich, Anna M. |tittel=Die Satzgruppe des Pythagoras |forlag=Spektrum Akademischer Verlag |utgivelsessted=Heidelberg |år=1994 |isbn=3-86025-669-6}} |
|||
* Dewdney, Alexander K. : ''Reise in das Innere der Mathematik.'' Birkhäuser, Berlin 2000. ISBN 3-7643-6189-1 |
|||
*{{kilde bok |ref=HG |forfatter=Gericke, Helmuth |tittel=Mathematik in Antike und Orient |forlag=Springer |utgivelsessted=Berlin |isbn= 978-3-642-68630-6 |år=1984}} |
|||
* Fraedrich, Anna M. : ''Die Satzgruppe des Pythagoras.'' Spektrum Akademischer Verlag, Heidelberg 1994. ISBN 3-86025-669-6 |
|||
*{{kilde bok |ref=KV |forfatter=Vogel, Kurt |tittel=Vorgriechische Mathematik |forlag=Hermann Schroedel |bind=Teil II: Die Mathematik der Babylonier |utgivelsessted=Hannover |år=1959}} |
|||
* Resnikoff,H.L.; Wells Jr.,R.O.: ''Mathematik im Wandel der Kulturen.'' Vieweg, Braunschweig/Wiesbaden 1983. ISBN 3-528-03578-1 |
|||
* Schupp, Hans : ''Elementargeometrie.'' UTB, Stuttgart 1977. ISBN 3-506-99189-2 |
|||
* Singh, Simon : ''Fermats letzter Satz.'' dtv, München 2000. ISBN 3-423-33052-X |
|||
* Tietze, Heinrich : ''Mathematische Probleme. Gelöste und ungelöste mathematische Probleme aus alter und neuer Zeit. Vierzehn Vorlesungen für Laien und Freunde der Mathematik.'' C.H. Beck, München 1990. ISBN 3-406-02535-8 |
|||
|} |
|||
== Eksterne lenker == |
== Eksterne lenker == |
||
* {{Offisielle lenker}} |
* {{Offisielle lenker}} |
||
* |
* {{kilde www|url=http://www.cut-the-knot.org/pythagoras/index.shtml |tittel=Pythagorean Theorem |utgiver=Cut the Knot |språk=en |besøksdato=2021-03-15 |kommentar=Mer enn 70 bevis}} |
||
* {{kilde www|url=http://www-groups.dcs.st-and.ac.uk/~history/PrintHT/Babylonian_Pythagoras.html |tittel=Pythagoras's Theorem in Babylonian Mathematics |utgiver=MacTutor |språk=en |besøksdato=2021-03-15 |kommentar=}} |
|||
* Interaktive lenker: |
|||
* {{kilde www|url=http://mathworld.wolfram.com/PythagoreanTheorem.html |tittel= Pythagorean Theorem |utgiver=Wolfram MathWorld |språk=en |besøksdato=2021-03-15 |kommentar=}} |
|||
** [http://www.sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html Interaktivt bevis av Det pytagoreiske teorem], i [[Java (programmeringsspråk)|Java]] |
|||
* {{kilde www|url=https://mathcs.clarku.edu/~djoyce/java/elements/toc.html |tittel=Euclid's Elements|utgiver = Clark University, USA| språk=en |besøksdato=2021-03-15 |kommentar=}} |
|||
** [http://www.cut-the-knot.org/pythagoras/Perigal.shtml Enda et interaktivt bevis], i [[Java (programmeringsspråk)|Java]] |
|||
** [http://www.mathopenref.com/pythagorastheorem.html Det pytagoreiske teorem] med interaktiv animasjon |
|||
** [https://web.archive.org/web/20090530072020/http://math.ucr.edu/~jdp/Relativity/Pythagorus.html Animert, ikke-algebraisk fremvisning] av Det pytagoreiske teorem |
|||
** [https://web.archive.org/web/20100103070358/http://www.ies.co.jp/math/java/geo/pythagoras.html Animasjon] |
|||
* [http://www.gogeometry.com/pythagoras/right_triangle_formulas_facts.htm Det pytagoreiske teorem og formler for rette trekanter] {{Språkikon|en|engelsk}} |
|||
* [http://www-groups.dcs.st-and.ac.uk/~history/PrintHT/Babylonian_Pythagoras.html Historisk emne: Pythagoras' teorem i babylonsk matematikk] {{Språkikon|en|engelsk}} |
|||
* [http://mathworld.wolfram.com/PythagoreanTheorem.html Eric Weisstein: PythagoreanTheorem i MathWorld] |
|||
* [https://web.archive.org/web/20090913033515/http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/ Flere animerte bevis av Pythagorasteoremet] {{Språkikon|de|tysk}} |
|||
* [https://web.archive.org/web/20100126151357/http://www.didmath.ewf.uni-erlangen.de/Verschie/Gut_Ref/Pythago/Pythagoras.html Bevis av Pythagorasteoremet] {{Språkikon|de|tysk}} |
|||
* [http://www.asamnet.de/~sigwarts/facharbeit/titel.htm Interaktivt læreprogram med beviser, oppgaver og flere lenker] |
|||
* R. Moosbrugger: ''[https://web.archive.org/web/20111114002956/http://www.geomatik.ch/fileadmin/download/2006/Fach/FA_1_2006_6.pdf Schnurvermessung: einfältig – einfach]''. |
|||
{{Matematikk}} |
|||
{{ |
{{Utmerket}} |
||
{{Autoritetsdata}} |
{{Autoritetsdata}} |
||
{{Utmerket}} |
|||
[[Kategori:Euklidsk plangeometri]] |
[[Kategori:Euklidsk plangeometri]] |
||
Sideversjonen fra 17. mar. 2021 kl. 13:52

Pytagoras' læresetning eller den pytagoreiske læresetning er i euklidsk geometri et fundamentalt teorem om sammenhengen mellom sidelengdene i en rettvinklet trekant:
- «I en rettvinklet trekant er summen av kvadratene på katetene lik kvadratet på hypotenusen.»
De to katetene er de korteste sidene i trekanten, og hypotenusen er den lengste. Den rette vinkelen er motstående til hypotenusen. Kaller man lengdene av katetene henholdsvis og samt lengden av hypotenusen for , så kan læresetningen uttrykkes som en ligning, ofte kalt Pytagoras ligning:[1]
- .
Heltall som oppfyller Pytagoras' læresetning kalles pytagoreiske tripler. Et velkjent trippel er (3,4,5). Dersom sidelengdene i en trekant danner et pytagoreiske trippel, så er trekanten rettvinklet.
Det eksisterer mange generaliseringer av Pytagoras' teorem. En generalisering til en vilkårlig trekant kalles den utvidede pytagoreiske læresetning eller cosinussetningen.
Det historiske opphavet til teoremet er bare mangelfullt kjent og har vært gjenstand for mye diskusjon. Navnet har teoremet fått fordi mange tradisjonelt har knyttet læresetningen til den greske matematikeren Pytagoras, som levde omkring 500 f.Kr. Det eksisterer imidlertid ikke gode indikasjoner eller bevis for at han eller noen av hans følgesvenner skal ha vært opphavsmann til teoremet. Pytagoreiske tripler og andre former for teoremet har vært kjent i babylonsk, egyptisk, kinesisk og indisk matematikk lenge før pytagoreerne. Kanskje har læresetningen blitt oppdaget flere steder og til flere tider uavhengig av hverandre. Det eldste deduktive bevis vi kjenner, er fra Euklids Elementer, skrevet omkring 300 f.Kr. I dag eksisterer det en lang rekke alternative bevis for teoremet.
Bevis


Pytagoras' læresetning antas å være et av de teoremene i matematikk som er bevist på flest alternative måter. Boken Pythagorean Proposition av Elisha Scott Loomis inneholder hele 370 bevis.[2] I boken er 109 bevis karakterisert som algebraiske og 255 som geometriske. De resterende seks er basert på vektorregning eller dynamiske argument. Et geometrisk bevis bygger i følge Loomis på sammenligning av arealet til de tre kvadratene konstruert fra sidelengdene, mens et aritmetisk er basert på lineære relasjoner mellom sidelengder eller areal, for eksempel ved bruk av formlike trekanter. Denne inndelingen er kanskje ikke entydig, og mange bevis har innslag av både geometri og algebra.
Euklids bevis
I Euklids Elementer, teorem 47 i bok I, finner man det eldste kjente beviset for Pytagoras' teorem.[3][4] Det er vanlig å referere til Euklids bøker med romertall for bindet og et vanlig tall for den gjeldende satsen, slik at Pytagoras' teorem er I.47. Beviset for I.47 er basert på en sammenligning av areal.
La , og være hjørnene i en rettvinklet trekant, med den rette vinkel ved som vist på figuren. Til hver side i trekanten er det tegnet et kvadrat. En normal fra hjørnet til hypotenusen deler kvadratet på hypotenusen i to rektangler, på figure vist i blått og rosa. Euklid beviste setningen ved å vise at arealet til hver av de to minste kvadratene er lik arealet av ett av rektanglene, vist med fargene i figuren. Arealsummen av de to minste kvadratene er dermed lik arealet til det største kvadratet.
Beviset bygger på flere hjelpesetninger, som Euklid viser tidligere i bok I. Disse vil bli brukt videre, uten bevis her.
- Hvis to trekanter er slik at to sider i den ene er lik tilsvarende to sider i den andre, og den mellomliggende vinkel er lik i begge, så er trekantene kongruente.
- Arealet av en gitt trekant er lik halvparten av arealet i et vilkårlig parallellogram med samme grunnlinje og høyde.
- Arealet av et rektangel er lik produktet av to tilstøtende sider.
- Arealet av et kvadrat er lik produktet av to sider.
Beviset er som følger:
- La være en rettvinklet trekant, med den rette vinkelen gitt ved .
- På hver av sidene , og tegnes kvadrater, henholdsvis , og .
- Fra trekkes en linje parallell med og . Den krysser og i rett vinkel ved henholdsvis og .
- Forbind og . Derved dannes trekantene og .
- Vinklene og er begge rette. Punktene , og ligger derfor på samme linje. Tilsvarende ligger , og på en rett linje.
- Vinklene og er begge rette. Dermed er lik , siden begge er summen av en rett vinkel og den felles .
- Siden og er tilsvarende like med og , må trekanten være kongruent med trekanten .
- Ved bruk av hjelpesetning nr.2 må rektangelet være dobbelt så stort som trekanten .
- Ved bruk av hjelpesetning nr.2 må rektangelet være dobbelt så stort som trekanten .
- Dermed må rektangelet ha samme areal som kvadratet , det vil si at .
- Tilsvarende kan det vises at rektangelet må ha samme areal som kvadratet , det vil si at .
- Ved å addere disse to resultatene: .
- Siden , så er .
- Dermed er , siden er et kvadrat.
Beviset har tidligere vært pensum i norsk realskole.[trenger referanse] Det finnes enklere bevis, men gjennomgang av fremgangsmåten kan være en egnet øvelse i matematisk tenkning.
Figuren til Euklids bevis, med hjelpelinjer til alle fire kvadrater, er berømt. Den er blitt beskrevet som en «vindmølle», en «brudestol» og en «påfugl-hale».[3] Også navnet pons asinorum er blitt brukt om figuren.[5] Dette latinske utrrykket betyr «eselbroen» eller «idiotbroen», og uttrykket knyttes vanligvis til en annen Euklid-figur, brukt i forbindelse med Elementer I.5.[6]
Bevis ved bruk av formlike trekanter

Mange av bevisene for Pytagoras' setning er basert på forhold mellom sidelengder i to formlike trekanter. Elisha Scott Loomis omtaler dette som det korteste av alle Pytagoras-bevisene og kaller det også for «Legendre-beviset».[7] En lærebok i geometri fra 1858, basert på arbeid av Adrien-Marie Legendre, gjengir beviset. Thomas Heath foreslår dette som ett alternativ for et bevis som kan ha vært brukt av pytagoreerne.[8]
La være en rettvinklet trekant. Den rette vinkelen er ved , slik figuren viser. Høyden fra hjørnet treffer siden i fotpunktet . Trekanten er formlik med trekanten , da begge er rettvinklede og vinkelen ved er felles. Tilsvarende er trekanten formlik med . Tilsammen resulterer dette i følgende forhold mellom sidelengder:
Dette kan skrives som
Summasjon av de to uttrykkene gir
Garfields bevis

James Garfield er opphavsmann for det følgende beviset.[9][10] Han var jurist og medlem av den amerikanske Kongressen, og han oppdaget beviset i 1876 som følge av en matematisk diskusjon med andre kongressmedlemmer. Garfield ble president i USA i 1881, men han ble skutt og drept etter bare fire måneder i embedet.
Arealet av et generelt trapes med høyde og lengder av de to parallelle sidene og er gitt ved
Da er arealet av trapeset vist i figuren:
Trekant 1 og 2 er identiske, med areal
- .
Trekant 3 er rettvinklelt, og arealet er lik halvparten av kvadratet på hypotenusen:
Et alternativt uttrykk for arealet til trapeset finner en ved å summere arealene til de tre trekantene:
En sammenstillingen av de to uttrykkene for trapesarealet gir
Bevis ved reorganisering

Det eksisterer flere bevis basert på å reorganisere areal. Et eksempel er vist i figuren til venstre. De to store kvadratene i figuren er like store, begge med sidelengde . De to kvadratene skiller seg kun ved den innvendige plasseringen av de fire trekantene. Arealet av de hvite områdene i de to store kvadratene må derfor være like, og dette gir Pytagoras' setning.
Thomas Heath omtaler dette beviset og et forslag fra de to matematikerne Carl Anton Bretschneider og Hermann Hankel om at dette kan ha vært kjent av pytagoreerne.[8] Heath vil ikke avvise en slik teori, men mener selv at det er mer sannsynlig at pytagoreerne kjente beviset basert på formlike trekanter.
Algebraisk bevis
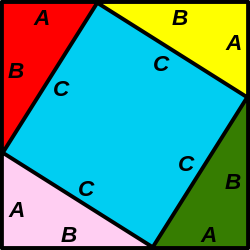
Et algebraisk bevis kan gjennomføres ved å betrakte fire identiske trekanter plassert i hjørnene til et større kvadrat.[11] Beviset er gjengitt av den indiske matematikeren Bhaskara, som levde på 1200-tallet.
Sidelengdene i trekantene er , og , og det store kvadratet har sidelengde .
Arealet av hver av de fire trekantene er gitt ved:
I hver trekant er motstående vinkel til -siden og -siden komplementvinkler. Også det blå området er derfor et kvadrat, med areal lik . Arealet til det store kvadratet med sidelengde er gitt ved
Alternativt kan dette uttrykkes som arealsummen for de fire trekantene og det blå kvadratet:
En sammenstilling av de to uttrykkene for gir Pytagoras' teorem.
Det omvendte teoremet
Euklid viste i teorem I.48 at også det omvendte Pytagoras' teorem er gyldig, der en bytter forutsetning og konklusjon:[12]
- «For tre vilkårlige, positive tall a, b og c der a2 + b2 = c2, finnes det en rettvinklet trekant med sider a, b og c. Den rette vinkelen er mellom sidene med lengde a og b.»
Teoremet kan bevises som følger:
La være en trekant med sidelengder , og . Anta også at . Konstruerer en ny rettvinklet trekant , med den rette vinkelen mellom sider med lengde og . Fra Pytagoras' setning følger det at hypotenusen i trekant har lengde . Trekantene og har tre like sider og er derfor kongruente. Følgelig har de også like vinkler. I trekant må derfor vinkelen mellom sidelengdene and være en rett vinkel.
Pytagoreiske tripler
Et pytagoreisk trippel består av tre positive heltall , , og , slik at .[13] En vanlig skrivemåte for et slikt trippel er . Et pytagoreiske trippel representerer sidelengdene i en rettvinklet trekant, når alle tre lengdene har heltallsverdier. Et velkjent eksempel er (3,4,5).
Dersom er et pytagoreisk trippel, så vil også være det, for et vilkårlig heltall . Dersom de tre tallene , , og ikke har noen felles faktor, så kalles de tre tallene for et primitivt trippel.[1] Tallene er da relativt primiske. Mens (3, 4, 5) er et primitivt trippel, er (6, 8, 10) et trippel med en felles faktor 2.
Pytagoreiske tripler kan brukes til å konstruere rette vinkler og til å kontrollere om en gitt vinkel er rett. Et hendig trippel er (60,80,100), et ikke-primitivt trippel som kan dannes ved å multiplisere tallene i (3,4,5) med 20. En vinkel i et innvendig hjørne i et rom kan kontrolleres ved å avsette henholdsvis 60 cm langs den ene veggen, 80 cm langs den andre. Om nå en meter-lengde passer mellom merkene, så er vinkelen rett.
En enkel omforming av ligningen for et pytagoreisk trippel gir
Å finne pytagoreisk tripler svarer altså til å finne et punkt på en enhetssirkel, der koordinatene er gitt ved to rasjonale tall.[14] Formler for å konstruere pytagoreiske tripler har vært kjent i svært lang tid. De to følgende formlene skal være funnet av henholdsvis Pytagoras og Platon:[15]
I bok X gir Euklid et enda videre uttrykk for pytagoreiske tripler. Aæren for det generelle uttrykket for alle primitive pytagoreiske tripler er gitt til Diofant, som levde omkring 200 år etter Kristus:[16]
Her er og to vilkårlige, positive heltall som ikke begge er oddetall. Dessuten er , og de to tallene skal ikke ha noen felles faktor.
Primitive pytagoreiske tripler opp til 100
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).
Konsekvenser og bruk av læresetningen
Inkommensurable lengder og irrasjonale tall
En konsekvens av Pytagoras' teorem er at det er mulig å konstruere inkommensurable lengder, det vil si lengder med et forhold lik et irrasjonalt tall. Et enkelt eksempel er gitt ved rettvinklet trekant der begge katetene har lengde 1. Pytagoras' setning gir at hypotenusen i en slik trekant har lengde lik kvadratroten av 2. At dette tallet er et irrasjonalt tall, kan vises ved et enkelt algebraisk bevis, se Kvadratroten av 2.
For greske matematikere var en irrasjonell størrelse definert som et forhold mellom lengder og ikke som et tall. Det skulle gå lang tid før en forståelse av irrasjonale tall skulle bli etablert. Eksistensen av inkommensurable lengder har opphav hos pytagoreerne, men det er ikke kjent nøyaktig når og hvordan kjennskap til slike størrelser ble etablert.[17] Historikeren Proklos, som levde i det femte århundre etter Kristus, gir æren til Pytagoras selv, men ifølge Thomas Heath er det mest sannsynlig at kunnskapen oppstod en god stund etter at Pytagoras var død. En av flere alternative historier om pytagoreeren Hippasos et at han ble druknet, etter å ha røpet kunnskapen om inkommensurable størrelser.[18] Euklid bruker bok X til å diskutere inkommensurable lengder og areal.[19]
Distanse i euklidske rom
Metrikken eller avstandsmålet i euklidsk geometri er basert på Pytagoras' teorem. Hvis og er kartesiske koordinater til to punkt i planet, så er avstanden mellom disse gitt ved
Dette avstandsmålen kalles euklidsk avstand eller euklidsk metrikk.
I et generelt euklidsk n-dimensjonalt rom er avstanden mellom to vektorer og definert ved
Bruk i kompleks analyse

Et vilkårlig komplekst tall kan skrives på formen
Absoluttverdien eller modulus til dette tallet er definert ved[20]
Sammenhengen mellom de tre størreslene , og er gitt ved Pytagoras' ligning:
Absoluttveriden er alltid definert positiv, selv om og kan ha både positive og negative verdier. Geometrisk er avstanden fra origo til i det komplekse planet.
Avstanden mellom to komplekse tall og kan defineres ved
Denne avstanden og de to gitte tallene er igjen relatert ved en ligning tilsvarende Pytagoras' ligning:
Den pytagoreiske trigonometriske identiteten

For en rettvinklet trekant, som vist nederst i figuren til høyre, kan de trigonometriske funksjonene sinus og cosinus defineres ved
Ved å bruke Pythagoras' teorem, følger det fra disse definisjonene at
Denne grunnleggende identiteten blir kalt enhetsformelen og noen ganger også den pytagoreiske trigonometriske identiteten.[trenger referanse] For to formlike trekanter er forholdet mellom samsvarende sidelengder det samme, og dette vil også gjelde for de to trekantene i figuren. Den øverste rettvinklet trekanten har hypotenusen med lengde 1, og katetene har lengde og .
Generaliseringer
Cosinussetningen
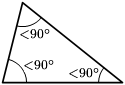
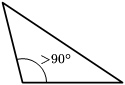
Pytagoras' teorem er et spesialtilfelle av et mer generelt teorem om forholdet mellom sidelengder i en vilkårlig trekant, kjent som cosinussetningen eller den utvidede pytagoreiske læresetning.[21][22] For en vilkårlig trekant med sidelengder , og er
- .
Her er vinkelen mellom sidene med lengde og . For lik 90 grader er , og ligningen reduserer seg til den vanlige pytagoreiske ligningen.
Cosinussetningen gir en enkel metode for å bestemme om en trekant er rett, spissvinklet eller stumpvinklet, Siden cosinus-funksjonen er positiv for en spiss vinkel, men negativ for en stump vinkel, så gjelder følgende:
- hvis og bare hvis trekanten er rettvinklet.
- hvis og bare hvis trekanten er spissvinklet.
- hvis og bare hvis trekanten er stumpvinklet.
Her er forutsatt at er den lengste siden. En vanlig notasjon er å la vinklene i trekanten være , slik at er motstående til sidelengden og motstående til sidelengden . Forholdene over kan da også uttrykkes slik:
- I en spissvinklet trekant er og .
- I en stumpvinklet trekant er og .
Edsger Dijkstra har samlet disse resultatene ved hjelp av fortegnsfunkjonen:[23]
Parallellogramloven

Parallellogramloven er en generalisering av Pytagoras' sats til et vilkårlig parallellogram, tilskrevet Apollonios fra Perge.[24]
For et rektangel er de to diagonalene like lange: , og parallellogramloven reduserer seg til Pytagoras’ læresetning.
Formlike figurer
Pytagoras' læresetning kan tolkes som en relasjon mellom arealet til kvadrater på sidekantene. Ved å multiplisere alle tre leddene i Pytagoras' ligning med , ser en umiddelbart at samme relasjon også gjelder for arealene til halvsirkler med diameter langs sidekantene. Dette resultatet er referert uten bevis av Hippokrates fra Khíos, som levde i det femte århundre før Kristus.[25] Euklid viste i bok VI av Elementer et bevis for a resultatet gjelder for vilkårlige formlike konvekse polygon.[25] I ettertid er det vist at resultatet er gyldig for vilkårlige formlike figurer, også figurer der sider er definerte ved kurver:[trenger referanse]
- «Hvis en reiser formlike figurer på sidene av et rett trekant, så er summen av arealene på de to minste sidene lik arealet av figuren på den største siden.»
De tre sidelengdene i den rette trekanten er lik sidelengder i de tilstøtende figurene, slik at disse må være formlike i forholdet . Den grunnleggende idéen bak generaliseringen er at i formlike figurer er forholdet mellom arealet og kvadratet av en vilkårlig karakteristisk lengde det samme:
 |
 |
Pappos arealteorem
Pappos (3-4. århundre) gir et arealteorem han selv kaller en utviding av Euklid I.47.[26] Dersom en på to sider i en vilkårlig trekant tegner to vilkårlige parallellogram, så kan en konstruere et parallellogram på den tredje siden, slik at arealet av dette er lik summen av arealene til de to første.
 |
Romgeometri

En lengde i det tredimensjonale rommet kan defineres ved gjentatt bruk av Pytagoras' setning. I figuren til høyre kan en finne lengden av linjestykket ved å bruke den rettvinklede trekanten :
Kateten i denne er gitt ved å bruke Pytagoras' sats på trekanten :
Kombinasjon av disse to ligningene gir
Resultatet er det tredimensjonale uttrykket for lengden av en vektor , basert på komponentene. Vektoren svarer til diagonalen
de Guas teorem
I tre romdimensjoner er de Guas teorem en generalisering av Pytagoras' læresetning til et tetraeder:[27]
- «Hvis et tetraeder har et rettvinklet hjørne, så er kvadratet av arealet på den motstående side til den rette vinkel lik summen av kvadratene av arealene på de tre andre sidene.»
Et rettvinklet hjørne er som hjørnet i en kube. Teoremet er navngitt etter Jean Paul de Gua de Malves (1713-1785).
Indreproduktrom
Pytagoras' sats kan generaliseres til et vilkårlig indreproduktrom, som igjen er en generalisering av det euklidske rommet i to og tre dimensjoner.[28] Et indreproduktrom kan ha både endelig og uendelig dimensjon. Elementene i et indreproduktrom, vektorene, kan for eksempel være funksjoner. I et indreproduktrom kan en definere lengden av elementer, avstanden mellom to elementer og også vinkelen mellom to elementer.
Indreproduktet mellom to elementer og kan betegnes som , og dette generaliserer det vanlige skalarproduktet mellom to endelig-dimensjonale vektorer. To vektorer står ortogonalt på hverandre dersom indreproduktet mellom dem er lik null. Lengden av en vektor er definert ved normen:
I et indreproduktrom sier Pytagoras' teorem at for to ortogonale vektorer og gjelder at
Vektorene og spiller samme rolle som katetene i en rettvinklet trekant, med hypotenusen gitt som vektorsummen . Teoremet følger av egenskaper til indreproduktet:
Ligningen kan generaliseres til et vilkårlig endelig antall parvis ortogonale vektorer:
Også parallellogramloven kan generaliseres til et vilkårlig indreproduktrom, da med formen
Differensialgeometri
I differensialgeometri blir det for det tredimensjonale euklidske rommet definert en infinitesimal lengde ved[29]
- .
Dette svarer til bruk at Pytagoras' setning for en infinitesimal avstand mellom to punkt. For en glatt parametrisk kurve gitt på formen
brukes dette til å definere buelengden av kurven:
Ikke-euklidsk geometri
Pytagoras' setning er basert på aksiomer i euklidsk geometri, og den euklidske formen er ikke gyldig i ikke-euklidsk geometri. I sfærisk geometri vil for eksempel alle tre sidene i en rettvinklet trekant som begrenser en oktant i en enhetskule, ha sidelengder . Dette bryter opplagt med Pytagoras' ligning.
For ikke-euklidsk geometri kan en utlede alternative former for Pytagoras' teorem. I sfærisk geometri gjelder det at for enhver rettvinklet sfærisk trekant, på en kule med radius , kan Pytagoras' teorem skrives som:
Når radien går mot uendelig, vil kuleflaten nærme seg en plan flate. Tilsvarende vil den sfæriske formen på Pytagoras' teorem gå mot den euklidske formen. Dette kan vises ved å utvikle cosinus-leddene som maclaurinrekker.
I en hyperbolsk geometri med uniform krumning kan Pytagoras' teorem uttrykkes som:
Ved å rekkeutvikle den hyperbolske funksjonen som en maclaurinrekke, vil (når man tar med de to første leddene) . Det kan da vises at når en hyperbolsk trekant blir lite (altså når a, b og c alle går mot null), vil den hyperbolske formen av teoremet gå mot den euklidske formen.
Historie
Opphavet og historien til Pytagoras' teorem har gjennom tidene skapt mye diskusjon, og mange teorier er fremsatt. Det kan i ettertiden være vanskelig å skille mellom fakta, tolkninger, grunngitte hypoteser og rene gjetninger. Kanskje har kunnskapen om sammenhengen mellom trekantsidene oppstått på ulike steder til ulike tider, uavhengig av hverandre. Samtidig har mye kunnskap også blitt utvekslet på tvers av landegrenser og tidsepoker, uten at vi i dag har kjennskap til dette. At en forståelse av teoremet har eksistert svært lenge før Pytagoras levde og virket, er nå allment akseptert.[30] Antagelig har forståelsen for teoremet vokst fram gjennom ulike stadier: en oppfatning av en rett vinkel, kunnskap om pytagoreiske tripler, kjennskap til sammenhengen mellom sidene i en rettvinklet trekant, kjennskap til sammenhengen mellom trekantvinkler og endelig teoremets bevis.
Det er verdt å være oppmerksom på at bruk av begrep som «Pytagoras teorem» og «bevis» i forbindelse med oldtidens matematikk lett kan skape feil inntrykk. Et utsagn som «xxx hadde et bevis for Pytagoras teorem tusen år før Pytagoras» kan som regel møtes med mange spørsmål, både når det gjelder kildebruk, tidsbestemmelse, formen på «teoremet» og kvaliteten av «beviset».
I forhistorisk matematikk
Oppmåling av europeiske og egyptiske megalittiske monumenter fra ca. 2500 år f.Kr. har ført til at det er framsatt teorier om at steinene i disse monumentene er plassert i former basert på rettvinklede trekanter med heltalssider.[31] Den nederlandske matematikeren Bartel Leendert van der Waerden gjetter på at de involverte pytagoreiske triplene ble funnet algebraisk.[32]
I babylonsk matematikk
Utdypende artikkel: Babylonsk matematikk

Funn av steintavler fra viser at babylonerne var godt fortrolige med ulike former for algebra, inkludert beregning av pytagoreiske tripler.[14] Det har vært spekulert i hva babylonerne brukte de pytagoreiske triplene til, og en mulighet kan ha vært i løsning av systemer av andregradsligninger med to ukjente. Babylonerne var også kjent med sammenhengen mellom en rettvinklet trekant og pytagoreiske tripler.
En svært viktig kilde til kunnskap er kileskrifttavlen Plimpton 322 fra Mesopotamia, skrevet i perioden 1822-1784 f.Kr.[14] Den antas å stamme fra den babylonske byen Larsa. Tavlen inneholder en tabell med fire kolonner og 15 rader. Kolonne nummer fire fra venstre nummererer radene, med tall fra 1 til 15. Kolonne nummer en er delvis ødelagt. Kolonne nummer to og tre har som overskrift henholdsvis «Bredde» og «Diagonal». Tabellen er tolket som å inneholde tall brukt for å konstruere pytagoreiske tripler, inkludert de følgende:
- .
En slik tolkning viser at babylonerne hadde metoder til å regne ut triplene, og tallene i tavlen kan indikere at de kjente Diofants konstruksjonsmåte.
En annen tavle i kileskrift, fra Hammurabi-dynastiet (1829–1530 f.Kr.), finnes nå i British Museum.[33] Tavlen inneholder et geometrisk problem, med løsning gitt i det seksagesimale tallsystem:[34][35]

| Originalteksten i oversettelse | Kommentarer |
| En stav: 0;30 GAR | 30/60 GAR = 1/2 GAR ≈ 3 m lang.[36] |
| foroven er den sunket 0;6 | Når toppen er senket 6/60 |
| nedentil har den fjernet seg | ..hvor langt har foten fjernet seg fra vertikalen? |
| 0;30 kvadrere: 0;15, skjønner? | (30/60)2 = 900/3500 = 15/60 |
| trekke 0;6 fra 0;30: 0;24, skjønner? | -6/60 + 30/60 = 24/60 |
| 0;24 kvadrere: 0;9,36, skjønner? | (24/60)2 = 576/3600 = 0;9,36 |
| trekk 0;9,36 fra 0;15: 0;5,24, skjønner? | - 576/3600 + 15/60 = 324/3600 = 0;5,24 |
| 0;5,24 har kvadratroten? 0;18 | (324/3600)−2 = 18/60 = 0;18 |
| 0;18 GAR har den fjernet seg ved bakken |
Løsningen i tavlen kan skrives som:
Dette svarer til Pytagoras' sats på formen . Fra denne kilden fremgår imidlertid ikke om babylonerne kjente noe matematisk bevis.
Ifølge historikeren Jamblikos skal Pytagoras ha oppholdt seg tolv år i Babylon.[37]
I egyptisk matematikk
Utdypende artikkel: Oldtidens egyptiske matematikk
En vanlig oppfatning er at egyptisk matematikk ikke nådde like langt som den babylonske, spesielt ikke innenfor algebra.[38][39] Om de utviklet ny geometrisk kunnskap er omdiskutert.[39] Gjennom landmåling la imidlertid egypterne et grunnlag for den etterfølgende greske geometrien, og egypterne har brukt pytagoreiske tripler til hjelp for å konstruere rette vinkler. En tau-ring med tolv ekvidistante knuter kan brukes til å danne en trekant med sidene 3,4,5, og derved danne en rett vinkel.
Det er lite funn av direkte kilder om egyptisk kjennskap til den pytagoreiske læresetningen. Verken Moskva-papyrusen eller Rhind-papyrusen nevner problemstillinger der denne er i bruk. Berlin-papyrus 6619 er skrevet mellom 2000 og 1786 f.Kr. i Mellomriket, og her forekommer fire ligninger som alle er basert på det pytagoreiske trippelet (3,4,5):[40]
Papyrusen inneholdet imidlertid ingen referanse til trekanter.
Mye av kunnskapen om egyptisk geometri kommer fra greske kilder.[41] Den antikke historikeren Herodot forteller om egyptisk landmåling og gir dette æren for opphavet til geometri. Proklos forteller at grekeren Thales reiste til Egypt og lærte geometri der. Også Pytagoras skal ha vært på reise i Egypt.[37] Demokrit skryter av at ingen har overgått ham i geometrisk kunnskap, ikke en gang de egyptiske «tau-strekkerne».[41]
I indisk matematikk
Utdypende artikkel: Indisk matematikk

Śulbasūtraene er en samling av indiske sutra-tekster fra engang mellom det 8. og 2. århundre f.Kr. Dette verket er en del av en større samling av religiøse tekster, og delen omtaler matematikk for å kunne konstruere brennalter og for å sette opp en kalender over religiøse høytider[42] Tittelen kan oversettes med «Regler for bruk av snoren».[43] Teksten lister fem pytagoreiske tripler, gir en form for Pytagoras' teorem og viser i tillegg at teoremet er gyldig for en likesidet trekant.[44][45][46]
Der eksisterer minst fire versjoner av Sulbasutraene, men geometri-beskrivelsen er relativt like i disse fire.[47] Versjonen som skal være laget av Baudhayana er anslått å være fra omkring 600 f.Kr, det vil si rundt hundre år før Pytagoras. Mye tyder på at kunnskapen som er samlet i teksten kan være betydelig eldre. Baudhayana-Sulbasutra drøfter flere problem der oppgaven er å konstruere en figur med samme areal som en eller flere andre figurer. I Sutra 50 gir teksten en oppskrift for å summere arealet av to kvadrat, illustrert ved figuren til høyre:
Hvis du vil slå sammen to ulike kvadrater til ett, ta det største kvadratet og legg til et bit av det største.Biten skal være laget med en side lik siden i det minste kvadratet. Diagonalen i denne biten er siden i det kombinerte kvadratet.
 Baudhayana Sutra 50[47]
Baudhayana Sutra 50[47]
Sutra 50, 51 og 54 gir sammen en form for godtgjøring for at Pytagoras' sats er riktig. Om dette kan gjelde som et generelt «bevis» er omdiskutert.[47][8]
Det er blitt foreslått at inderne hentet kunnskap fra Mesopotamia,[48] men også motsatt, at Mesopotamia fikk kunnskap fra India.[47]
I kinesisk matematikk
Utdypende artikkel: Kinesisk matematikk

Også kinesisk matematikk har i lang tid kjent til former for Pytagoras' teorem. Den eldste kjente kinesiske matematiske teksten er antagelig Zhoubi suanjing (Soluret og himmelens sirkler).[49] Tidfestingen av gamle kinesiske matematiske verk er svært usikker, og datering varierer sterkt i ulike kilder. Historien til Zhoubi suanjing kan gå helt tilbake til 1200 f.Kr, men verket har kanskje fått en endelig form en gang mellom 500 f.Kr. og 200 e.Kr. Innholdet er astronomiske beregninger, men også geometri for trekanter og litt om brøkregning. I likhet med både babylonske, indisk og egyptiske tekster, er dette en samling av problemer, med løsning. Blant de 246 problemene som er med i verket, inngår en figur som viser at kineserne kjente til den pytagoreiske læresetningen, med en trekant med sidelengder 3, 4 og 5.[45][50] Figuren er gjengitt til høyre. Den vertikale teksten til venstre for figuren er som følger:
- 勾股幂合以成弦幂
- gōu gǔ mì hé yǐ chéng xián mì
Summen av lengdene til kvadratene til høyden og basen er lik lengden til hypotenusen.
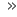 Soluret og himmelens sirkler[trenger referanse]
Soluret og himmelens sirkler[trenger referanse]
Nesten like gammelt som Zhoubi suanjing, og kanskje vel så innflytelsesrikt, er verket Chiu chang suan shu («Ni kapitler om den matematiske kunst»).[49][50] Også dette er en problem-samling, med løsning på 263 matematiske problemer. I det niende og siste kapittelet omtales pytagoreiske tripler og rette trekanter.[51] Et klassisk problem, som en også finner i indiske tekster, er «problemet med den brukne bambusen»:[50] Et bambustre som er 10 lengder høyt, knekker. Toppen når da bakken 3 lengder fra foten av stammen. Hvor høyt oppe er bambusen brukket? Løsningen krever bruk av Pytagoras' sats. Hvis er høyden til fra foten til knekkpunktet, så er
En kommentar til Chiu chang suan shu, med tittel Jiuchang suan shu, ble skrevet av Liu Hui i året 263 e.Kr. Her blir det gitt et bevis[bør utdypes] i kapittel 9.[52]
Den pytagoreiske læresetningen var kjent i Kina under navnet Gōugŭ (勾股), «base og høyde». For en trekant med sidene 3, 4 og 5 ble læresetningen kalt Gōugŭ-teoremet (勾股定理, Gōugŭ Dìnglĭ).[trenger referanse]
Pytagoras' rolle
Utdypende artikkel: Pythagoras

Svært lite håndfast er kjent om personen Pytagoras. Det er ikke funnet noe skriftlig verken fra ham eller fra miljøet rundt ham, og all kunnskap kommer fra senere omtale. Nøyaktig leveår for Pytagoras er ikke kjent, men det er antatt at han levde i perioden 580-475 f.Kr.[53] Beretninger om Pytagoras reiser til Babylonia og Egypt, fortalt av blant annet Jamblikos, har i ettertiden blitt møtt med både tillit og skepsis, men det er grunn til å tro at de inneholder en kjerne av sannhet.[37][54] Pytagoras ble leder for et filosofisk, matematisk og religiøst brorskap i Kroton, kjent som pytagoreerne.
Hvor mye kunnskap pytagoreerne hadde om sammenhengen mellom sidene i en rettvinklet trekant, er ikke kjent. Både Pytagoras og senere følgesvenner var nok fortrolige med pytagoreiske tripler, og etter tradisjonen skal kjennskapen til (3,4,5) ha kommet fra Egypt.[55] Om de hadde et bevis for sammenhengen mellom sidelengdene i en trekant, er omdiskutert. Thomas Heath gir flere bevis som kan ha vært brukt av pytagoreerne. Det er heller ikke kjent hva som ga støtet til kunnskapen om inkommensurable størrelser. Muligens kom dette fra arbeid med pentagramet, som var viktig for pytagoreerne, men det er også naturlig å anta at en likesidet trekant har vært involvert.
En tidlig kilde som tilegner teoremet til Pytagoras, skal ha vært en Apollodoros Arithmetikos, og han blir sitert av flere senere kilder.[8] Detaljer om Apollodoros liv er ikke kjent. Verset som blir sitert etter Apollodors er heller ikke entydig:
Da Pytagoras, som første, den berømte tegningen fant,
han brakte da som offer et guddommelig oksedyr.
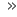
Apollodoros sier ingenting om hvilken «berømt tegning» han viser til. Det greske ordet brukt om «tegning» kan også tolkes som «teorem».[8] Fortellinger om dyreoffer som takk for kunnskap var også tidligere blitt knyttet til andre, inkludert til Thales. Diogenes Laertios (3. århundre f.Kr.) og flere andre går ut fra at verset gjelder oppdagelsen av Pytagoras' sats. Romeren Cicero (106-43 f.Kr.) bruker fortellingen om Pytagoras og dyreofferet, uten å spesifisere hvilken geometrisk oppdagelse det gjaldt. Han er imidlertid skeptisk, fordi dyreoffer ikke var godtatt blant pytagoreerne. En annen romer, Vitruvius (ca. 80-ca.15 f.Kr.), knytter fortellingen til oppdagelsen av det pytagoreiske trippelet (3,4,5). Plutark (45-120) var kritisk til å tolke verset i tilknytning til Pytagoras' teorem. Trass denne uenigheten, var det mange som i ettertid ga Pytagoras æren for å ha oppdaget teoremet.[8] Proklos i det femte århundre etter Kristus stadfester dette, uten selv å ta stilling til sannhetsinnholdet. Ifølge Proklos bør Euklid bli gitt største æren, for han var den ga bevis for teoremet.
I sitt store verk om historien til gresk matematikk, sier Thomas Heath i avsnittet om Pytagoras' teorem:
Though this is the proposition universally associated with the name of Pytagoras, no really thrustworthy evidence exists that it was actually discovered by him.
...
I would not go so far as to deny to Pytagoras the credit of the discovery of our proposition; nay, I like to believe that the tradition is right, and that it was really his.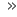 Thomas Heath[8]
Thomas Heath[8]
I ettertiden har det vært stor uenighet om Pytagoras' rolle, og flere hypoteser er gjeldende:
- Pytagoras overtok satsen fra babylonerne. Han var kun en formidler av orientalsk kunnskap til grekerne. Dette er synet til vitenskapshistorikeren Walter Burkert.[56]
- Pytagoras oppdaget og beviste satsen uavhengig av orientalsk matematikk. Dette var en vanlig oppfatning i antikken og er også synet til vitenskapshistorikeren Leonid Zhmud.[57][58]
- Pytagoras støttet seg til orientalske kilder, men var den første som fant et bevis. Egypterne og babylonerne var primært interessert i satsens anvendelse og ikke i et generelt bevis.
- Pytagoras hadde selv få eller ingen bidrag. Andre pytagoreere kan på et senere tidspunkt ha funnet et bevis og så har dette blitt knyttet til Pytagoras.
Oppfatningen til Thomas Heath ligger kanskje et sted mellom de to siste hypotesene.
Euklids rolle
Utdypende artikkel: Evklid
Euklid hadde mesteparten av sitt virke i Alexandria, omkring 300 f.Kr. Beviset som Euklid bruker for Pytagoras' teorem i I.47 er antagelig hans eget.[59] Det betyr ikke at det ikke eksisterte eldre bevis eller at Euklid ikke kjente til disse. Euklid bygger opp Elementer svært systematisk, og beviser satsene steg for steg. Beviset for I.47 ble antagelig valgt fordi det ikke trengte bruk av formlike figurer og forhold mellom lengder. Dette emnet ble først introdusert i bok V. Pytagoras' teorem og det omvendte teoremet avslutter bok I, som høydepunkt. Så om beviset for I.47 i dag kan synes unødig komplisert, så er Euklids fortjeneste at han greidde å gjennomføre dette kun basert på innholdet i bok I.
Euklids Elementer ble antagelig skrevet som en lærebok og ikke som et forsøk på å samle all kjent geometrisk kunnskap eller presentere ny kunnskap.[60] Ingenting blir nevnt om opphavet til innholdet, og heller ikke Pytagoras er nevnt. Det er antatt at store deler av innholdet i bok I, II, IV og VI var kjent for pytagoreerne.[61] Euklid gjør ingen krav på originalitet, men han har antagelig laget nye bevis der dette har vært nødvendig for sammenhengen.[60] Det store bidraget til Euklid var den systematiske oppbyggingen av teorien, der alt blir stringent bevist.
In rectangulis triangulisquadratum, quod a latere rectum angulum subtendentedescribitur, aequale est eis, quae a lateribus rectumangulum continentibus describuntur.
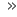 Euklid I.47 i latinsk versjon[55]
Euklid I.47 i latinsk versjon[55]
I rettvinklede trekanter er kvadratet på siden motstående til den rette vinkelen lik kvadratene på sidene som avgrenser den rette vinkelen
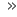 Euklid I.47 i norsk omsetting etter T. Heath[62]
Euklid I.47 i norsk omsetting etter T. Heath[62]
I kulturen
Pytagoras' læresetning er gjennom tidene referert til eller gjengitt i en lang rekke sammenhenger:
- Et vers i «Generalmajorens sang» i musikalen The Pirates of Penzance av Gilbert og Sullivan har referansen: «About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse.»
- Fugleskremselet Scarecrow i Trollmannen fra Oz gir en referanse til teoremet idet han mottar eksamensbevis fra trollmannen. Han fremviser umiddelbart sin «kunnskap» ved å gjengi en radbrukket og ukorrekt versjon av teoremet: «Summen av kvadratroten på to tilfeldige sider av en likesidet trekant er lik kvadratroten av den siste siden. Oh, hurra! Jeg har vel en hjerne!»
- I en episode av The Simpsons, etter å ha funnet Henry Kissingers briller på toalettet i Springfield Nuclear Power Plant, tar Homer dem på og gjengir Oz Scarecrows forenklede versjon av teoremet. En mann i nærheten roper ut: «Det er en rettvinklet trekant – din idiot!»
- I talesynteseprogramvaren i Mac OS X finnes en stemme kalt Ralph, som gjengir teoremet i en eksempeltekst.
- For en Past Master bruker frimuerereet symbol som er et diagram Euklid brukte i sitt bevis av teoremet.
- I Neal Stephensons spekulative fiction Anathem er Pytagoras' teorem gjengitt som the Adrakhonic theorem. Et geometrisk bevis er gjengitt på et romskip, for å vise eiernes kunnskap om matematikk.
- I den engelske versjonen av den syttende boken om Asterix, The Mansions of the Gods, benytter Julius Cæsar seg av tjenesten til arkitekten Squareonthehypotenus (Kvadratetpåhypotenusen).
- I 2000 utga Uganda en mynt med form som en rett trekant. Myntens bakside har en illustrasjon av Pytagoras og Pytagoras' teorem, sammen med teksten «Pythagoras Millennium».[63]
- Hellas, Japan, San Marino, Sierra Leone og Surinam er alle land som har gitt ut frimerker med motiver av Pytagoras og Pytagoras' teorem.[64]
Historien om dyreofferet til Pytagoras har inspirert dikteren Adelbert von Chamisso til en sonett, Vom pythagoreischen Lehrsatz, der første vers lyder:[trenger referanse]
Die Wahrheit, sie besteht in Ewigkeit,
Wenn erst die blöde Welt ihr Licht erkannt;
Der Lehrsatz nach Pythagoras benannt
Gilt heute, wie er galt zu seiner Zeit.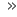
Oversatt til norsk kan det gjengis slik:
Evighet er Sannhetens byggekloss,
At verden så lyset, er hva det krevde;
Den læresetningen Pytagoras ga oss
Gjelder like mye i dag som da han levde.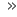
Referanser
- ^ a b Judith D. Sally, Paul Sally (2007). Roots to research: A vertical development of mathematical problems (engelsk). American Mathematical Society Bookstore. s. 63ff. ISBN 978-0-8218-4403-8.
- ^ E.S. Loomis: The Pythagorean proposition s.1
- ^ a b C.B.Boyer: A history of mathematics s.119
- ^ «Euclid Elements. Proposition 47» (engelsk). Persus Digital Library. Besøkt 12. mars 2021.
- ^ E.S. Loomis: The Pythagorean proposition s.120
- ^ David Eugene Smith (1925). History of mathematics (engelsk). II. Ginn and Company. s. 284.
- ^ E.S. Loomis: The Pythagorean proposition s.24
- ^ a b c d e f g T. Heath A history of Greek mathematics (Vol. I) s.144-149
- ^ «Pythagorean theorem» (engelsk). Angie Head, University of Georgia. Besøkt 12. mars 2021.
- ^ «Mathematical Treasure: James A. Garfield's Proof of the Pythagorean Theorem» (engelsk). Mathematical Association of America. Besøkt 12. mars 2021.
- ^ «Pythagorean theorem. Proof 4» (engelsk). Cut the Knot. Besøkt 13. mars 2021.
- ^ «Euclid Elements. Proposition 48» (engelsk). Persus Digital Library. Besøkt 12. mars 2021.
- ^ G.H. Hardy, E.W. Wright (2008). An introduction to the theory of numbers. Oxford: Oxford University Press. s. 245-247. ISBN 978-0-19-921985-8.
- ^ a b c A. Holme: Matematikkens historie (Bind 1) s.21ff
- ^ T. Heath A history of Greek mathematics (Vol. I) s.81
- ^ A. Holme: Matematikkens historie (Bind 1) s.49
- ^ T. Heath A history of Greek mathematics (Vol. I) s.154-157
- ^ T. Heath A history of Greek mathematics (Vol. I) s.65
- ^ T. Heath A history of Greek mathematics (Vol. I) s.402ff
- ^ R.V Churchill, J.W. Brown, R.F. Verhey (1974). Complex variables and applications. Tokyo: McGraw-Hill Kogakusha. s. 7. ISBN 0-07-010855-2.
- ^ Ernest Julius Wilczynski, Herbert Ellsworth Slaught (1914). Plane trigonometry and applications. Allyn and Bacon. s. 85ff.
- ^ Matematikk for den videregående skole. Oslo: Gyldendal. 1986. s. 25. ISBN 82-05-16032-5.
- ^ «On the theorem of Phytagoras» (PDF). Edsger Dijkstra, University of Texas. Besøkt 13. mars 2021.
- ^ A. Holme: Matematikkens historie (Bind 1) s.309
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.397
- ^ T. Heath A history of Greek mathematics (Vol. II) s.369-371
- ^ «De Gua's theorem». Wolfram MathWorld. Besøkt 14. mars 2021.
- ^ Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
- ^ D.J. Struik (1961). Lectures on classical differential geometry. New York: Dover Publications. s. 5-10. ISBN 0-486-65609-8.
- ^ A. Holme: Matematikkens historie (Bind 1) s.26
- ^ «Megalithic monuments». Arkivert fra originalen 6. juli 2011. Besøkt 17. januar 2010.
- ^ B.L. van der Waerden: Geometry and algebra ... s.??
- ^ «Tablet 85196». British Museum. Besøkt 14. mars 2021.
- ^ H. Geriche: Mathematik in Antike und Orient s.33f
- ^ K. Vogel: Vorgriechische Mathematik s.67f
- ^ K. Vogel: Vorgriechische Mathematik s.20
- ^ a b c A. Holme: Matematikkens historie (Bind 1) s.169
- ^ A. Holme: Matematikkens historie (Bind 1) s.59ff
- ^ a b C.B.Boyer: A history of mathematics s.40
- ^ Stephen Hawking (2005). God created the integers: The mathematical breakthroughs that changed history. Greenworld Books. ISBN 978-0762419227.
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.123ff
- ^ Swami Vishnu (2018). Vedic science & history. Gosai Publishers. s. 65f. ISBN 978-8-1926601-3-4.
- ^ A. Holme: Matematikkens historie (Bind 1) s.122
- ^ H. Geriche: Mathematik in Antike und Orient s.68
- ^ a b Oskar Becker (1966). Das mathematische Denken der Antike. Göttingen: Vandenhoeck & Ruprecht. s. 55f.
- ^ Euclid: The thirteen books of... s.360-364
- ^ a b c d David W. Henderson, Daina Tamina. Experiencing geometry. Project Euclid. s. 174ff. ISBN 978-0131437487.
- ^ C.B.Boyer: A history of mathematics s.229
- ^ a b C.B.Boyer: A history of mathematics s.217
- ^ a b c A. Holme: Matematikkens historie (Bind 1) s.87
- ^ F. Swetz, T.I. Kao: Was Pythagoras Chinese? ... s.??
- ^ Karine Chemla, Guo Shuchun (2005). Les neuf chapitres. Le classique de la Chine ancienne et ses commentaires. Édition critique. Dunod. s. 680. ISBN 978-2100495894.
- ^ A. Holme: Matematikkens historie (Bind 1) s.164
- ^ A. Holme: Matematikkens historie (Bind 1) s.178f
- ^ a b E.S. Loomis: The Pythagorean proposition s.4
- ^ Walter Burkert (1962). Weisheit und Wissenschaft. Nürnberg. s. 405f, 441ff.
- ^ Leonid Zhmud (1997). Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Berlin. s. 141-151, 160-163.
- ^ Euclid: The thirteen books of... s.350-360
- ^ T. Heath A history of Greek mathematics (Vol. I) s.378
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.354ff
- ^ T. Heath A history of Greek mathematics (Vol. I) s.201
- ^ A. Holme: Matematikkens historie (Bind 1) s.264
- ^ «Le Saviez-vous ?». Arkivert fra originalen 21. september 2009.
- ^ Miller, Jeff (3. august 2007). «Images of mathematicians on postage stamps». Besøkt 6. august 2007.
Litteratur
På norsk:
- Holme, Audun (2008). Matematikkens historie. 1. Bergen: Fagbokforlaget. ISBN 978-82-450-0697-1.
På engelsk:
- Boyer, Carl B. (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
- Euclid (1956). The thirteen books of the Elements. Translated with an introduction and commentary by Sir Thomas L. Heath. I, II og III. Dover. ISBN 978-0-486-60088-8.
- Heath, Thomas (1981). A history of Greek mathematics. I og II. New York: Dover Publications. ISBN 0-486-24073-8.
- Loomis, Elisha Scott (1968). The Pythagorean proposition (PDF). Washington, D.C: The National Council of Teachers of Mathematics. ISBN 978-0873530361.
- Maor, Eli (2007). The Pythagorean theorem: A 4,000-Year History. =Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Stillwell, John (1989). Mathematics and its history. Springer-Verlag. ISBN 3-540-96981-0.
- Swetz, Frank, Kao, T. I. (1977). Was Pythagoras Chinese? An examination of right triangle theory in ancient China. Pennsylvania State University Press.
- van der Waerden, B.L. (1983). Geometry and algebra in ancient civilizations. Springer. ISBN 978-0387121598.
På tysk:
- Fraedrich, Anna M. (1994). Die Satzgruppe des Pythagoras. Heidelberg: Spektrum Akademischer Verlag. ISBN 3-86025-669-6.
- Gericke, Helmuth (1984). Mathematik in Antike und Orient. Berlin: Springer. ISBN 978-3-642-68630-6.
- Vogel, Kurt (1959). Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Hannover: Hermann Schroedel.
Eksterne lenker
- (en) Pythagorean theorem – kategori av bilder, video eller lyd på Commons
- «Pythagorean Theorem» (engelsk). Cut the Knot. Besøkt 15. mars 2021. Mer enn 70 bevis
- «Pythagoras's Theorem in Babylonian Mathematics» (engelsk). MacTutor. Besøkt 15. mars 2021.
- «Pythagorean Theorem» (engelsk). Wolfram MathWorld. Besøkt 15. mars 2021.
- «Euclid's Elements» (engelsk). Clark University, USA. Besøkt 15. mars 2021.



























































![{\displaystyle {\begin{alignedat}{2}{\frac {(a+b)^{2}}{2}}\ &=\ ab+{\frac {c^{2}}{2}}\\[5pt]a^{2}+2ab+b^{2}\ &=\ 2ab+c^{2}\\[5pt]a^{2}+b^{2}\ &=\ c^{2}.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53c9d6e9f45e0666c18df9e1b831ae19813fad89)














&=\left(\ (4m^{2},(m^{2}-1)^{2},(m^{2}+1)^{2}\ \right)\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cfd776e81fff12cd2769f0e0af12d84b3335b0)








































![{\displaystyle {\begin{alignedat}{2}&{\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\\[7pt]&\Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C=C\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c57c9fedc6ac7e6528510a2309ef2899db16f59a)

















![{\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} \qquad t\in [a,b]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b241899d3a43740404e9505d6d5069ab22008dc)











