Euklidsk rom

Et euklidsk rom eller et kartesisk rom er i matematikk et reelt endeligdimensjonalt vektorrom der det er definert et såkalt euklidsk indreprodukt og en tilhørende norm.[1][2] Har rommet n dimensjononer, betegnes det vanligvis som En . Definisjonen av indreproduktet medfører at euklidske rom har egenskaper som svarer til de vi er fortrolig med fra euklidsk geometri. Blant annet gjelder generaliseringer av Pythagoras’ læresetning og parallellogramloven.
Definisjonen av et Euklidske rom kan variere, og noen forfattere utvider definisjonen til også å omfatte komplekse tallmengder.[1] Alternativt defineres også euklidske rom mer generelt som et endelig- eller uendeligdimensjonalt (reelt) indreproduktrom, det vil si som et vektorrom utstyrt med et vilkårlig indreprodukt.[1][3] Denne alternative definisjonen er ikke så utbredt.[1]
Den reelle tallinjen R er et endimensjonalt euklidsk rom E1. Tilsvarende er planet R2 og rommet R3 henholdsvis et todimensjonalt E2 og et tredimensjonalt E3 euklidsk rom når disse rommene er utstyrte med euklidske indreprodukt. Definisjonen av et euklidsk rom abstraherer egenskaper kjent fra disse vektorrommene og gjør det også mulig å generalisere egenskapene til rom av høyere dimensjon. Et vilkårlig n-dimensjonalt euklidsk rom er isomorft med Rn, det vil si har samme struktur som Rn. Notasjonen En er vanlig brukt for et n-dimensjonalt euklidsk rom, men Rn kan også benyttes når det går klart frem av sammenhengen at rommet har et indreprodukt.
Løst kan en beskrive euklidske rom som mengder eller rom der de euklidske geometriske postulatene er oppfylt. Euklid av Alexandria var en gresk matematiker som levde rundt 300 f.Kr. Navnet kartesiske rom er oppkalt etter den franske matematikeren René Descartes.
Formell definisjon[rediger | rediger kilde]
Et euklidsk vektorrom En med dimensjon n er isomorft med det reelle vektorrommet Rn som har samme dimensjon n.[4] At rommene er isomorfe vil si at de har samme struktur, og en kan dermed studere strukturen i et vilkårlig euklidske rom ved å studere det tilsvarende vektorrommet.
En vektor x i dette n-dimensjonale vektorrommet kan alltid angis ved n reelle tall (x1, x2, .... , xn) som
Disse samlingene av tall kalles ofte for n-tupler og utgjør koordinatene til vektorene. De kalles derfor også ofte for koordinatvektorer. Vektorene kan også oppfattes som punkt i vektorrommet og vil da kalles for posisjonsvektorer for de tilsvarende punktene.
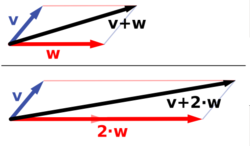
Vektorromsoperasjonene i En defineres på samme måte som for Rn. To vektorer v og w kan adderes til å gi en ny vektor
og hver vektor kan multipliseres med et reelt tall, a w = (aw1, aw2, .... , awn). Komponentene til nullvektoren er alle lik null.
Vektorrommet Rn har en standardbasis definert ved vektorene
Disse kan også benyttes i det euklidske rommet En. En vilkårlig vektor u kan derfor skrives som
Komponentene xi med hensyn til denne standardbasisen er da de kartesiske koordinatene til vektoren eller det tilsvarende punktet. Ved å danne lineære kombinasjoner av disse basisvektorene, fremkommer en ny basis. Komponentene i denne nye basisen vil da i alminnelighet bli forandret og kalles mer generelt for rettlinjete koordinater.
Indre produkt[rediger | rediger kilde]
Dette vektorrommet blir euklidsk når det utstyres med et indreprodukt. For de to vektorene x og y er dette i standardbasisen definert som[2]
Det kalles for det euklidske skalarproduktet eller ganske enkelt for skalarproduktet. For vektorene som utgjør standardbasisen betyr det at de har indreproduktene
hvor høyresiden er uttrykt ved Kronecker-deltaet
Fra indreproduktet følger at lengden eller den euklidske normen til en vektor kan defineres som
Lengden til basisvektorene er derfor lik en. De kalles derfor også ofte for enhetsvektorer.
Avstanden mellom to punkt spesifisert ved posisjonsvektorene x og y er nå gitt som
og definerer den metrikken i det euklidiske rommet. Dette kan også forstås som et avstandsmål mellom de tilsvarende vektorene.
Noen geometriske egenskaper[rediger | rediger kilde]

Fra definisjonen av skalarproduktet følger at lengden av vektoren x + y er gitt ved
mens kvadratet av lengden til differansen mellom de to samme vektorene er
Legges disse to ligningene sammen, finner man at
Hvis vektorene x og y representerer siden i et parallellogram, er dette resultatet et uttrykk for parallellogramloven da vektorene x + y og x + y utgjør diagonalene i parallellogrammet. Summen av de fire kvadrerte sidene i parallellogrammet er lik summen av de to kvadrerte diagonalene.
Vinkler[rediger | rediger kilde]

Definisjonen av indreproduktet gjør at egenskaper til vinkler mellom vektorer kan generaliseres. Fra det 3-dimensjonale euklidske vektorrommet kan man i alminnelighet definere vinkelen θ mellom to vektorer x og y ved skalarproduktet
Er dette produktet lik null, sies vektoren å være ortogonale eller stå normalt på hverandre. Vinkelen mellom dem er da 90° som tilsvarer π/2 radianer. Da er cosθ = 0 og x⋅y = 0. Dette gjelder for enhetsvektorene i standardbasisen. De sies derfor å være ortonormerte.
Vektorsummen x + y representerer siden i en trekant hvor x og y er de to andre sidene. Kvadreres denne summen, har man nå
som er et uttrykk for cosinussetningen i det euklidske rommet. Står vektorene x og y vinkelrett på hverandre slik at θ = 90°, forenkles resultatet til Pythagoras’ læresetning
for en rettvinklet trekant bestående av en hypotenus med lengde |x + y| og kateter |x| og |y|. Denne loven kan på et visst vis sies å definere euklidsk geometri.
Matriseeksempel[rediger | rediger kilde]
Mengden av reelle 2 × 2 matriser utgjør et vektorrom, med den vanlige matriseoperasjonene for addisjon og skalarmultiplikasjon. Med passende definisjon av indreprodukt og norm kan dette bli et euklidsk vektorrom. En matrise A i dette vektorrommet kan skrives på formen
Som basis kan en velge matrisene
Vektorrommet vil være et euklidsk vektorrom dersom det utstyres med det såkalte Froebenius-skalarproduktet, definert ved[5]
Den tilhørende Froebeniusnormen er definert ved
Vektorrommet har dimensjon 4 og er altså isomorft med R4. Merk at matriserommet ikke er identisk med R4.
Euklidsk og ikke-euklidsk geometri[rediger | rediger kilde]

Rundt 300 f.Kr. studerte den greske matematikeren Euklid forholdene mellom avstander og vinkler, først i planet (en idealisert flat overflate) og deretter i rommet. Et eksempel på et slikt forhold er at summen av vinklene i en trekant alltid er lik 180 grader. I dag er denne samlingen av forhold kjent som to- eller tredimensjonal euklidisk geometri.
I klassisk gresk geometri ble det euklidske planet og de tredimensjonale rommene definert ved bruk av en rekke aksiomer, og rommenes andre egenskaper ble utledet som teoremer. I moderne matematikk er det mer vanlig å definere euklidsk rom ved bruk av kartesiske koordinater og prinsippene for analytisk geometri. Dette gjør at man kan bruke verktøyene i algebra og matematisk analyse til å løse geometriske problemer, og har den fordelen at den enkelt generaliserer til euklidske rom med mer enn tre dimensjoner.
En avgjørende egenskap ved euklidsk rom er dets «flathet». Det eksisterer vektorrom som ikke er euklidske, for eksempel knyttet til geometri på en kuleoverflate. En trekant på en kule vil (når den er passende definert) ha vinkler som til sammen kan summeres til mer enn 180 grader.
Topologien til euklidsk rom[rediger | rediger kilde]
Ettersom et euklidsk rom er et metrisk rom, er det også et topologisk rom, med den naturlige topologien som følger av metrikken. Metrikktopologien på Rn kalles den euklidske topologien.[6]
En mengde er åpen i den euklidske topologien hvis og bare hvis mengden inneholder en åpen kule om ethvert av punktene. Den euklidske topologien er ekvivalent med produkttopologien for det kartesiske produktet (R × R × ... × R) , med n faktorer.
Et viktig resultat om topologien til Rn er Brouwers teorem for domeneinvarians: Enhver delmengde av Rn (med deltopologien) som er homeomorft med en annen åpen delmengde av Rn, er selv åpen. En umiddelbar følge av dette er at Rm ikke er homeomorft med Rn hvis m ≠ n – et intuitivt resultat som ikke så lett lar seg bevise.
Generaliseringer[rediger | rediger kilde]
Et Hilbertrom kan betraktes som en generalisering av et euklidsk rom til å omfatte også uendeligdimensjonale rom. Et Hilbertrom er et komplett indreproduktrom, det vil si at alle Cauchyfølger konvergerer i rommet.[7] Et Hilbertrom kan være definert med reelle eller komplekse vektorer. Dersom et euklidske rom defineres som et vilkårlig (reelt) indreproduktrom, så er dette sammenfallende med et (reelt) pre-Hilbertrom. Forskjellen med et Hilbertrom er kravet om kompletthet.
I moderne matematikk er euklidsk rom prototypen for andre mer kompliserte geometriske objekter. Eksempelvis er en glatt mangfoldighet et Hausdorff-rom, som er lokalt diffeomorft med euklidsk rom. Diffeomorfier bevarer ikke avstand og indreprodukt, så disse begrepene går tapt på en glatt mangfoldighet. Tilføyer man imidlertid mangfoldigheten et glatt indreprodukt på mangfoldighetens tangentrom, får en det som kalles en riemannsk mangfoldighet. Med andre ord er en riemannsk mangfoldighet et rom og resultat av å deformere og sammenlappe euklidske rom. Et slikt rom har også begreper som avstander og vinkler, men oppfører seg på en krum ikke-euklidsk måte. Den enkleste riemannske mangfoldigheten består av Rn med et konstant indreprodukt, og det er i seg selv stort sett identisk med det euklidske rom.
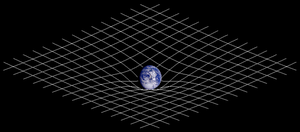
Endrer man det euklidske rommet slik at dets indreprodukt blir negativt i en eller flere retninger, får en frem det som kalles pseudoeuklidsk rom. Glatte mangfoldigheter basert på disse rommene kalles pseudoriemannske mangfoldigheter. Deres kanskje mest kjente anvendelse er i relativitetsteorien, hvor materieløst romtid representeres ved et flatt pseudoeuklidsk rom kalt Minkowski-rommet, og hvor romtider med materie representeres ved andre pseudoriemannske mangfoldigheter og tyngdekraften svarer til krumningen av en slik mangfoldighet.
Vårt univers, som er underlagt relativitetsteorien, er ikke euklidsk. Dette er avgjørende i teoretiske betraktninger i astronomi og kosmologi, samt i praktiske problemstillinger som global posisjonering og navigasjon av fly. Ikke desto mindre kan en euklidsk modell brukes i løsningen av mange andre problemer med tilstrekkelig presisjon.
Se også[rediger | rediger kilde]
Referanser[rediger | rediger kilde]
- ^ a b c d E.J.Borowski, J.M.Borwein (1989). Dictionary of mathematics. Glasgow: Collins. s. 200. ISBN 0-00-434347-6. [Euclidean space]
- ^ a b W.Rudin: Principles of mathematical analysis, s.16
- ^ R.D.Milne: Applied functional analysis..., s.181
- ^ R.D.Milne: Applied functional analysis..., s.34
- ^ Gene Golub, Charles van Loan (1996). Matrix computations. Baltimore: Johns Hopkins University Press. s. 14. ISBN 0-8018-5414-8.
- ^ John G. Hocking, Gail S. Young (1961). Topology. Mineola, N.Y.: Dover Publications. s. 10. ISBN 0-486-65676-4.
- ^ R.D.Milne: Applied functional analysis..., s.184
Litteratur[rediger | rediger kilde]
- Walter Rudin (1976). Principles of mathematical analysis. Singapore: McGraw-Hill International Book Co. ISBN 0-07-085613-3.
- Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
- Kelley, John L. (1975). General Topology. Springer-Verlag. ISBN 0-387-90125-6.
- Munkres, James (1999). Topology. Prentice-Hall. ISBN 0-13-181629-2.






















