Ortogonalitet

AB og CD er ortogonale i forhold til hverandre.

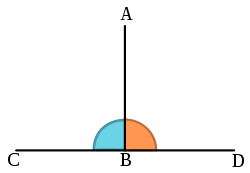
Ortogonalitet er i matematikken en egenskap ved vektorer og funksjoner. To vektorer/funksjoner er ortogonale dersom de er uavhengige av hverandre (at den ene vektoren/funksjonen ikke kan benyttes til å beskrive den andre). Dette betyr at vektorene står vinkelrett på hverandre, noe som er enklest å forestille seg i vanlige to- og tre-dimensjonale vektorsystemer.

Definisjoner

Om to vektorer x og y er ortogonale, er indreproduktet mellom dem lik null: $x\cdot y=0$. For å uttrykke ortogonalitet matematisk skrives dette som $x\perp y$.

At to funksjoner $f(x)$ og $g(x)$ er ortogonale i intervallet $[a,b]$ defineres som at indreproduktet mellom dem er lik null:

$\langle f,g\rangle =\int _{a}^{b}f(x)\cdot g(x)dx=0$.

For eksempel er sinus og cosinus ortogonale i området $[0,2\pi ]$.

Denne artikkelen er en spire. Du kan hjelpe Wikipedia ved å utvide den.