Pytagoras’ læresetning
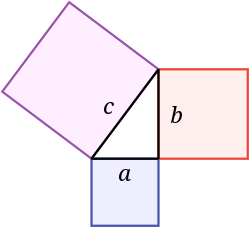
Pytagoras’ læresetning eller den pytagoreiske læresetning er i euklidsk geometri et fundamentalt teorem om sammenhengen mellom sidelengdene i en rettvinklet trekant:
- «I en rettvinklet trekant er summen av kvadratene på katetene lik kvadratet på hypotenusen.»
De to katetene er de korteste sidene i trekanten, og hypotenusen er den lengste. Den rette vinkelen er motstående til hypotenusen. Kaller man lengdene av katetene henholdsvis og samt lengden av hypotenusen for , så kan læresetningen uttrykkes som en ligning, ofte kalt Pytagoras ligning:[1]
- .
Heltall som oppfyller Pytagoras’ læresetning kalles pytagoreiske tripler. Et velkjent trippel er (3,4,5). Dersom sidelengdene i en trekant danner et pytagoreiske trippel, så er trekanten rettvinklet.
Det eksisterer mange generaliseringer av Pytagoras’ teorem. En generalisering til en vilkårlig trekant kalles den utvidede pytagoreiske læresetning eller cosinussetningen.
Det historiske opphavet til teoremet er bare mangelfullt kjent og har vært gjenstand for mye diskusjon. Navnet har teoremet fått fordi mange tradisjonelt har knyttet læresetningen til den greske matematikeren Pytagoras, som levde omkring 500 f.Kr. Det eksisterer imidlertid ikke gode indikasjoner eller bevis for at han eller noen av hans følgesvenner skal ha vært opphavsmann til teoremet. Pytagoreiske tripler og andre former for teoremet har vært kjent i babylonsk, egyptisk, kinesisk og indisk matematikk lenge før pytagoreerne. Kanskje har læresetningen blitt oppdaget flere steder og til flere tider uavhengig av hverandre. Det eldste deduktive bevis vi kjenner, er fra Euklids Elementer, skrevet omkring 300 f.Kr. I dag eksisterer det en lang rekke alternative bevis for teoremet.
Bevis[rediger | rediger kilde]


Pytagoras’ læresetning antas å være et av de teoremene i matematikk som er bevist på flest alternative måter. Boken Pythagorean Proposition av Elisha Scott Loomis inneholder hele 370 bevis.[2] I boken er 109 bevis karakterisert som algebraiske og 255 som geometriske. De resterende seks er basert på vektorregning eller dynamiske argument. Et geometrisk bevis bygger ifølge Loomis på sammenligning av arealet til de tre kvadratene konstruert fra sidelengdene, mens et aritmetisk er basert på lineære relasjoner mellom sidelengder eller areal, for eksempel ved bruk av formlike trekanter. Denne inndelingen er kanskje ikke entydig, og mange bevis har innslag av både geometri og algebra.
Euklids bevis[rediger | rediger kilde]
I Euklids Elementer, teorem 47 i bok I, finner man det eldste kjente beviset for Pytagoras’ teorem.[3][4] Det er vanlig å referere til Euklids bøker med romertall for bindet og et vanlig tall for den gjeldende satsen, slik at Pytagoras’ teorem er I.47. Beviset for I.47 er basert på en sammenligning av areal.
La , og være hjørnene i en rettvinklet trekant, med den rette vinkel ved som vist på figuren. Til hver side i trekanten er det tegnet et kvadrat. En normal fra hjørnet til hypotenusen deler kvadratet på hypotenusen i to rektangler, på figure vist i blått og rosa. Euklid beviste setningen ved å vise at arealet til hver av de to minste kvadratene er lik arealet av ett av rektanglene, vist med fargene i figuren. Arealsummen av de to minste kvadratene er dermed lik arealet til det største kvadratet.
Beviset bygger på flere hjelpesetninger, som Euklid viser tidligere i bok I. Disse vil bli brukt videre, uten bevis her.
- Hvis to trekanter er slik at to sider i den ene er lik tilsvarende to sider i den andre, og den mellomliggende vinkel er lik i begge, så er trekantene kongruente.
- Arealet av en gitt trekant er lik halvparten av arealet i et vilkårlig parallellogram med samme grunnlinje og høyde.
- Arealet av et rektangel er lik produktet av to tilstøtende sider.
- Arealet av et kvadrat er lik produktet av to sider.
Beviset er som følger:
- La være en rettvinklet trekant, med den rette vinkelen gitt ved .
- På hver av sidene , og tegnes kvadrater, henholdsvis , og .
- Fra trekkes en linje parallell med og . Den krysser og i rett vinkel ved henholdsvis og .
- Forbind og . Derved dannes trekantene og .
- Vinklene og er begge rette. Punktene , og ligger derfor på samme linje. Tilsvarende ligger , og på en rett linje.
- Vinklene og er begge rette. Dermed er lik , siden begge er summen av en rett vinkel og den felles .
- Siden og er tilsvarende like med og , må trekanten være kongruent med trekanten .
- Ved bruk av hjelpesetning nr.2 må rektangelet være dobbelt så stort som trekanten .
- Ved bruk av hjelpesetning nr.2 må rektangelet være dobbelt så stort som trekanten .
- Dermed må rektangelet ha samme areal som kvadratet , det vil si at .
- Tilsvarende kan det vises at rektangelet må ha samme areal som kvadratet , det vil si at .
- Ved å addere disse to resultatene: .
- Siden , så er .
- Dermed er , siden er et kvadrat.
Beviset har tidligere vært pensum i norsk realskole.[trenger referanse] Det finnes enklere bevis, men gjennomgang av fremgangsmåten kan være en egnet øvelse i matematisk tenkning.
Figuren til Euklids bevis, med hjelpelinjer til alle fire kvadrater, er berømt. Den er blitt beskrevet som en «vindmølle», en «brudestol» og en «påfugl-hale».[3] Også navnet pons asinorum er blitt brukt om figuren.[5] Dette latinske utrrykket betyr «eselbroen» eller «idiotbroen», og uttrykket knyttes vanligvis til en annen Euklid-figur, brukt i forbindelse med Elementer I.5.[6]
Bevis ved bruk av formlike trekanter[rediger | rediger kilde]

Mange av bevisene for Pytagoras’ setning er basert på forhold mellom sidelengder i to formlike trekanter. Elisha Scott Loomis omtaler dette som det korteste av alle Pytagoras-bevisene og kaller det også for «Legendre-beviset».[7] En lærebok i geometri fra 1858, basert på arbeid av Adrien-Marie Legendre, gjengir beviset. Thomas Heath foreslår dette som ett alternativ for et bevis som kan ha vært brukt av pytagoreerne.[8]
La være en rettvinklet trekant. Den rette vinkelen er ved , slik figuren viser. Høyden fra hjørnet treffer siden i fotpunktet . Trekanten er formlik med trekanten , da begge er rettvinklede og vinkelen ved er felles. Tilsvarende er trekanten formlik med . Til sammen resulterer dette i følgende forhold mellom sidelengder:
Dette kan skrives som
Summasjon av de to uttrykkene gir
Garfields bevis[rediger | rediger kilde]
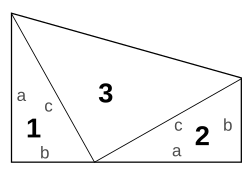
James Garfield er opphavsmann for det følgende beviset.[9][10] Han var jurist og medlem av den amerikanske Kongressen, og han oppdaget beviset i 1876 som følge av en matematisk diskusjon med andre kongressmedlemmer. Garfield ble president i USA i 1881, men han ble skutt og drept etter bare fire måneder i embetet.
Arealet av et generelt trapes med høyde og lengder av de to parallelle sidene og er gitt ved
Da er arealet av trapeset vist i figuren:
Trekant 1 og 2 er identiske, med areal
- .
Trekant 3 er rettvinklet, og arealet er lik halvparten av kvadratet på hypotenusen:
Et alternativt uttrykk for arealet til trapeset finner en ved å summere arealene til de tre trekantene:
En sammenstillingen av de to uttrykkene for trapesarealet gir
Bevis ved reorganisering[rediger | rediger kilde]

Det eksisterer flere bevis basert på å reorganisere areal. Et eksempel er vist i figuren til venstre. De to store kvadratene i figuren er like store, begge med sidelengde . De to kvadratene skiller seg kun ved den innvendige plasseringen av de fire trekantene. Arealet av de hvite områdene i de to store kvadratene må derfor være like, og dette gir Pytagoras’ setning.
Thomas Heath omtaler dette beviset og et forslag fra de to matematikerne Carl Anton Bretschneider og Hermann Hankel om at dette kan ha vært kjent av pytagoreerne.[8] Heath vil ikke avvise en slik teori, men mener selv at det er mer sannsynlig at pytagoreerne kjente beviset basert på formlike trekanter.
Algebraisk bevis[rediger | rediger kilde]
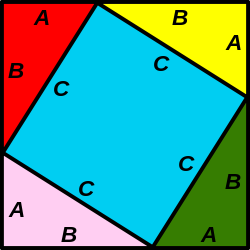
Et algebraisk bevis kan gjennomføres ved å betrakte fire identiske trekanter plassert i hjørnene til et større kvadrat.[11] Beviset er gjengitt av den indiske matematikeren Bhaskara, som levde på 1200-tallet.
Sidelengdene i trekantene er , og , og det store kvadratet har sidelengde .
Arealet av hver av de fire trekantene er gitt ved:
I hver trekant er motstående vinkel til -siden og -siden komplementvinkler. Også det blå området er derfor et kvadrat, med areal lik . Arealet til det store kvadratet med sidelengde er gitt ved
Alternativt kan dette uttrykkes som arealsummen for de fire trekantene og det blå kvadratet:
En sammenstilling av de to uttrykkene for gir Pytagoras’ teorem.
Det omvendte teoremet[rediger | rediger kilde]
Euklid viste i teorem I.48 at også det omvendte Pytagoras’ teorem er gyldig, der en bytter forutsetning og konklusjon:[12]
- «For tre vilkårlige, positive tall a, b og c der a2 + b2 = c2, finnes det en rettvinklet trekant med sider a, b og c. Den rette vinkelen er mellom sidene med lengde a og b.»
Teoremet kan bevises som følger:
La være en trekant med sidelengder , og . Anta også at . Konstruerer en ny rettvinklet trekant , med den rette vinkelen mellom sider med lengde og . Fra Pytagoras’ setning følger det at hypotenusen i trekant har lengde . Trekantene og har tre like sider og er derfor kongruente. Følgelig har de også like vinkler. I trekant må derfor vinkelen mellom sidelengdene and være en rett vinkel.
Pytagoreiske tripler[rediger | rediger kilde]
Utdypende artikkel: Pytagoreisk trippel
Et pytagoreisk trippel består av tre positive heltall , , og , slik at .[13] En vanlig skrivemåte for et slikt trippel er . Et pytagoreiske trippel representerer sidelengdene i en rettvinklet trekant, når alle tre lengdene har heltallsverdier. Eksempler på pytagoreiske tripler er (3,4,5) og (5,12,13).
Dersom er et pytagoreisk trippel, så vil også være det, for et vilkårlig heltall . Dersom de tre tallene , , og ikke har noen felles faktor, så kalles de tre tallene for et primitivt trippel.[1] Tallene er da relativt primiske. Mens (3, 4, 5) er et primitivt trippel, er (6, 8, 10) et trippel med en felles faktor 2.
Pytagoreiske tripler kan brukes til å konstruere rette vinkler og til å kontrollere om en gitt vinkel er rett. Et hendig trippel er (60,80,100), et ikke-primitivt trippel som kan dannes ved å multiplisere tallene i (3,4,5) med 20. En vinkel i et innvendig hjørne i et rom kan kontrolleres ved å avsette henholdsvis 60 cm langs den ene veggen, 80 cm langs den andre. Om nå en meter-lengde passer mellom merkene, så er vinkelen rett.
Konsekvenser og bruk av læresetningen[rediger | rediger kilde]
Inkommensurable lengder og irrasjonale tall[rediger | rediger kilde]
En konsekvens av Pytagoras’ teorem er at det er mulig å konstruere inkommensurable lengder, det vil si lengder med et forhold lik et irrasjonalt tall. Et enkelt eksempel er gitt ved rettvinklet trekant der begge katetene har lengde 1. Pytagoras’ setning gir at hypotenusen i en slik trekant har lengde lik kvadratroten av 2. At dette tallet er et irrasjonalt tall, kan vises ved et enkelt algebraisk bevis, se Kvadratroten av 2.
For greske matematikere var en irrasjonell størrelse definert som et forhold mellom lengder og ikke som et tall. Det skulle gå lang tid før en forståelse av irrasjonale tall skulle bli etablert. Eksistensen av inkommensurable lengder har opphav hos pytagoreerne, men det er ikke kjent nøyaktig når og hvordan kjennskap til slike størrelser ble etablert.[14] Historikeren Proklos, som levde i det femte århundre etter Kristus, gir æren til Pytagoras selv, men ifølge Thomas Heath er det mest sannsynlig at kunnskapen oppstod en god stund etter at Pytagoras var død. En av flere alternative historier om pytagoreeren Hippasos et at han ble druknet, etter å ha røpet kunnskapen om inkommensurable størrelser.[15] Euklid bruker bok X til å diskutere inkommensurable lengder og areal.[16]
Distanse i euklidske rom[rediger | rediger kilde]
Metrikken eller avstandsmålet i euklidsk geometri er basert på Pytagoras’ teorem. Hvis og er kartesiske koordinater til to punkt i planet, så er avstanden mellom disse gitt ved
Dette avstandsmålet kalles euklidsk avstand eller euklidsk metrikk.
I et generelt euklidsk n-dimensjonalt rom er avstanden mellom to vektorer og definert ved
Bruk i kompleks analyse[rediger | rediger kilde]

Et vilkårlig komplekst tall kan skrives på formen
Absoluttverdien eller modulus til dette tallet er definert ved[17]
Sammenhengen mellom de tre størrelsene , og er gitt ved Pytagoras’ ligning:
Absoluttverdien er alltid definert positiv, selv om og kan ha både positive og negative verdier. Geometrisk er avstanden fra origo til i det komplekse planet.
Avstanden mellom to komplekse tall og kan defineres ved
Denne avstanden og de to gitte tallene er igjen relatert ved en ligning tilsvarende Pytagoras’ ligning:
Den pytagoreiske trigonometriske identiteten[rediger | rediger kilde]

For en rettvinklet trekant, som vist nederst i figuren til høyre, kan de trigonometriske funksjonene sinus og cosinus defineres ved
Ved å bruke Pytagoras' teorem, følger det fra disse definisjonene at
Denne grunnleggende identiteten blir kalt enhetsformelen og noen ganger også den pytagoreiske trigonometriske identiteten.[trenger referanse] For to formlike trekanter er forholdet mellom samsvarende sidelengder det samme, og dette vil også gjelde for de to trekantene i figuren. Den øverste rettvinklet trekanten har hypotenusen med lengde 1, og katetene har lengde og .
Generaliseringer[rediger | rediger kilde]
Cosinussetningen[rediger | rediger kilde]

Pytagoras’ teorem er et spesialtilfelle av et mer generelt teorem om forholdet mellom sidelengder i en vilkårlig trekant, kjent som cosinussetningen eller den utvidede pytagoreiske læresetning.[18][19] For en vilkårlig trekant med sidelengder , og er
- .
Her er vinkelen mellom sidene med lengde og . For lik 90 grader er , og ligningen reduserer seg til den vanlige pytagoreiske ligningen.
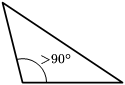
Cosinussetningen gir en enkel metode for å bestemme om en trekant er rett, spissvinklet eller stumpvinklet. Siden cosinus-funksjonen er positiv for en spiss vinkel, men negativ for en stump vinkel, så gjelder følgende:
- hvis og bare hvis trekanten er rettvinklet.
- hvis og bare hvis trekanten er spissvinklet.
- hvis og bare hvis trekanten er stumpvinklet.
Her er forutsatt at er den lengste siden. En vanlig notasjon er å la vinklene i trekanten være , slik at er motstående til sidelengden og motstående til sidelengden . Forholdene over kan da også uttrykkes slik:
- I en spissvinklet trekant er og .
- I en stumpvinklet trekant er og .
Edsger Dijkstra har samlet disse resultatene ved hjelp av fortegnsfunkjonen:[20]
Parallellogramloven[rediger | rediger kilde]

Parallellogramloven er en generalisering av Pytagoras’ sats til et vilkårlig parallellogram, tilskrevet Apollonios fra Perge.[21]
For et rektangel er de to diagonalene like lange: , og parallellogramloven reduserer seg til Pytagoras’ læresetning.
Formlike figurer[rediger | rediger kilde]
Pytagoras’ læresetning kan tolkes som en relasjon mellom arealet til kvadrater på sidekantene. Ved å multiplisere alle tre leddene i Pytagoras’ ligning med , ser en umiddelbart at samme relasjon også gjelder for arealene til halvsirkler med diameter langs sidekantene. Dette resultatet er referert uten bevis av Hippokrates fra Khíos, som levde i det femte århundre før Kristus.[22] Euklid viste i bok VI av Elementer et bevis for a resultatet gjelder for vilkårlige formlike konvekse polygon.[22] I ettertid er det vist at resultatet er gyldig for vilkårlige formlike figurer, også figurer der sider er definerte ved kurver:[trenger referanse]
- «Hvis en reiser formlike figurer på sidene av et rett trekant, så er summen av arealene på de to minste sidene lik arealet av figuren på den største siden.»
De tre sidelengdene i den rette trekanten er lik sidelengder i de tilstøtende figurene, slik at disse må være formlike i forholdet . Den grunnleggende idéen bak generaliseringen er at i formlike figurer er forholdet mellom arealet og kvadratet av en vilkårlig karakteristisk lengde det samme:
 |
 |
Pappos arealteorem[rediger | rediger kilde]
Pappos (3-4. århundre) gir et arealteorem han selv kaller en utviding av Euklid I.47.[23] Dersom en på to sider i en vilkårlig trekant tegner to vilkårlige parallellogram, så kan en konstruere et parallellogram på den tredje siden, slik at arealet av dette er lik summen av arealene til de to første.
 |
Romgeometri[rediger | rediger kilde]

En lengde i det tredimensjonale rommet kan defineres ved gjentatt bruk av Pytagoras’ setning. I figuren til høyre kan en finne lengden av linjestykket ved å bruke den rettvinklede trekanten :
Kateten i denne er gitt ved å bruke Pytagoras’ sats på trekanten :
Kombinasjon av disse to ligningene gir
Resultatet er det tredimensjonale uttrykket for lengden av en vektor , basert på komponentene. Vektoren svarer til diagonalen
de Guas teorem[rediger | rediger kilde]
I tre romdimensjoner er de Guas teorem en generalisering av Pytagoras’ læresetning til et tetraeder:[24]
- «Hvis et tetraeder har et rettvinklet hjørne, så er kvadratet av arealet på den motstående side til den rette vinkel lik summen av kvadratene av arealene på de tre andre sidene.»
Et rettvinklet hjørne er som hjørnet i en kube. Teoremet er navngitt etter Jean Paul de Gua de Malves (1713-1785).
Indreproduktrom[rediger | rediger kilde]
Pytagoras’ sats kan generaliseres til et vilkårlig indreproduktrom, som igjen er en generalisering av det euklidske rommet i to og tre dimensjoner.[25] Et indreproduktrom kan ha både endelig og uendelig dimensjon. Elementene i et indreproduktrom, vektorene, kan for eksempel være funksjoner. I et indreproduktrom kan en definere lengden av elementer, avstanden mellom to elementer og også vinkelen mellom to elementer.
Indreproduktet mellom to elementer og kan betegnes som , og dette generaliserer det vanlige skalarproduktet mellom to endelig-dimensjonale vektorer. To vektorer står ortogonalt på hverandre dersom indreproduktet mellom dem er lik null. Lengden av en vektor er definert ved normen:
I et indreproduktrom sier Pytagoras’ teorem at for to ortogonale vektorer og gjelder at
Vektorene og spiller samme rolle som katetene i en rettvinklet trekant, med hypotenusen gitt som vektorsummen . Teoremet følger av egenskaper til indreproduktet:
Ligningen kan generaliseres til et vilkårlig endelig antall parvis ortogonale vektorer:
Også parallellogramloven kan generaliseres til et vilkårlig indreproduktrom, da med formen
Differensialgeometri[rediger | rediger kilde]
I differensialgeometri blir det for det tredimensjonale euklidske rommet definert en infinitesimal lengde ved[26]
- .
Dette svarer til bruk at Pytagoras’ setning for en infinitesimal avstand mellom to punkt. For en glatt parametrisk kurve gitt på formen
brukes dette til å definere buelengden av kurven:
Ikke-euklidsk geometri[rediger | rediger kilde]
Pytagoras’ setning er basert på aksiomer i euklidsk geometri, og den euklidske formen er ikke gyldig i ikke-euklidsk geometri. I sfærisk geometri vil for eksempel alle tre sidene i en rettvinklet trekant som begrenser en oktant i en enhetskule, ha sidelengder . Dette bryter opplagt med Pytagoras’ ligning.
For ikke-euklidsk geometri kan en utlede alternative former for Pytagoras’ teorem. I sfærisk geometri gjelder det at for enhver rettvinklet sfærisk trekant, på en kule med radius , kan Pytagoras’ teorem skrives som:
Når radien går mot uendelig, vil kuleflaten nærme seg en plan flate. Tilsvarende vil den sfæriske formen på Pytagoras’ teorem gå mot den euklidske formen. Dette kan vises ved å utvikle cosinus-leddene som maclaurinrekker.
I en hyperbolsk geometri med uniform krumning kan Pytagoras’ teorem uttrykkes som:
Ved å rekkeutvikle den hyperbolske funksjonen som en maclaurinrekke, vil (når man tar med de to første leddene) . Det kan da vises at når en hyperbolsk trekant blir lite (altså når a, b og c alle går mot null), vil den hyperbolske formen av teoremet gå mot den euklidske formen.
Historie[rediger | rediger kilde]
Opphavet og historien til Pytagoras’ teorem har gjennom tidene skapt mye diskusjon, og mange teorier er fremsatt. Det kan være vanskelig å skille mellom fakta, tolkninger, grunngitte hypoteser og rene gjetninger. Kanskje har kunnskapen om sammenhengen mellom trekantsidene oppstått på ulike steder til ulike tider, uavhengig av hverandre.
Samtidig har mye kunnskap også blitt utvekslet på tvers av landegrenser og tidsepoker, uten at vi i dag har kjennskap til dette. At en forståelse av teoremet har eksistert svært lenge før Pytagoras levde og virket, er nå allment akseptert.[27][28] Antagelig har forståelsen for teoremet vokst fram gjennom ulike stadier: en oppfatning av en rett vinkel, kunnskap om pytagoreiske tripler, kjennskap til sammenhengen mellom sidene i en rettvinklet trekant, kjennskap til sammenhengen mellom trekantvinkler og endelig teoremets bevis.
Det er verdt å være oppmerksom på at bruk av begrep som «Pytagoras’ teorem» og «bevis» i forbindelse med oldtidens matematikk lett kan skape feil inntrykk. Et utsagn som «xxx hadde et bevis for Pytagoras teorem tusen år før Pytagoras» kan som regel møtes med mange spørsmål, både når det gjelder kildebruk, tidsbestemmelse, formen på «teoremet» og kvaliteten av «beviset».
I forhistorisk matematikk[rediger | rediger kilde]
Oppmåling av europeiske og egyptiske megalittiske monumenter fra ca. 2500 år f.Kr. har ført til at det er framsatt teorier om at steinene i disse monumentene er plassert i former basert på rettvinklede trekanter med heltalssider.[29] Den nederlandske matematikeren Bartel Leendert van der Waerden gjetter på at de involverte pytagoreiske triplene ble funnet algebraisk.[30]
I babylonsk matematikk[rediger | rediger kilde]
Utdypende artikkel: Babylonsk matematikk

Funn av steintavler fra viser at babylonerne var godt fortrolige med ulike former for algebra, inkludert beregning av pytagoreiske tripler.[31] Det har vært spekulert i hva babylonerne brukte de pytagoreiske triplene til, og en mulighet kan ha vært i løsning av systemer av andregradsligninger med to ukjente. Babylonerne var også kjent med sammenhengen mellom en rettvinklet trekant og pytagoreiske tripler.
En svært viktig kilde til kunnskap er kileskrifttavlen Plimpton 322 fra Mesopotamia, skrevet i perioden 1822-1784 f.Kr.[31] Den antas å stamme fra den babylonske byen Larsa. Tavlen inneholder en tabell med fire kolonner og 15 rader. Kolonne nummer fire fra venstre nummererer radene, med tall fra 1 til 15. Kolonne nummer en er delvis ødelagt. Kolonne nummer to og tre har som overskrift henholdsvis «Bredde» og «Diagonal». Tabellen er tolket som å inneholde tall brukt for å konstruere pytagoreiske tripler, inkludert de følgende:
- .
En slik tolkning viser at babylonerne hadde metoder til å regne ut triplene, og tallene i tavlen kan indikere at de kjente Diofants konstruksjonsmåte.
En annen tavle i kileskrift, fra Hammurabi-dynastiet (1829–1530 f.Kr.), finnes nå i British Museum.[32] Tavlen inneholder et geometrisk problem, med løsning gitt i det seksagesimale tallsystem:[33][34]

| Originalteksten i oversettelse | Kommentarer |
| En stav: 0;30 GAR | 30/60 GAR = 1/2 GAR ≈ 3 m lang.[35] |
| foroven er den sunket 0;6 | Når toppen er senket 6/60 |
| nedentil har den fjernet seg | ..hvor langt har foten fjernet seg fra vertikalen? |
| 0;30 kvadrere: 0;15, skjønner? | (30/60)2 = 900/3500 = 15/60 |
| trekke 0;6 fra 0;30: 0;24, skjønner? | -6/60 + 30/60 = 24/60 |
| 0;24 kvadrere: 0;9,36, skjønner? | (24/60)2 = 576/3600 = 0;9,36 |
| trekk 0;9,36 fra 0;15: 0;5,24, skjønner? | - 576/3600 + 15/60 = 324/3600 = 0;5,24 |
| 0;5,24 har kvadratroten? 0;18 | (324/3600)−2 = 18/60 = 0;18 |
| 0;18 GAR har den fjernet seg ved bakken |
Løsningen i tavlen kan skrives som:
Dette svarer til Pytagoras’ sats på formen . Fra denne kilden fremgår imidlertid ikke om babylonerne kjente noe matematisk bevis.
Ifølge historikeren Jamblikos skal Pytagoras ha oppholdt seg tolv år i Babylon.[36]
I egyptisk matematikk[rediger | rediger kilde]
Utdypende artikkel: Oldtidens egyptiske matematikk
En vanlig oppfatning er at egyptisk matematikk ikke nådde like langt som den babylonske, spesielt ikke innenfor algebra.[37][38] Om de utviklet ny geometrisk kunnskap er omdiskutert.[38] Gjennom landmåling la imidlertid egypterne et grunnlag for den etterfølgende greske geometrien, og egypterne har brukt pytagoreiske tripler til hjelp for å konstruere rette vinkler. En tau-ring med tolv ekvidistante knuter kan brukes til å danne en trekant med sidene 3,4,5, og derved danne en rett vinkel.
Det er lite funn av direkte kilder om egyptisk kjennskap til den pytagoreiske læresetningen. Verken Moskva-papyrusen eller Rhind-papyrusen nevner problemstillinger der denne er i bruk. Berlin-papyrus 6619 er skrevet mellom 2000 og 1786 f.Kr. i Mellomriket, og her forekommer fire ligninger som alle er basert på det pytagoreiske trippelet (3,4,5):[39]
Papyrusen inneholdet imidlertid ingen referanse til trekanter.
Mye av kunnskapen om egyptisk geometri kommer fra greske kilder.[40] Den antikke historikeren Herodot forteller om egyptisk landmåling og gir dette æren for opphavet til geometri. Proklos forteller at grekeren Tales fra Milet reiste til Egypt og lærte geometri der. Også Pytagoras skal ha vært på reise i Egypt.[36] Demokrit skryter av at ingen har overgått ham i geometrisk kunnskap, ikke en gang de egyptiske «tau-strekkerne».[40]
I indisk matematikk[rediger | rediger kilde]
Utdypende artikkel: Indisk matematikk

Śulbasūtraene er en samling av indiske sutra-tekster fra engang mellom det 8. og 2. århundre f.Kr. Dette verket er en del av en større samling av religiøse tekster, og delen omtaler matematikk for å kunne konstruere brennalter og for å sette opp en kalender over religiøse høytider[41] Tittelen kan oversettes med «Regler for bruk av snoren».[42] Teksten lister fem pytagoreiske tripler, gir en form for Pytagoras’ teorem og viser i tillegg at teoremet er gyldig for en likesidet trekant.[43][44][45]
Der eksisterer minst fire versjoner av Sulbasutraene, men geometri-beskrivelsen er relativt like i disse fire.[46] Versjonen som skal være laget av Baudhayana er anslått å være fra omkring 600 f.Kr., det vil si rundt hundre år før Pytagoras. Mye tyder på at kunnskapen som er samlet i teksten kan være betydelig eldre. Baudhayana-Sulbasutra drøfter flere problem der oppgaven er å konstruere en figur med samme areal som en eller flere andre figurer. I Sutra 50 gir teksten en oppskrift for å summere arealet av to kvadrat, illustrert ved figuren til høyre:
Hvis du vil slå sammen to ulike kvadrater til ett, ta det største kvadratet og legg til et bit av det største. Biten skal være laget med en side lik siden i det minste kvadratet. Diagonalen i denne biten er siden i det kombinerte kvadratet.
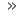 Baudhayana Sutra 50[46]
Baudhayana Sutra 50[46]
Sutra 50, 51 og 54 gir sammen en form for godtgjøring for at Pytagoras’ sats er riktig. Om dette kan gjelde som et generelt «bevis» er omdiskutert.[46][8]
Det er blitt foreslått at inderne hentet kunnskap fra Mesopotamia,[47] men også motsatt, at Mesopotamia fikk kunnskap fra India.[46]
I kinesisk matematikk[rediger | rediger kilde]
Utdypende artikkel: Kinesisk matematikk
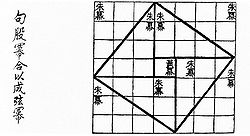
Også kinesisk matematikk har i lang tid kjent til former for Pytagoras’ teorem. Den eldste kjente kinesiske matematiske teksten er antagelig Zhoubi suanjing (Soluret og himmelens sirkler).[48] Tidfestingen av gamle kinesiske matematiske verk er svært usikker, og datering varierer sterkt i ulike kilder. Historien til Zhoubi suanjing kan gå helt tilbake til 1200 f.Kr, men verket har kanskje fått en endelig form en gang mellom 500 f.Kr. og 200 e.Kr. Innholdet er astronomiske beregninger, men også geometri for trekanter og litt om brøkregning. I likhet med både babylonske, indisk og egyptiske tekster, er dette en samling av problemer, med løsning. Blant de 246 problemene som er med i verket, inngår en figur som viser at kineserne kjente til den pytagoreiske læresetningen, med en trekant med sidelengder 3, 4 og 5.[44][49] Figuren er gjengitt til høyre. Den vertikale teksten til venstre for figuren er som følger:
- 勾股幂合以成弦幂
- gōu gǔ mì hé yǐ chéng xián mì
Summen av lengdene til kvadratene til høyden og basen er lik lengden til hypotenusen.
 Soluret og himmelens sirkler[trenger referanse]
Soluret og himmelens sirkler[trenger referanse]
Nesten like gammelt som Zhoubi suanjing, og kanskje vel så innflytelsesrikt, er verket Chiu chang suan shu («Ni kapitler om den matematiske kunst»).[48][49] Også dette er en problem-samling, med løsning på 263 matematiske problemer. I det niende og siste kapittelet omtales pytagoreiske tripler og rette trekanter.[50] Et klassisk problem, som en også finner i indiske tekster, er «problemet med den brukne bambusen»:[49] Et bambustre som er 10 lengder høyt, knekker. Toppen når da bakken 3 lengder fra foten av stammen. Hvor høyt oppe er bambusen brukket? Løsningen krever bruk av Pytagoras’ sats. Hvis er høyden til fra foten til knekkpunktet, så er
En kommentar til Chiu chang suan shu, med tittel Jiuchang suan shu, ble skrevet av Liu Hui i året 263 e.Kr. Her blir det gitt et bevis[bør utdypes] i kapittel 9.[51]
Den pytagoreiske læresetningen var kjent i Kina under navnet Gōugŭ (勾股), «base og høyde». For en trekant med sidene 3, 4 og 5 ble læresetningen kalt Gōugŭ-teoremet (勾股定理, Gōugŭ Dìnglĭ).[trenger referanse]
Pytagoras’ rolle[rediger | rediger kilde]
Utdypende artikkel: Pytagoras

Svært lite håndfast er kjent om personen Pytagoras. Det er ikke funnet noe skriftlig verken fra ham eller fra miljøet rundt ham, og all kunnskap kommer fra senere omtale. Nøyaktig leveår for Pytagoras er ikke kjent, men det er antatt at han levde i perioden 580-475 f.Kr.[52] Beretninger om Pytagoras reiser til Babylonia og Egypt, fortalt av blant annet Jamblikos, har i ettertiden blitt møtt med både tillit og skepsis, men det er grunn til å tro at de inneholder en kjerne av sannhet.[36][53] Pytagoras ble leder for et filosofisk, matematisk og religiøst brorskap i Kroton, kjent som pytagoreerne.
Hvor mye kunnskap pytagoreerne hadde om sammenhengen mellom sidene i en rettvinklet trekant, er ikke kjent. Både Pytagoras og senere følgesvenner var nok fortrolige med pytagoreiske tripler, og etter tradisjonen skal kjennskapen til (3,4,5) ha kommet fra Egypt.[54] Om de hadde et bevis for sammenhengen mellom sidelengdene i en trekant, er omdiskutert. Thomas Heath gir flere bevis som kan ha vært brukt av pytagoreerne. Det er heller ikke kjent hva som ga støtet til kunnskapen om inkommensurable størrelser. Muligens kom dette fra arbeid med pentagramet, som var viktig for pytagoreerne, men det er også naturlig å anta at en likesidet trekant har vært involvert.
En tidlig kilde som tilegner teoremet til Pytagoras, skal ha vært en Apollodoros Arithmetikos, og han blir sitert av flere senere kilder.[8] Detaljer om Apollodoros liv er ikke kjent. Verset som blir sitert etter Apollodoros er heller ikke entydig:
Da Pytagoras, som første, den berømte tegningen fant,
han brakte da som offer et guddommelig oksedyr.
Apollodoros sier ingenting om hvilken «berømt tegning» han viser til. Det greske ordet brukt om «tegning» kan også tolkes som «teorem».[8] Fortellinger om dyreoffer som takk for kunnskap var også tidligere blitt knyttet til andre, inkludert til Tales. Diogenes Laertios (3. århundre f.Kr.) og flere andre går ut fra at verset gjelder oppdagelsen av Pytagoras’ sats. Romeren Cicero (106-43 f.Kr.) bruker fortellingen om Pytagoras og dyreofferet, uten å spesifisere hvilken geometrisk oppdagelse det gjaldt. Han er imidlertid skeptisk, fordi dyreoffer ikke var godtatt blant pytagoreerne. En annen romer, Vitruvius (ca. 80-ca.15 f.Kr.), knytter fortellingen til oppdagelsen av det pytagoreiske trippelet (3,4,5). Plutark (45-120) var kritisk til å tolke verset i tilknytning til Pytagoras’ teorem. Trass denne uenigheten, var det mange som i ettertid ga Pytagoras æren for å ha oppdaget teoremet.[8] Proklos i det femte århundre etter Kristus stadfester dette, uten selv å ta stilling til sannhetsinnholdet. Ifølge Proklos bør Euklid bli gitt største æren, for han var den ga bevis for teoremet.
I sitt store verk om historien til gresk matematikk, sier Thomas Heath i avsnittet om Pytagoras’ teorem:
Though this is the proposition universally associated with the name of Pythagoras, no really trustworthy evidence exists that it was actually discovered by him.
...
I would not go so far as to deny to Pythagoras the credit of the discovery of our proposition; nay, I like to believe that the tradition is right, and that it was really his. Thomas Heath[8]
Thomas Heath[8]
I ettertiden har det vært stor uenighet om Pytagoras’ rolle, og flere hypoteser er gjeldende:
- Pytagoras overtok satsen fra babylonerne. Han var kun en formidler av orientalsk kunnskap til grekerne. Dette er synet til vitenskapshistorikeren Walter Burkert.[55]
- Pytagoras oppdaget og beviste satsen uavhengig av orientalsk matematikk. Dette var en vanlig oppfatning i antikken og er også synet til vitenskapshistorikeren Leonid Zhmud.[56][57]
- Pytagoras støttet seg til orientalske kilder, men var den første som fant et bevis. Egypterne og babylonerne var primært interessert i satsens anvendelse og ikke i et generelt bevis.
- Pytagoras hadde selv få eller ingen bidrag. Andre pytagoreere kan på et senere tidspunkt ha funnet et bevis og så har dette blitt knyttet til Pytagoras.
Oppfatningen til Thomas Heath ligger kanskje et sted mellom de to siste hypotesene.
Euklids rolle[rediger | rediger kilde]
Utdypende artikkel: Evklid
Euklid hadde mesteparten av sitt virke i Alexandria, omkring 300 f.Kr. Beviset som Euklid bruker for Pytagoras’ teorem i I.47 er antagelig hans eget.[58] Det betyr ikke at det ikke eksisterte eldre bevis eller at Euklid ikke kjente til disse. Euklid bygger opp Elementer svært systematisk, og beviser satsene steg for steg. Beviset for I.47 ble antagelig valgt fordi det ikke trengte bruk av formlike figurer og forhold mellom lengder. Dette emnet ble først introdusert i bok V. Pytagoras’ teorem og det omvendte teoremet avslutter bok I, som høydepunkt. Så om beviset for I.47 i dag kan synes unødig komplisert, så er Euklids fortjeneste at han greidde å gjennomføre dette kun basert på innholdet i bok I.
Euklids Elementer ble antagelig skrevet som en lærebok og ikke som et forsøk på å samle all kjent geometrisk kunnskap eller presentere ny kunnskap.[59] Ingenting blir nevnt om opphavet til innholdet, og heller ikke Pytagoras er nevnt. Det er antatt at store deler av innholdet i bok I, II, IV og VI var kjent for pytagoreerne.[60] Euklid gjør ingen krav på originalitet, men han har antagelig laget nye bevis der dette har vært nødvendig for sammenhengen.[59] Det store bidraget til Euklid var den systematiske oppbyggingen av teorien, der alt blir stringent bevist.
In rectangulis triangulisquadratum, quod a latere rectum angulum subtendentedescribitur, aequale est eis, quae a lateribus rectumangulum continentibus describuntur.
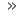 Euklid I.47 i latinsk versjon[54]
Euklid I.47 i latinsk versjon[54]
I rettvinklede trekanter er kvadratet på siden motstående til den rette vinkelen lik kvadratene på sidene som avgrenser den rette vinkelen
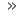 Euklid I.47 i norsk omsetting etter T. Heath[61]
Euklid I.47 i norsk omsetting etter T. Heath[61]
I kulturen[rediger | rediger kilde]
Pytagoras’ læresetning er gjennom tidene referert til eller gjengitt i en lang rekke sammenhenger:
- Et vers i «Generalmajorens sang» i musikalen The Pirates of Penzance av Gilbert og Sullivan har referansen: «About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse.»
- Fugleskremselet Scarecrow i Trollmannen fra Oz gir en referanse til teoremet idet han mottar eksamensbevis fra trollmannen. Han fremviser umiddelbart sin «kunnskap» ved å gjengi en radbrukket og ukorrekt versjon av teoremet: «Summen av kvadratroten på to tilfeldige sider av en likesidet trekant er lik kvadratroten av den siste siden. Oh, hurra! Jeg har vel en hjerne!»
- I en episode av The Simpsons, etter å ha funnet Henry Kissingers briller på toalettet i Springfield Nuclear Power Plant, tar Homer dem på og gjengir Oz Scarecrows forenklede versjon av teoremet. En mann i nærheten roper ut: «Det er en rettvinklet trekant – din idiot!»
- I talesynteseprogramvaren i Mac OS X finnes en stemme kalt Ralph, som gjengir teoremet i en eksempeltekst.
- For en Past Master bruker frimuerereet symbol som er et diagram Euklid brukte i sitt bevis av teoremet.
- I Neal Stephensons spekulative fiction Anathem er Pytagoras’ teorem gjengitt som the Adrakhonic theorem. Et geometrisk bevis er gjengitt på et romskip, for å vise eiernes kunnskap om matematikk.
- I den engelske versjonen av den syttende boken om Asterix, The Mansions of the Gods, benytter Julius Cæsar seg av tjenesten til arkitekten Squareonthehypotenus (Kvadratetpåhypotenusen).
- I 2000 utga Uganda en mynt med form som en rett trekant. Myntens bakside har en illustrasjon av Pytagoras og Pytagoras’ teorem, sammen med teksten «Pythagoras Millennium».[62]
- Hellas, Japan, San Marino, Sierra Leone og Surinam er alle land som har gitt ut frimerker med motiver av Pytagoras og Pytagoras’ teorem.[63]
Historien om dyreofferet til Pytagoras har inspirert dikteren Adelbert von Chamisso til en sonett, Vom pythagoreischen Lehrsatz, der første vers lyder:[trenger referanse]
Die Wahrheit, sie besteht in Ewigkeit,
Wenn erst die blöde Welt ihr Licht erkannt;
Der Lehrsatz nach Pythagoras benannt
Gilt heute, wie er galt zu seiner Zeit.
Oversatt til norsk kan det gjengis slik:
Evighet er Sannhetens byggekloss,
At verden så lyset, er hva det krevde;
Den læresetningen Pytagoras ga oss
Gjelder like mye i dag som da han levde.
Referanser[rediger | rediger kilde]
- ^ a b Judith D. Sally, Paul Sally (2007). Roots to research: A vertical development of mathematical problems (engelsk). American Mathematical Society Bookstore. s. 63ff. ISBN 978-0-8218-4403-8.
- ^ E.S. Loomis: The Pythagorean proposition s.1
- ^ a b C.B.Boyer: A history of mathematics s.119
- ^ «Euclid Elements. Book I, Proposition 47» (engelsk). Perseus Digital Library. Besøkt 12. mars 2021.
- ^ E.S. Loomis: The Pythagorean proposition s.120
- ^ David Eugene Smith (1925). History of mathematics (engelsk). II. Ginn and Company. s. 284.
- ^ E.S. Loomis: The Pythagorean proposition s.24
- ^ a b c d e f g T. Heath A history of Greek mathematics (Vol. I) s.144-149
- ^ «Pythagorean theorem» (engelsk). Angie Head, University of Georgia. Besøkt 12. mars 2021.
- ^ «Mathematical Treasure: James A. Garfield's Proof of the Pythagorean Theorem» (engelsk). Mathematical Association of America. Besøkt 12. mars 2021.
- ^ «Pythagorean theorem. Proof 4» (engelsk). Cut the Knot. Besøkt 13. mars 2021.
- ^ «Euclid Elements. Book I, Proposition 48» (engelsk). Perseus Digital Library. Besøkt 12. mars 2021.
- ^ G.H. Hardy, E.W. Wright (2008). An introduction to the theory of numbers. Oxford: Oxford University Press. s. 245-247. ISBN 978-0-19-921985-8.
- ^ T. Heath A history of Greek mathematics (Vol. I) s.154-157
- ^ T. Heath A history of Greek mathematics (Vol. I) s.65
- ^ T. Heath A history of Greek mathematics (Vol. I) s.402ff
- ^ R.V Churchill, J.W. Brown, R.F. Verhey (1974). Complex variables and applications. Tokyo: McGraw-Hill Kogakusha. s. 7. ISBN 0-07-010855-2.
- ^ Ernest Julius Wilczynski, Herbert Ellsworth Slaught (1914). Plane trigonometry and applications. Allyn and Bacon. s. 85ff.
- ^ Matematikk for den videregående skole. Oslo: Gyldendal. 1986. s. 25. ISBN 82-05-16032-5.
- ^ «On the theorem of Phytagoras» (PDF). Edsger Dijkstra, University of Texas. Besøkt 13. mars 2021.
- ^ A. Holme: Matematikkens historie (Bind 1) s.309
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.397
- ^ T. Heath A history of Greek mathematics (Vol. II) s.369-371
- ^ «De Gua's theorem». Wolfram MathWorld. Besøkt 14. mars 2021.
- ^ Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
- ^ D.J. Struik (1961). Lectures on classical differential geometry. New York: Dover Publications. s. 5-10. ISBN 0-486-65609-8.
- ^ A. Holme: Matematikkens historie (Bind 1) s.26
- ^ «Pythagoras: Everyone knows his famous theorem, but not who discovered it 1000 years before him». Journal of Targeting, Measurement and Analysis for Marketing. 3 (engelsk). 17: 229–242. 1. september 2009. ISSN 1479-1862. doi:10.1057/jt.2009.16. Besøkt 5. oktober 2023.
- ^ «Megalithic monuments». Arkivert fra originalen 6. juli 2011. Besøkt 17. januar 2010.
- ^ B.L. van der Waerden: Geometry and algebra ... s.??
- ^ a b A. Holme: Matematikkens historie (Bind 1) s.21ff
- ^ «Tablet 85196». British Museum. Besøkt 14. mars 2021.
- ^ H. Geriche: Mathematik in Antike und Orient s.33f
- ^ K. Vogel: Vorgriechische Mathematik s.67f
- ^ K. Vogel: Vorgriechische Mathematik s.20
- ^ a b c A. Holme: Matematikkens historie (Bind 1) s.169
- ^ A. Holme: Matematikkens historie (Bind 1) s.59ff
- ^ a b C.B.Boyer: A history of mathematics s.40
- ^ Stephen Hawking (2005). God created the integers: The mathematical breakthroughs that changed history. Greenworld Books. ISBN 978-0762419227.
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.123ff
- ^ Swami Vishnu (2018). Vedic science & history. Gosai Publishers. s. 65f. ISBN 978-8-1926601-3-4.
- ^ A. Holme: Matematikkens historie (Bind 1) s.122
- ^ H. Geriche: Mathematik in Antike und Orient s.68
- ^ a b Oskar Becker (1966). Das mathematische Denken der Antike. Göttingen: Vandenhoeck & Ruprecht. s. 55f.
- ^ Euclid: The thirteen books of... s.360-364
- ^ a b c d David W. Henderson, Daina Tamina. Experiencing geometry. Project Euclid. s. 174ff. ISBN 978-0131437487.
- ^ C.B.Boyer: A history of mathematics s.229
- ^ a b C.B.Boyer: A history of mathematics s.217
- ^ a b c A. Holme: Matematikkens historie (Bind 1) s.87
- ^ F. Swetz, T.I. Kao: Was Pythagoras Chinese? ... s.??
- ^ Karine Chemla, Guo Shuchun (2005). Les neuf chapitres. Le classique de la Chine ancienne et ses commentaires. Édition critique. Dunod. s. 680. ISBN 978-2100495894.
- ^ A. Holme: Matematikkens historie (Bind 1) s.164
- ^ A. Holme: Matematikkens historie (Bind 1) s.178f
- ^ a b E.S. Loomis: The Pythagorean proposition s.4
- ^ Walter Burkert (1962). Weisheit und Wissenschaft. Nürnberg. s. 405f, 441ff.
- ^ Leonid Zhmud (1997). Wissenschaft, Philosophie und Religion im frühen Pythagoreismus. Berlin. s. 141-151, 160-163.
- ^ Euclid: The thirteen books of... s.350-360
- ^ T. Heath A history of Greek mathematics (Vol. I) s.378
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.354ff
- ^ T. Heath A history of Greek mathematics (Vol. I) s.201
- ^ A. Holme: Matematikkens historie (Bind 1) s.264
- ^ «Le Saviez-vous ?». Arkivert fra originalen 21. september 2009.
- ^ Miller, Jeff (3. august 2007). «Images of mathematicians on postage stamps». Besøkt 6. august 2007.
Litteratur[rediger | rediger kilde]
På norsk:
- Holme, Audun (2008). Matematikkens historie. 1. Bergen: Fagbokforlaget. ISBN 978-82-450-0697-1.
På engelsk:
- Boyer, Carl B. (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
- Euclid (1956). The thirteen books of the Elements. Translated with an introduction and commentary by Sir Thomas L. Heath. I, II og III. Dover. ISBN 978-0-486-60088-8.
- Heath, Thomas (1981). A history of Greek mathematics. I og II. New York: Dover Publications. ISBN 0-486-24073-8.
- Loomis, Elisha Scott (1968). The Pythagorean proposition (PDF). Washington, D.C: The National Council of Teachers of Mathematics. ISBN 978-0873530361.
- Maor, Eli (2007). The Pythagorean theorem: A 4,000-Year History. =Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Stillwell, John (1989). Mathematics and its history. Springer-Verlag. ISBN 3-540-96981-0.
- Swetz, Frank, Kao, T. I. (1977). Was Pythagoras Chinese? An examination of right triangle theory in ancient China. Pennsylvania State University Press.
- van der Waerden, B.L. (1983). Geometry and algebra in ancient civilizations. Springer. ISBN 978-0387121598.
På tysk:
- Fraedrich, Anna M. (1994). Die Satzgruppe des Pythagoras. Heidelberg: Spektrum Akademischer Verlag. ISBN 3-86025-669-6.
- Gericke, Helmuth (1984). Mathematik in Antike und Orient. Berlin: Springer. ISBN 978-3-642-68630-6.
- Vogel, Kurt (1959). Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier. Hannover: Hermann Schroedel.
Eksterne lenker[rediger | rediger kilde]
- (en) Pythagorean theorem – kategori av bilder, video eller lyd på Commons
- «Pythagorean Theorem» (engelsk). Cut the Knot. Besøkt 15. mars 2021. Mer enn 70 bevis
- «Pythagoras's Theorem in Babylonian Mathematics» (engelsk). MacTutor. Besøkt 15. mars 2021.
- «Pythagorean Theorem» (engelsk). Wolfram MathWorld. Besøkt 15. mars 2021.
- «Euclid's Elements» (engelsk). Clark University, USA. Besøkt 15. mars 2021.



























































![{\displaystyle {\begin{alignedat}{2}{\frac {(a+b)^{2}}{2}}\ &=\ ab+{\frac {c^{2}}{2}}\\[5pt]a^{2}+2ab+b^{2}\ &=\ 2ab+c^{2}\\[5pt]a^{2}+b^{2}\ &=\ c^{2}.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53c9d6e9f45e0666c18df9e1b831ae19813fad89)

















































![{\displaystyle {\begin{alignedat}{2}&{\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\\[7pt]&\Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C=C\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c57c9fedc6ac7e6528510a2309ef2899db16f59a)

















![{\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} \qquad t\in [a,b]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b241899d3a43740404e9505d6d5069ab22008dc)











