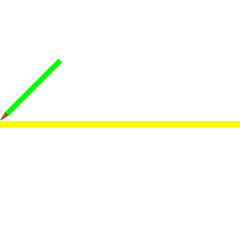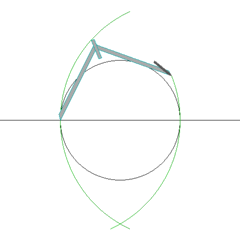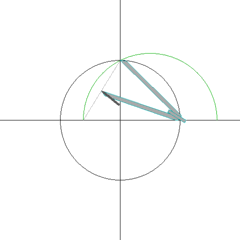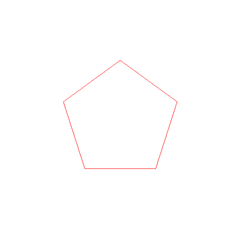
Regulær mangekant

En regulær polygon eller regulær mangekant er innen euklidsk geometri en polygon som er både likesidet og likevinklet, det vil si at alle sidekantene er like lange og alle vinklene er like store. Mangekanten fremkommer ved å forbinde punktene med rette linjestykker. Forbindes hvert punkt på sirkelen med sine nabopunkt fremkommer de mest vanlige, regulære mangekantene som for eksempel pentagon og heksagon. Disse er konvekse og har den egenskapen at hver linje som skjærer en side, vil skjære kun en annen side. Regulære polygoner kan også være stjerneformede. Det finnes et uendelig antall regulære polygoner, og konvekse regulære mangekanter navnsettes med antallet kanter de har enten på norsk eller på gresk etterfulgt av -kant på norsk eller -gon på gresk. I en matematisk følge av konvekse regulære polytoper vil grenseverdien være en sirkel.
Punktene på sirkelen er mangekantens hjørner eller vertex, mens linjestykkene som forbinder punktene er mangekantens sider. Da den er regulær, har alle sidene samme lengde. Det er like mange sider som hjørner i en slik polygon. Sirkelen med hjørnene omskriver mangekanten. Man kan også innskrive en sirkel i mangekanten slik at den tangerer alle dens sider. Regulære mangekanter er sykliske polygoner.

Forbindes derimot hvert punkt på sirkelen med nest nærmeste eller tredje nærmeste nabo, vil en regulær stjernepolygon fremstå. Disse er ikke lenger konvekse. De mest kjente eksemplene er pentagram og heksagram. I disse mangekantene vil sidene krysse hverandre, og de er derfor ikke enkle.
Regulære mangekanter har vært kjente i lang tid tilbake. Deres egenskaper ble studert av greske matematikere i antikkens Hellas. Arkimedes benyttet regulære mangekanter til å gi et numerisk svar på spørsmålet om sirkelens kvadratur. Hans mest nøyaktige verdi for konstanten π var basert på innskrevne og omskrevne 96-kanter.
Overflaten til de platonske legemene er dannet av regulære trekanter, firkanter og femkanter. Alle disse lar seg konstruere ved hjelp av linjal og passer. Ved å halvere hver sidekant i disse fremkommer regulære 6-kanter, 8-kanter og 10-kanter. I 1796 viste Gauss at også den regulære 17-kanten kunne konstrueres.
Omkrets og areal[rediger | rediger kilde]


Hver side i en konveks, regulær mangekant med n hjørner vil utspenne en vinkel α = 360°/n sett fra den omskrevne sirkels sentrum. Dette er mangekantens sentralvinkel. Da summen av vinklene i en trekant er 180°, vil den indre vinkelen i mangekanten være β = 180° - α = (1 - 2/n)⋅180°. Den nærmer seg 180° når antall sidekanter blir veldig stort. Den ytre vinkelen γ = 180° - β = α er lik sentralvinkelen og vil derimot gå mot null i samme grense.
Uttrykt ved radianer er sentralvinkelen α = 2π/n. Hvis R er radius i den omskrevne sirkelen, så er lengden av en side i mangekanten lik med s = 2R sinα/2 eller
Radius i den innskrevne sirkelen er på samme måte
Historisk blir denne avstanden fra mangekantens sentrum til en side kalt for dens apotema.
Summen av alle sidene i mangekanten gir dens omkrets eller perimeter p = ns. Settes her inn for sidekanten s, er den
Når antall sider n blir veldig stort, går denne mot verdien 2π R som for en sirkel. Det følger fra at (sinx)/x = 1 når x → 0.
Areal[rediger | rediger kilde]
Hver trekant med en sidekant som grunnlinje og toppunkt i mangekantens sentrum har areal as/2. Settes her inn for sidekanten s og apotema a og multipliseres dette med n, fås arealet til hele mangekanten,
Dette går mot π R2 når antall sider n blir veldig stort. I den grensen går den regulære mangekanten over til å bli en sirkel.
Geometrisk konstruksjon[rediger | rediger kilde]
Fra en vilkårlig n-kant kan man konstruere en 2n-kant ved å halvere alle sidekantene. Den enkleste og minste, regulære mangekanten er tokanten eller en digon. I euklidsk geometri er denne degenerert til en rett linje som er en diameter i den omskrevne sirkelen. Ved å halvere de to degenererte sidene oppstår en regulær firkant som er et kvadrat. Ved videre halveringer kan man konstruere 8-kanter eller oktagoner, 16-kanter og så videre. Fra den regulære trekanten kan man konstruere en 6-kant og videre 12-kanter, 24-kanter og så videre. Og fra 5-kanten fremkommer 10-kanter, 20-kanter og så videre ved slike sidehalveringer.
Hvis man kan konstruere en p-kant med sentralvinkel 2π/p og en q-kant med sentralvinkel 2π/q hvor tallene p og q er relativ primiske, kan man også konstruere en pq-kant ved å la p-kanten og q-kanten ha et felles hjørne på samme sirkel. Det skyldes at slike primtall oppfyller ap + bq = 1 for visse heltall a og b slik at 2aπ/q + 2bπ/p = 2π/pq som er sentralvinkelen i pq-kanten. Dette gjør det mulig å konstruere en 15-kant fra en 3-kant og en 5-kant. Dermed kan man også konstruere 30-kanter, 60-kanter og så videre. Derimot går det ikke an å konstruere en regulær 9-kant da 3 ikke er relativt primisk til 3.
Alt dette var kjent for de greske matematikere i antikkens Hellas. Denne kunnskapen kan oppsummeres i formelen
hvor m = 0,1,2,3,... og νi = 0,1. Den gir antall sider til de regulære mangekantene som man mente kunne konstrueres med passer og linjal.
Dette var situasjonen frem til 1796 da Carl Friedrich Gauss som 19-årig student ved Universitetet i Göttingen viste at den regulære 17-kanten kunne lages ved en slik geometrisk konstruksjon. Noen år senere publiserte han den matematiske forklaringen og viste at også regulære mangekanter med n = 257 og 65537 sider kan konstrueres. Antall sider i en regulær mangekant med et odde antall sider måtte være lik med et Fermat-tall eller et produkt av forskjellige slike. Dette resultatet kan sammenfattes i formelen
hvor m igjen er et heltall, Fi står for Fermat-tallene 3,5,17,257,65537 og νi = 0,1. De fem Fermat-tallene gir derfor opphav til i alt 31 regulære, konstruerbare mangekanter med et odde antall sider.
Omtrent tredve år senere viste Pierre Wantzel hvordan disse resultatene passet inn i en større sammenheng basert på utvidelser av tallkropper. Dette var igjen en videreføring av hva Niels Henrik Abel hadde kommet frem til om løsbarheten av polynomligninger. På den måten ble det klart at en geometrisk konstruksjon av et tall kun er mulig når dette inneholder rasjonelle uttrykk som i alminnelighet involverer kvadratrøtter av rasjonelle uttrykk med kvadratrøtter som igjen inneholder kvadratrøtter og så videre et endelig antall ganger. For å konstruere en n-kant må derfor sentralvinkelen 2π/n kunne konstrueres og dermed tallet cos2π/n. Man kan for eksempel konstruere en 120-kant med en sentralvinkel på 3°. Da 120 = 23⋅3⋅5, kan det gjøres ved å starte med en 15-kant og så halvere sidekantene tre ganger. Det tilsvarer den eksakte verdien
som er et konstruerbart tall da det inneholder kun kvadratrøtter og en kvadratrot av en kvadratrot.
Sirkeldelingsligningen[rediger | rediger kilde]

Konstruksjon av en regulær n-kant er ekvivalent med å finne løsningene eller røttene til den spesielle polynomligningen
Den har opplagt løsningen x = 1. Men hvis man også tillater komplekse røtter, så kan alle skrives som
hvor k = 0,1,2,..., n-1 og i = √-1 er den imaginære enheten. Den reelle løsningen x = 1 tilsvarer z0 = zn = 1. Disse n røttene ligger på en sirkel i det komplekse planet og danner hjørnene i en mangekant med n sider og sentralvinkel αn = 2π/n.
For n = 2 er begge løsningene x = ± 1 reelle, og mangekanten er en 2-kant som består av en diameter i sirkelen. Mer interessant er den likesidete trekanten som kommer frem for n = 3. De tre røttene er da
mens for n = 4 blir røttene (±1, ±i) og danner et kvadrat. Når n = 5, fremkommer en pentagon som figuren viser.
Produktet av to røtter er en ny rot. På samme måte gir potensen av en rot, i alminnelighet en annen rot. Tar man alle potenser av en og samme rot zk, vil resultatet enten bli en undergruppe av alle n røttene eller generere dem alle sammen. I det siste tilfellet kalles roten for primitiv. Den har den egenskapen at hvis roten x = zk er primitiv, så er den ikke en løsning av xm - 1 = 0 for noe positivt heltall m < n. For eksempel når n = 3, så er begge røttene 1/2(-1 ± i√3) primitive. Derimot for n = 4 er bare z = ± i primitive da (-1)2 = 1, mens (± i)2 = - 1. Når n er et primtall, så er generelt antall primitive røtter lik med n - 1.
Av formen for den generelle roten zk til sirkeldelingslinjen av grad n ser man at antall primitive røtter er gitt ved de verdier av k < n som er relativt primisk til n. Denne tallteoretiske egenskapen til n er uttrykt ved Eulers totientfunksjon φ(n). Da alle postive tall mindre enn et primtall p er relativt primiske til dette, vil φ(p) = p - 1. Denne aritmetiske funksjonen spiller en sentral rolle i den algebraiske bestemmelsen av hvilke regulære mangekanter som kan geometrisk konstrueres.
Se også[rediger | rediger kilde]
Litteratur[rediger | rediger kilde]
- A. Søgaard og R. Tambs Lyche, Matematikk for den høgre skolen, Gyldendal Norsk Forlag, Oslo (1955).
- J. Reed og J. Aarnes, Matematikk i vår tid, Universitetsforlaget, Oslo (1967).
- R. Courant and H. Robbins, What is Mathematics? An Elementary Approach to Ideas and Methods, Oxford University Press, Oxford (1996). ISBN 0-195-10519-2.
Eksterne lenker[rediger | rediger kilde]
- Devin Kuh, Constructible Regular n-gons Arkivert 24. april 2019 hos Wayback Machine., Senior Project, Whitman College (2013).










