Konstruksjon (geometri)

Konstruksjon i euklidsk geometri består i å konstruere nye punkt, linjestykker og sirkler med gitte egenskaper, kun ved bruk av passer og linjal. De to hjelpemidlene skal benyttes etter bestemte regler og kalles da euklidske hjelpemidler.
Grunnlaget for geometriske konstruksjoner ble lagt av matematikere i antikkens Hellas, og ikke minst har Euklids Elementer hatt en svært stor betydning. Helt fra oldtiden og fram til moderne tid har euklidsk geometri vært omfattende studert og videreutviklet. Mange kompliserte geometriske konstruksjoner og bevis kan bygges opp ved hjelp av et endelig antall standard konstruksjoner. Lengder som lar seg konstruere med euklidske hjelpemidler kalles konstruerbare tall eller euklidske tall og er en ekte delmengde av de reelle tallene.
Flere problemstillinger er ikke løsbare med euklidske hjelpemidler, og dette inkluderer de tre klassiske problemstillingene sirkelens kvadratur, kubens fordobling og vinkelens tredeling. Konstruksjonene kan imidlertid gjennomføres dersom en tillater andre typer hjelpemidler. Ved hjelp av analytisk geometri kan en føre bevis for hvilke typer problemer som lar seg løse med euklidske hjelpemidler.
Regler for lovlig bruk av passer og linjal[rediger | rediger kilde]
De to hjelpemidlene linjal og passer kan kun benyttes i konstruksjonen etter bestemte regler.[1] Linjalen skal være uten målestreker. Som utgangspunkt kan en bruke et endelig antall gitte punkt. Nye punkt kan konstrueres som skjæringspunkt mellom to linjer, mellom to sirkler og mellom en linje og en sirkel. To typer konstruksjon regnes som lovlige:
- Linjalen kan brukes til å trekke en linje gjennom to gitte punkt. Linjen kan forlenges uendelig i begge retninger.
- Passeren kan brukes til å lage en perfekt sirkel med et gitt punkt som sentrum, slik at sirkelbuen går gjennom et annet gitt punkt.
Reglene tillater altså ikke at passeren brukes til å flytte en gitt avstand. En kan tenke seg at den ideelle passeren kollapser straks det ene benet løftes fra papiret. En passer som oppfyller disse ideelle kravene kalles en euklidsk passer. En slik passer og en linjal uten målestreker kalles sammen euklidske hjelpemidler.
Når det likevel er lov å tegne to sirkler med samme radius, men med to ulike sentrum, så er dette fordi en slik konstruksjon er mulig ved å kombinere flere steg av de to lovlige operasjonene. Dette er vist i det følgende avsnittet To sirkler med lik radius. Bruk av en moderne passer er dermed likeverdig med en ideell passer.
Konstruksjon etter disse reglene er i samsvar med Euklids store verk Elementer.[2] Reglene tillater konstruksjoner som stemmer overens med de tre første av de fem postulatene som Euklid brukte som grunnlag for geometrien. Detaljer om hvordan disse reglene kom til å bli etablert er ikke kjent, men de ble praktisert før Euklid virket. Tradisjonen har knyttet opphavet til Platon, men det er tegn på at reglene var i bruk også før Platon.[3][4] Platon mente at linjer og sirkler var mer ideelle objekter en andre typer kurver.
Vanlige konstruksjoner[rediger | rediger kilde]
Ved hjelp av reglene for lovlig bruk av passer og linjal kan en gjennomføre en rekke typer grunnleggende konstruksjoner.[1] De følgende avsnittene viser noen slike, der reglene er brukt i streng form. Figurer er vist samlet på slutten av avsnittet.
Vanligvis vil en benytte seg av muligheten til å kunne kopiere en sirkel med en gitt radius. En vil også ikke tegne hele sirkler, men bare deler nødvendige for konstruksjonen. Kompliserte geometriske bevis kan gjennomføres ved å kombinere grunnleggende konstruksjoner i et endelig antall steg.
Halvering av en vinkel[rediger | rediger kilde]
Gitt tre punkt som danner en vilkårlig vinkel med toppunkt T og der ett av de andre punktene er A. Med en passer, slå en sirkel med sentrum i T gjennom punktet A. Sirkelen skjærer det andre vinkelbeinet i punktet B. Lag deretter to sirkler, med sentrum i henholdsvis A og B, som begge går gjennom toppunktet T. De to siste sirklene skjærer hverandre i et punkt C. Linjen gjennom T og C vil halvere vinkelen.
Mer vanlig utføres konstruksjonen ved å bruke to identiske sirkler med vilkårlig radius, med sentrum i henholdsvis A og B.
En vinkel har en og kun en halveringslinje. Denne linjen er det geometriske sted for punkt som ligger like langt fra de to vinkelbeina. Halveringslinjesetningen omtaler forhold mellom lengder i en trekant, når en av trekantens vinkler halveres. Sentrum i innsirkelen i en trekant ligger på det felles skjæringspunktet mellom de tre halveringslinjene til vinklene i trekanten.
En normal til en linje i et gitt punkt[rediger | rediger kilde]
Gitt en rett linje gjennom to punkt A og B. En normal til linjen gjennom B kan konstrueres ved først å slå en sirkel med sentrum i B gjennom A. Sirkelen skjærer linjen i A, men også i et annet punkt C. En ny sirkel tegnes med sentrum i A og gjennom C. Tilsvarende tegnes en tredje sirkel med sentrum i C gjennom A. De to siste sirklene skjærer hverandre i to punkt P og Q. En linje gjennom disse to punktene er en normal til linjen gjennom B.
Også i dette tilfellet er det mer vanlig å utføre konstruksjonen ved å bruke to identiske sirkler med vilkårlig radius, med sentrum i henholdsvis A og C. Normalen deler linjestykket AC i to like deler.
En normal fra et punkt ned på en linje[rediger | rediger kilde]
Gitt en rett linje gjennom to punkt, der ett av disse er A. Gitt et annet punkt P som ikke ligger på linjen. Slå en sirkel med sentrum i P gjennom A. Sirkelen skjærer linjen i A, men også i et annet punkt B. Deretter slå en ny sirkel med sentrum i A gjennom 'P og en tredje sirkel med sentrum i B gjennom P. De to siste sirklene skjærer hverandre i P, men også i punktet Q på motsatt side av linjen. En ny linje gjennom P og Q er normal til den opprinnelige linjen.
Dersom de to punktene A og B er sammenfallende, så vil linjen gjennom P og A være den søkte normalen.
Denne konstruksjonen kan for eksempel brukes til å konstruere normalen fra et trekanthjørne ned på den motstående siden. Den kan også brukes til å speile et punkt om en linje.
En midtnormal[rediger | rediger kilde]
Gitt to punkt A og B på en rett linje. For å konstruere en midtnormal til linjestykket AB, lag først en sirkel om A gjennom B. Tegn deretter en sirkel om B gjennom A. En rett linje gjennom de to skjæringspunktene for de to sirklene vil være en midtnormal. Midtnormalen deler AB i to like deler.
En parallell linje gjennom et gitt punkt[rediger | rediger kilde]
En parallell til en linje, gjennom et gitt punkt, kan konstrueres ved å kombinere de to metodene for konstruksjon av normalen til en linje. Gitt en rett linje og et punkt P som ikke ligger på linjen. Konstruer først en normal til linjen fra punktet P. Deretter konstrueres en ny normal til normalen gjennom P. Normalen til normalen er parallell med den opprinnelige linjen.
To sirkler med lik radius[rediger | rediger kilde]
De euklidske reglene tillater strengt tatt ikke at en kopierer lengder, og fra dette kan en ikke uten videre slå to vilkårlige sirkler med samme radius. Når en slik operasjon likevel er akseptabel, så er dette fordi en kan gjennomføre operasjonen ved hjelp av flere lovlige steg: Gitt en sirkel om punktet A gjennom punktet B. Anta at en ønsker å lage en sirkel om et vilkårlig tredje punkt P, med samme radius som i den gitte sirkelen. En kan da konstruere en parallell linje gjennom A til linjestykket gjennom BP. Deretter en parallell linje gjennom P til linjestykket AB. De to konstruerte parallellene vil skjære hverandre i et punkt Q. En kan nå slå en sirkel om P gjennom Q, og denne sirkelen vil ha samme radius som den opprinnelige.
En sirkel gjennom tre punkt[rediger | rediger kilde]
Gitt tre punkt A, B og C som ikke ligger på linje. En sirkel som skjærer alle tre punkt kan konstrueres slik: Trekk først to linjer, AB og AC. Konstruer deretter midtnormalen til AB og så midtnormalen til AC. De to midtnormalene skjærer hverandre i et punkt S, som vil være sentrum i den søkte sirkelen. Slå nå en sirkel om S gjennom A. Denne vil også gå gjennom B og C.
En sirkel konstruert på denne måten vil være en omskrevet sirkel til trekanten ABC.
Konstruksjon av gitte lengder[rediger | rediger kilde]
Utdypende artikkel: Konstruerbare tall
Ut fra et gitt linjestykke, definert som lengde 1, er det mulig å konstruere linjestykker med lengder svarende til både naturlige tall, rasjonale tall og irrasjonale tall. Lengder som lar seg konstruere i med et endelig antall steg med euklidske hjelpemidler, kalles for konstruerbare tall eller euklidske tall.[5][6] Mange irrasjonale tall er ikke konstruerbare. Et konstruerbart tall er alltid et reelt algebraisk tall, mens et transcendentalt tall aldri kan være konstruerbart. De konstruerbare tallene er derfor en ekte delmengde av de reelle tallene.
Nye linjestykker kan selvsagt lett konstrueres ved repetert addisjon og subtraksjon av to gitte linjestykker. Et vilkårlig linjestykke også kan enkelt deles i like deler, som vist i den venstre av figurene under for 3: Gitt to punkt A og B på en rett linje. Konstruer en normal i A og deretter en parallell til den opprinnelige linjen, gjennom et vilkårlig punkt C. På parallellen, sett av nye punkt i avstanden AB: D, E og F. (Dette er en lovlig konstruksjon, gjennomførbart i flere steg). Trekk så en linje gjennom F og B. Denne skjærer normalen i A i et punkt T. Trekk så linjer gjennom T og punktene D og F. Alle linjene gjennom T deler nå linjestykket AB i 3. Linjestykker definert ved forholdstall kan også konstrueres ved hjelp av transversalteoremet.
Dersom og er konstruerbare lengder, så vil også både og være konstruerbar. En størrelse uttrykt som et produkt mellom to gitte lengder lar seg imidlertid ikke konstruere som en lengde, uten at en velger en enhet. For å se at dette er nødvendig, anta at lengden er kortere enn . Dersom enheten er valgt slik at , så vil produktet ha en lengde kortere enn . Velges derimot enheten slik at , så er produktet lenger enn . I gresk matematikk var et produkt alltid et areal, ikke en lengde.[7] Et begrep som «enhetslengde» var ikke brukt i klassisk euklidsk geometri. Heller ikke størrelsen kan konstrueres uten at en enhetslengde er kjent.
Til gjengjeld er det lett å konstruere et linjestykke med lengde . Greske geometer brukte ofte forholdstall, og er mellomproporsjonalen, gitt ved forholdet[8]
Anta at tre punkt A, B og C er definert på en linje, slik at AB = og BC = . Konstruer en sirkel som har AB som diameter. Konstruer normalen fra B. Der normalen skjærer sirkelen, definer punktet D. Den søkte mellomproporsjonalen er linjestykket BD. Konstruksjonen er vist i den høyre figuren under.
En rettvinklet trekant kan selvsagt brukes til å konstruere mange lengder svarende til tall med kvadratrøtter, noe som følger direkte av Pythagoras’ læresetning. For eksempel gir en rettvinklet trekant med kateter med lengder henholdsvis 1 og 2 hypotenusen som et linjestykke med lengde . Konstruksjon av det gyldne snitt kan også gi et linjestykke med lengde
|
Konstruksjon av gitte vinkler[rediger | rediger kilde]
Vinkelsummen i en trekant er lik summen av to rette vinkler, det vil si radianer eller 180°, et resultat som var kjent allerede blant de greske pytagoreerne. I en likesidet trekant er alle vinklene like store, så dette må igjen være like en tredel av to rette vinkler. En linje som skjærer en annen linje i en vinkel på 60° lar seg dermed lett konstruere. Gitt en rett linje gjennom to punkt A og B. Slå en sirkel om A gjennom B. Deretter slå en sirkel om B med samme radius. En linje gjennom A og skjæringspunktet mellom de to sirklene vil være den søkte linjen.
En rekke andre tallfestede vinkler lar seg konstruere ved hjelp av normaler, 60°-vinkler og vinkelhalveringer.
En gitt vinkel er konstruerbar hvis og bare hvis og er konstruerbare lengder. I en rettvinklet trekant med hypotenus lik 1, er og lengdene av de to katetene, når er en vinkel i trekanten.
Regulære mangekanter[rediger | rediger kilde]

Utdypende artikkel: Regulær mangekant
Regulære mangekanter har vært kjent i flere tusen år.[9] Dette er figurer der alle sidene er like lange og all hjørnevinklene er like store. De enkleste eksemplene er en likesidet trekant og et kvadrat. Hjørnene i en regulær mangekant vil alltid ligge på en omsirkel med sentrum i tyngdepunktet i mangekanten. Sentralvinkelen i en -kant er lik eller 360°, og konstruksjon av en mangekant svarer til konstruksjon av denne vinkelen.
Allerede i Euklids Elementer ble det vist at også en regulær pentagon (femkant) lar seg konstruere geometrisk. Her er sentralvinkelen 360°/5 = 72°, som tilsvarer 2π/5 radianer. Cosinus til sentralvinkelen er et konstruerbart tall:
Fra en kjent mangekant kan en konstruere nye mangekanter med flere hjørner, ved å halvere vinklene mellom sideflatene og bruke skjæringspunktene mellom omsirkelen og halveringslinjene som nye hjørnepunkt. Fra en trekant kan en slik konstruere en regulær heksagon (sekskant), der sentralvinklene er 60°, en vinkel som er lett konstruerbar. Fra et kvadrat kan en tilsvarende lage en oktogon, en 8-kant. En 10-kant kan konstrueres fra en 5-kant, og så videre. I praksis er det lettest å konstruere en 10-kant først, deretter en 5-kant.[9]
Med euklidske hjelpemidler er det ikke mulig å konstruere en regulær 7-kant og en regulær 9-kant. Lenge var det en utbredt oppfatning at det ikke er mulig å konstruere andre regulære mangekanter enn 3- og 5-kanten med et odde antall kanter. Carl Friedrich Gauss beviste imidlertid at en regulær -kant er konstruerbar med euklidske hjelpemidler dersom[10]
- ,
der og alle er primtall på formen
- .
Primtall som kan skrives på denne formen kalles Fermat-primtall. Verdiene og gir henholdsvis og . Neste verdi gir at mangekanten med er konstruerbar.
Gauss viste også at[trenger referanse]
- ,
et tall som kan konstrueres.
Gauss var kun 18 år da han i 1796 som student ved Universitetet i Göttingen viste at heptadekagonet (17-kanten) kan konstrueres, og resultatet ble publisert i 1801 som del av den generelle teorien i verket Disquisitiones arithmeticae.[11] Han hevdet der, uten bevis, at uttrykket for også er nødvendig for at det regulære polygonet skal være konstruerbart, men dette ble først vist i 1837 av Pierre Wantzel.[trenger referanse] Selve konstruksjonen av heptadekagonet ble heller ikke gjennomført av Gauss, dette ble først gjort av Johannes Erchinger, noen år etter arbeidet til Gauss.[10]
Bare fem Fermat-primtall er kjent: 3, 5, 17, 257 og 65537. Konstruksjoner er gjennomført både for den regulære 257-kanten og den regulære 65537-kanten.[12][13]
|
Geometrisk algebra[rediger | rediger kilde]

Som omtalt i avsnittet Konstruksjon av gitte lengder, ble produkt av to lengder i euklidsk matematikk behandlet som et areal. Problemstillinger som involverte areal var grunnleggende for gresk geometri. Problemene var ofte formulert som et ønske om å finne siden i et kvadrat med samme areal som en annen figur eller som en sum/differanse av flere andre figurer. I generell form er slike problemstillinger ekvivalent til å løse en andregradsligning. Studiet av slike problemstillinger er omtalt som geometrisk algebra.[14]
En problemstilling der løsningen antagelig har vært kjent allerede av pytagoreerne, svarer til å finne en enkelt løsning av ligningen[14]
Alle størrelser i ligningen kan uttrykkes som areal, slik at problemstillingen kan formuleres ved hjelp av ord, uten å kreve ligninger. Konstruksjon av en løsning er vist i figuren under: La linjestykket AB ha lengde . Konstruer midtnormalen til dette linjestykket, og la C være halveringspunktet på AB. La D være et punkt på midtnormalen, i avstand fra C. Tegn en sirkel med sentrum i D og med radius . For at dette skal være mulig, så må . La E være et skjæringspunkt mellom sirkelen og linjestykket AB. Den ukjente svarer til lengden av linjestykket EB. Bevis for at dette er rett brukte en geometrisk form for konjugatsetningen, som var kjent for pytagoreerne:
Fra Pythagoras' læresetning er . I tillegg er og . Ved å kombinere disse får man en geometrisk form for ligningen:
Også arabiske matematikere som tok opp arven etter grekerne, var opptatt av problemstillinger svarende til andregradsligninger, løst ved geometriske konstruksjoner. Dette gjelder ikke minst for al-Khwârizmî, som er blitt kalt for «algebraens far».[15]
Umulige konstruksjoner[rediger | rediger kilde]
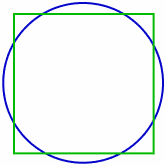
Flere problemstillinger skapte betydelige utfordringer for klassisk geometri. De tre mest kjente slike problemene er[16]
- Sirkelens kvadratur: Gitt en sirkel, konstruer et kvadrat med samme areal.
- Kubens fordobling: Gitt en kube, konstruer en annen kube med det dobbelte volumet.
- Vinkelens tredeling: Gitt en vilkårlig vinkel, konstruer en vinkel som er en tredjedel av den opprinnelige vinkelen.
Når disse klassiske problemene i dag ofte omtales som «umulige», må dette forstås som «umulige ved hjelp av euklidske hjelpemidler». Allerede i gresk geometri fant en mulige konstruksjonsmåter ved å tillate andre typer hjelpemidler og andre regler enn de euklidske.[1]
En full forståelse for hva som er mulig og ikke mulig innenfor de euklidske reglene, kom først nesten to tusen år etter Euklid, med etableringen av analytisk geometri. Arealet av sirkel er gitt ved , og løsning av sirkelens kvadratur krever konstruksjon av tallet . Ferdinand von Lindemann viste i 1882 at tallet er transcendentalt og dermed ikke konstruerbart.[17] Pierre Wantzel viste i 1837 at både kubens fordobling og vinkelens tredeling krever geometrisk løsning av en tredjegradsligning og ikke er løsbare med euklidske hjelpemidler.[18]
Analytisk geometri[rediger | rediger kilde]
Analytisk geometri kan brukes til å utforske grensene for hva som er mulig og ikke mulig av euklidske konstruksjoner. I analytisk geometri kombineres geometri og algebra, og metoder fra matematisk analyse brukes til å analyse koordinater til geometriske objekter, inkludert de tre grunnleggende objektene punkt, linje og sirkeli euklidsk geometri. Et punkt i planet kan representeres i et kartesisk koordinatsystem ved to reelle koordinater . En linje konstruert gjennom to punkt og har ligningen
- ,
forutsatt at nevneren ikke er null. En sirkel med sentrum i gjennom punktet har ligningen
der er sirkelradien. Nye punkt i euklidsk geometri blir konstruert som skjæringspunkt mellom to linjer, mellom to sirkler eller mellom en linje og en sirkel. Koordinatene til slike skjæringspunkt finner en da generelt som løsning av de to ligningene som beskriver de to objektene. Dette vil høyst være algebraiske ligninger (polynomligninger) av andre grad. Ligningene kan ha ingen, én eller to løsninger, svarende til ingen, ett eller to skjæringspunkt. Har ligningene uendelig mange løsninger, så er de to objektene sammenfallende.
Når en linje skjærer en sirkel, vil en enkelt løsning av ligningssettet svare til at linjen tangerer sirkelen. Det samme gjelder dersom ligningene for skjæringspunktene mellom to sirkler gir sammenfallende løsning - de to sirklene tangerer hverandre.
I analytisk geometri kan geometriske konstruksjoner uttrykkes som algebraiske ligninger. Om en konstruksjon er mulig eller ikke, blir da et spørsmål om ligningene har løsninger eller ikke. Disse sammenhengene ble først fullstendig forstått i begynnelsen av 1800-tallet, gjennom arbeidene til Niels Henrik Abel og Évariste Galois.[trenger referanse]
Konstruerbarhet[rediger | rediger kilde]
Siden de euklidske hjelpemidlene ikke tillater at en måler lengden på linjestykker, vil alle lengder og størrelser måtte avledes fra posisjonen til de først gitte punktene. Antallet gitte punkt skal være endelig, og det er dermed mulig å velge en lengdeenhet som gjør at alle koordinatene til de først gitte punktene er heltall. De første skjæringspunktene en bestemmer vil derfor være gitt som løsning av algebraiske ligninger av høyst grad to og med heltallskoeffisienter. Løsningene kan generelt uttrykkes som en kombinasjon av rasjonale tall og kvadratrøtter. Når man så går videre i konstruksjonen, vil man benytte disse skjæringspunktene som utgangspunkt for nye linjer og sirkler. Det vil igjen gi opphav til nye skjæringspunkt, og koordinatene til disse vil i alminnelighet være rasjonelle uttrykk og kvadratrøtter av de forrige skjæringspunktene. Dette betyr at koordinatene vil kunne inneholde kvadratrøtter av kvadratrøtter av de opprinnelige, gitte punktene. Slik vil det fortsette videre i konstruksjonen, inntil den er avsluttet etter et endelig antall steg.
Fra en euklidsk geometrisk konstruksjon kan det altså kun fremkomme størrelser som er en endelig kombinasjon av rasjonelle tall og kvadratrøtter, der kvadratrøttene igjen kan inneholder kvadratrøtter og så videre et endelig antall ganger. Kubikkroten kan ikke uttrykkes på denne måten og er derfor ikke et konstruerbart tall. Dette er også grunnen til at kubens fordobling ikke lar seg gjennomføre med euklidske hjelpemidler.
Andregradsligningen[rediger | rediger kilde]

Grunnlaget for analytisk geometri ble etablert av René Descartes og Pierre de Fermat.[19] Descartes ga i 1637 ut arbeidet La Géométrie, som et tillegg til verket Discours de la Méthode. I første del av dette tillegget drøfter han problemer som er løsbare ved hjelp av passer og linjal, og dette inkluderer løsning av flere andregradsligninger. Én slik ligning kan skrives på formen[20]
- .
Metoden forutsetter at er positiv og at .
I et kartesisk koordinatsystem tegner man først en sirkel med radius og med sentrum på -aksen i punktet . Denne sirkelen vil gå gjennom origo O og punktet . Dette er vist i figuren til høyre, med .
Deretter trekker man linjen , parallelt med -aksen. Når vil denne skjære sirkelen i to punkt, og -koordinatene til de to skjæringspunktene er røttene og i ligningen.
Forklaringen følger lett fra en analytisk beskrivelse. Sirkelen er beskrevet ved ligningen
Setter man her , får man
- .
Dette svarer til den opprinnelige ligningen, med de to røttene
- .
Skjæringspunktene ligger på samme side av origo, og fortegnet i røttene er alltid like.
Bruk av koeffisient-formen er nødvendig for at konstruksjonen generelt skal være euklidsk. Også matematikere i middelalderen, inkludert François Viète, hadde i studiet av ligninger krevd at størrelser skulle være sammenlignbare, og at en ikke kunne blande uttrykk for en lengde med et areal .[21] Descarets sprengte rammene for den klassiske geometrien, ved å betrakte også som en lengde.
Carlyle-sirkelen[rediger | rediger kilde]

Det skulle gå omtrent to hundre år fra Descartes La Geométrie før en generell, geometrisk konstruksjon av røttene til andregradsligningen ble funnet av Thomas Carlyle.[trenger referanse] Metoden tar utgangspunkt i ligningen
- .
Man angir i et kartesisk koordinatsystem de to punktene A = (0,1) og B = (s,p). Når en sirkel så blir konstruert med linjestykket AB som diameter, vil dens skjæringspunkt med -aksen være røttene og .
Denne Carlyle-sirkelen kan finnes både for positiv og negativ verdi av . For det siste tilfellet er konstruksjonen vist i figuren til høyre. Punktet B ligger da under -aksen, og skjæringspunktene med -aksen ligger på hver sin side av origo. Dette er i samsvar med at røttene i ligningen i dette tilfellet har forskjellige fortegn.
En analytisk forklaring av konstruksjonen er denne gangen noe mer omstendelig. Sirkelradien er lik halve diameteren AB, og det vil si
Sirkelens sentrum M ligger i midtpunktet av linjestykket AB, med koordinatene . Sirkelen er nå gitt ved ligningen
- .
Setter man her , følger så de korrekte uttrykkene for begge røttene. For positiv gir denne konstruksjonen selvsagt samme resultat som konstruksjonen til Descartes.
Ikke-euklidske hjelpemidler[rediger | rediger kilde]
Studiet av de klassiske «umulige» problemene fikk mange greske matematikere til å ta i bruk hjelpemidler som bryter med de euklidske reglene, både mekaniske hjelpemidler og andre geometriske objekter enn punkt, linje og sirkel. Eratosthenes, som levde omkring 200 år før Kristus, laget et mekanisk instrument for å kunne duplisere en kube.[22] For tredeling av en vinkel tok Nikomedes utgangspunkt i en kurve kalt en konkoide, som han konstruerte ved hjelp av et egenutviklet mekanisk instrument. En slik høyere-ordens kurve kan konstrueres med et uendelig antall euklidske steg, så konstruksjonen kan kalles asymptotisk euklidsk.[23] En kurve som kan brukes sammen med passer og linjal til å tredele en vinkel, kalles en trisektrise. En kurve som kan benyttes til sirkelens kvadratur kalles en kvadratrise. Arkhytas brukte tredimensjonale objekter for å duplisere en kube, ved å snitte en sylinder, en kjegle og en torus.[24]
Greske matematikere benyttet seg også av en konstruksjonstype kalt neusis-konstruksjon, der det ble brukt en linjal med måleenheter.
Den arabiske matematikeren Abu l-Wafa (940-998) gjorde forsøk på å se hvor mye han klarte å konstruere med en «rusten passer», det vil si en passer som har en fast passeråpning og dermed bare kan tegne sirkler med en gitt radius. Med et slikt hjelpemiddel er det faktisk mulig å gjennomføre alle konstruksjoner som kan utføres euklidsk.[25]
Alle punkt som kan konstrueres euklidsk, kan overraskende nok konstrueres ved hjelp av kun en passer, et resultat som ble vist av italieneren Lorenzo Mascheroni (1750-1800). Ved å ta utgangspunkt i en parabel med kjent brennpunkt og direktrise, kan også alle euklidske konstruksjoner gjennomføres kun ved hjelp av en linjal.[25]
Referanser[rediger | rediger kilde]
- ^ a b c A. Holme: Geometry. Our cultural heritage. s.48-50
- ^ A. Holme: Matematikkens historie (Bind 1) s.259ff
- ^ Carl B.Boyer (2004). History of analytical geometry. New York: Dover Publications. s. 13-14. ISBN 0-486-43832-5.
- ^ T. Heath A history of Greek mathematics (Vol. I) s.288
- ^ A. Holme: Geometry. Our cultural heritage. s.331ff
- ^ G.H. Hardy, E.W. Wright: An introduction to the theory of numbers s.204
- ^ A. Holme: Matematikkens historie (Bind 1) s.242f
- ^ A. Holme: Matematikkens historie (Bind 1) s.212
- ^ a b A. Holme: Geometry. Our cultural heritage. s.340ff
- ^ a b G.H. Hardy, E.W. Wright: An introduction to the theory of numbers s.71ff
- ^ : C.B.Boyer; A history of mathematics s.544ff
- ^ «257-gon». Wolfram MathWorld. Besøkt 5. mars 2021.
- ^ «65537-gon». Wolfram MathWorld. Besøkt 5. mars 2021.
- ^ a b T. Heath A history of Greek mathematics (Vol. I) s.150ff
- ^ : C.B.Boyer; A history of mathematics s.252
- ^ A. Holme: Geometry. Our cultural heritage. s.50-56
- ^ G.H. Hardy, E.W. Wright: An introduction to the theory of numbers s.228
- ^ Florian Cajori (1918). «Pierre Laurent Wantzel». Bull. Amer. Math. Soc. 24: 339–347.
- ^ Carl B. Boyer (2013). «Analytic geometry: The discovery of Fermat and Descartes». I Frank J. Swetz. The European Mathematical Awakening. Mineola, New York: Dover Publications. s. 134ff. ISBN 0-486-49805-0.
- ^ : C.B.Boyer; A history of mathematics s.370ff
- ^ A. Holme: Matematikkens historie (Bind 2) s.259ff
- ^ A. Holme: Geometry. Our cultural heritage. s.93
- ^ A. Holme: Geometry. Our cultural heritage. s.95-96
- ^ A. Holme: Geometry. Our cultural heritage. s.59ff
- ^ a b A. Holme: Geometry. Our cultural heritage. s.330
Litteratur[rediger | rediger kilde]
- J. Reed og J. Aarnes, Matematikk i vår tid, Universitetsforlaget, Oslo (1967).
- Audun Holme (2002). Geometry. Our cultural heritage. Berlin: Springer-Verlag. ISBN 3-540-41949-7.
- Audun Holme (2008). Matematikkens historie. 1 og 2. Bergen: Fagbokforlaget. ISBN 978-82-450-0697-1.
- Carl B.Boyer (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3.
- Thomas Heath (1981). A history of Greek mathematics. I. New York: Dover Publications. ISBN 0-486-24073-8.
- G.H. Hardy, E.W. Wright (2008). An introduction to the theory of numbers. Oxford: Oxford University Press. ISBN 978-0-19-921985-8.



























































![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)



















