Elektrisk effekt

De tre kløfters demning er verdens største kraftverk, det er dermed verdens største elektriske energikilde. Effekt er et mål på hastighet for energi­omsetning, og dette vannkraftverket er også verdens største elektriske effektkilde.

Foto: Allen Watkin

Analogt bærbart måle­instrument for både aktiv- og reaktiv effekt.

Foto: Hungarikusz Firkász

Elektrisk effekt er mottatt eller avgitt elektrisk energi per tidsenhet i en elektrisk krets. På samme måte som mekanisk effekt blir elektrisk effekt målt i watt (W). Én watt er lik 1 joule per sekund. Den enkle sammenheng mellom effekt, strøm og spenning i en elektrisk krets er at effekten er produktet av strøm og spenning.

Sammenhengen mellom strøm, spenning og effekt er noe mer komplisert når det gjelder elektriske kraftsystemer med vekselstrøm. I vekselstrømsystemer er strøm og spenning beskrevet av sinusfunksjoner, dermed vil også produktet av strøm og spenning bli en sinusfunksjon. Siden dette er verdier som varierer over tid, angir man ofte effekt uttrykt ved middelverdien av denne. Konseptet innebærer at effekten som en vekselstrøm og -spenning representerer gjøres sammenlignbar med den effekten som en tilsvarende stor likestrøm og -spenning ville gitt. Ytterligere mer komplisert blir sammenhengen om vekselstrømssystemet er et trefasesystem. Da må det tas hensyn til at både strømmer og spenninger har en innbyrdes faseforskyvning. Rent fysisk er faseforskyvning en innbyrdes tidsforsinkelse av de periodiske signalene. Utledning av formlene som gjelder involverer en del avanserte matematiske konsepter, men formlene som til slutt fremkommer er dog enkle.

En spesiell sammenheng som finnes i systemer for vekselstrøm er at det oppstår en type elektrisk effekt som bare sirkulerer i kraftsystemet, dermed kan den ikke omformes til andre energiformer som varme, lys, lyd, mekanisk arbeid, eller tjene andre nyttige hensikter. Denne energien har sammenheng med elektriske- og magnetiske felter som alltid er tilstede i et elektrisk system. En kaller denne effekten for reaktiv effekt, mens den anvendbare effekten kalles aktiv effekt. Et måltall på andelen av reaktiv effekt relativt til aktiv effekt i et kraftsystem er effektfaktoren, som egentlig angir faseforskyvningen mellom gitt strøm og spenning. Reaktiv effekt fører til unødvendig energitap i elektriske kraftlinjer. Dermed er dette en type effekt som blir forsøkt begrenset på forskjellige vis.

Notasjon og måleenheter

Både elektrisk effekt, og effekt i andre sammenhenger måles i watt med forkortelsen W, etter den skotske fysikeren James Watt. En watt er lik 1 joule per sekund: 1 W = 1 J/s. For vekselstrøm har en også måleenhetene voltamper (VA) for tilsynelatende effekt og voltamper-reaktiv (VAr) for reaktiv effekt. Voltamper brukes for å oppgi nominell ytelse for elektriske maskiner som generatorer, motorer, transformatorer og lignende. Voltamperereaktiv brukes for å oppgi effekten til blant annet spoler, reaktorer og kondensatorer. I de fleste sammenhenger er det middelverdien av effekten som er av interesse, men for elektriske kretser for vekselstrøm vil den såkalte momentanverdien (verdien på et gitt tidspunkt) også være en størrelse som i noen tilfeller undersøkes.

Måleenheter som for eksempel (kWh) (uttales «kilowattime») eller (MWh) (uttales «megawattime») er vanlige enheter for elektrisk energi, spesielt ved kjøp og salg. Således er 1 kWh den energimengden som omsettes om effekten 1 kW konstant produseres eller forbrukes i én time.

Generell definisjon på effekt

Grunndefinisjonen av effekt i fysikken er at det er arbeidet per tidsenhet som blir mottatt eller opptatt. Med andre ord uttrykker det hvor raskt arbeid blir utført. Dette er blant annet et sentralt begrep i klassisk mekanikk, der en definerer middelverdien av effekt P_mid over en tidsperiode med varighet Δt slik:

$P_{mid}={\frac {\Delta W}{\Delta t}}\,$

der ΔW er arbeidet som utføres i den samme tidsperioden. Momentant utviklet effekt er grenseverdien av uttrykket over når tidsintervallet Δt går mot null. Dette er det samme som den deriverte av arbeidet:

$p=\lim _{\Delta t\rightarrow 0}P_{mid}=\lim _{\Delta t\rightarrow 0}{\frac {\Delta W}{\Delta t}}={\frac {\mathrm {d} w}{\mathrm {d} t}}\,$

Her uttrykker små bokstaver for effekt p og arbeid w at en har med tidsvariable størrelser å gjøre.

Om arbeidet som utvikles per tidsenhet er konstant er det ikke nødvendig å forholde seg til et derivat, og uttrykket forenkles slik:

$P={\frac {W}{t}}$

Når effekten behandles som en effektivverdi benyttes stor bokstav P. Skillet mellom små og store bokstaver følger av konvensjoner brukt innen elektroteknikk.

Effekt i likestrømskretser

Elektrisk effekt

Elektrisk energi har å gjøre med en elektrisk strøm av ladningsbærere. En strøm drives frem av en spenning. Spenning er definert som differansen av elektrisk potensial mellom to punkter i et elektrisk felt per ladningsenhet. Dette uttrykkes matematisk som

$u={\frac {dw}{dq}},$

der w er energi målt i joule, som tidligere definert, og q er ladning målt i coulomb. Definisjonen av strøm er at dette er en parameter for ladninger som passerer et tverrsnitt av en leder per tidsenhet. Matematisk skrives dette

$i={\frac {dq}{dt}},$

med samme betydning for q og t som definert tidligere. Med disse to definisjonene kan en utlede en meget enkel formel for elektrisk effekt:

$p={\frac {\mathrm {d} w}{\mathrm {d} t}}=\left({\frac {\mathrm {d} w}{\mathrm {d} q}}\right)\left({\frac {\mathrm {d} q}{\mathrm {d} t}}\right)=ui\,$

der:

p = elektrisk effekt i watt
u = spenning i volt og
i = strømmen i amper.

Strøm og spenning er parametere som benyttes for analyse av elektriske kretser eller kraftsystemer. Elektrisk effekt gir også informasjon om effekten eller energien generert av en elektrisk krets. Overføring av effekt og energi er ofte selve nytten av den elektriske kretsen, apparatet eller systemet. En annen grunn til å se på elektrisk effekt er at praktiske apparater har en begrensning på hvor mye effekt de kan håndtere. Ved konstruksjon av elektriske apparater og systemer er det derfor nødvendig å ta hensyn til effekt, ikke bare strøm og spenning.

Retningen på elektrisk effekt

Animasjon som fore­stiller en elektrisk last, for eksempel en lampe

Animasjon som fore­stiller en elektrisk kilde, for eksempel ett batteri.

Av ligningen i avsnittet over ser en at effekt er produktet av strøm gjennom elementet og spenningen over det. Effekt utviklet eller absorbert i et kretselement skjer mellom dets to terminaler, og denne effekten kan ha positivt eller negativt fortegn.

I den øverste animasjonen til høyre går det en strøm av ladninger gjennom et kretselement der den øverste terminalen har positivt potensial (merket «+») og den nederste negativt (merket «-»). Strømmen går inn ved plussterminalen, dermed sier en at en ladning q som går gjennom elementet får redusert sin potensielle energi. Når dette skjer får heller ikke ladningen tilført kinetisk energi fordi strømmen av ladninger inn og ut av elementet må være like stor. Det skjer altså en overføring av elektrisk energi inn til elementet som omdannes til en annen energiform og forlater den elektriske kretsen. Animasjonene illustrere dette som piler ut fra kretselementet.

Spenningsfallet over kretselementet i begge tegningene defineres til å være et positivt tall. Energitapet er gitt av qU, som representerer mengden elektrisk energi som går inn til elementet og omskapes til for eksempel varme, lys, eller mekanisk arbeid. Animasjonene nedenfor til høyre viser et motsatt tilfelle der strømmen går ut ved den positive terminalen. Da omformes energi utenfra, som går ut av elementet som elektrisk energi. Dermed oppfører den seg som en spenningskilde. Produktet av ladning og spenning må dermed være negativt, altså -qU. Det er her sett på én ladning, og hvordan den tilføres eller avgir energi. Med definisjonen om at strøm er ladninger per tidsenhet kan en like god skrive i istedenfor q, altså som henholdsvis iU og -iU.

Den definisjonen som er brukt her for energiretning kalles for motorisk referanseretning. Med denne definisjonen forårsaker strøm (ladninger) som går inn ved den positive terminalen at det utføres arbeid i komponenten, altså at uttrykket iU er positivt. Omvendt vil strøm som flyte fra negativ til positiv terminal bety at arbeid tilføres komponenten. Her får en at produktet av strøm og spenning er negativt.

Eksempel på beregning av effekt for en likestrømskrets

Mellom Celilo i Oregon og Sylmar i California går det en overføringslinje for likestrøm (HVDC). Denne har en nominell spenning på 500 kV og kan har en største strømstyrke på 6,2 kA. Hvor mye effekt kan overføres?

Ved bruk av formelen for effekt utledet over setter en inn tallene og får:

$P=UI=500\cdot 10^{3}\ V\cdot 6,2\cdot 10^{3}\ A=3,1\cdot 10^{9}\ W=3100\ MW$

Legg merke til at det her er benytte store bokstaver for effekt, spenning og strøm fordi parametrene i dette tilfellet er tidsuavhengige.

Effekt og resistans

Resistorer av ulike størrelser til bruk i elektroniske apparater. Leg merke til at noen har lesbar nøyak­tighet i prosent, mens i alle fall enhet nummer to fra høyre har påtrykket nominell effekt.

Sirkel­diagram som viser Ohms lov kombinert med effekt­formelen på mange forskjellige måter.

I elektriske kretser er elektrisk motstand en viktig parameter. Om motstand opptrer som et eget konsentrert kretselement snakker en om en resistor. Motstand er en egenskap med alle elektriske ledere unntatt superledere, og har den egenskapen at elektrisk energi omformes til varme i elektriske apparater eller kraftoverføringer. Dette betyr tap av energi, og er derfor ofte uønsket. Imidlertid kan denne egenskapen være høyst ønsket i for eksempel en varmeovn eller en brødrister.

Elektroner som blir akselerert i det elektriske feltet som spenningskilden forårsaker gjennom resistoren, mister energi ved kollisjoner med atomene i lederen. Dette fører til atomære vibrasjoner som igjen fører til at termisk energi utvikles i resistoren. Temperaturen i resistoren vil øke eller den avgir varmeenergi til omgivelsene, eller begge deler skjer samtidig. For enhver resistor er det vanlig å oppgi en nominell effekt, det vi si høyeste effekt den kan yte uten å bli overopphetet og ta skade. Ved valg av resistorer ved konstruksjon av elektriske apparater er valg av ytelse like så viktig som å velge riktig motstandsverdi. Selv en elektrisk varmeovn eller et annet apparat konstruert for å avgi varme kan ta skade om effektavgivelsen blir for stor. Også ledere som er konstruert for minst mulig motstand og varmeutvikling kan få ugunstig høy temperatur om belastningen blir for stor. Spesielt elektriske kabler for høyspenning med tykk elektrisk isolasjon kan ta skade om en ikke tar hensyn til varmeavgivelse til omgivelsene. Utsettes aluminiumslinene i en kraftledning for sterk sollys og høy lufttemperatur kan høyeste tillatte strøm bli betydelig redusert, sammenlignet med om de står i skygge, vind og lav temperatur.

Forholdet mellom strøm i, spenning u og motstand R i metalliske ledere er beskrevet av Ohms lov, gitt ved:

$u=iR\,$

der det forutsettes at R er uavhengig av tid. Om en setter inn for Ohms lov i uttrykket for effekt kan dette kombineres på forskjellige måter:

$p=ui=i^{2}R={u^{2} \over R}$

Dette gir altså tre måter å finne effekten som utvikles i en krets med resistans. Figuren til høyre viser enda flere måter dette forholdet kan kombineres på for å finne effekt, spenning, motstand og strøm om to av størrelsene allerede er kjent.

Effekt i sammenheng med vekselstrømskretser

Effekt i sammenheng med vekselstrømskretser er mer komplisert enn for likestrøm. Det er nødvendig å ha kjennskap til en del grunnlegende begreper og konsepter innenfor vekselstrømsteknikk for å kunne forstå hvordan effekt beskrives i slike elektriske kretser. Derfor inneholder dette kapittelet en del innledende beskrivelser.

Sinusformet vekselstrøm og spenning

Utdypende artikkel: Vekselstrøm

Fremstilling av en sinus­funksjon over en periode på 360°. Om frekvensen er 50 Hz er periode­tiden T lik 20 ms. Dermed svarer 0º til 0 ms, 90º til 5 ms, 180º til 10 ms, 270º til 15 ms og 360º til 20 ms. De stiplede linjene repre­senterer verdien av kurven når middel­verdi­beregningen kalt effektivverdi (rms) blir beregnet. Denne verdien er et irrasjonelt tall med tilnærmet verdi på 0,707 for en sinus­formet strøm eller spenning.

En vekselspenningskilde produserer en elektromotorisk spenning som har en verdi som variere med tiden og beskrives med en sinusfunksjon. Vekselspenningskilden kan være en generator. Tilknyttes spenningskilden en ytre krets vil det også gå en sinusformet strøm i kretsen. Dette forutsatt at kretsen består av såkalte lineære kretselementer. Lineære kretselementer følger Ohms lov, mens andre typer elementer som for eksempel dioder, transistorer, lysbuer ikke gjør det. For disse lineære elementene vil det oppstå et spenningsfall som også er sinusformet. En generell sinusformet vekselspenning og -strøm kan skrives:

$u={\hat {u}}\cos(\omega t+\theta _{u})$

$i={\hat {\imath }}\cos(\omega t+\theta _{i})$

der

$i$ = momentanverdien av strømmen i tidspunktet t (A)

$u$ = momentanverdien spenningen i tidspunktet t (V)

${\hat {\imath }}$ = amplitude for strømmen, i absoluttverdi lik strømmens maksimums- og minimumsverdi (A)

${\hat {u}}$ = amplitude for spenningen (V)

$\omega \,$ = vinkelfrekvens i radianer (rad) eller grader, per sekund (s^-1 eller °s^-1)

$t$ = tid (s)

$\theta _{u}$ = faseforskyvning, eller fasevinkel, for spenningen (rad eller grader)

$\theta _{i}$ = faseforskyvning for strømmen

Figuren til høyre viser et sinusformet signal, der verdiene langs x-aksen ikke er tiden, men grader.

Tiden for en periode, periodetiden, er gitt ved

$T={\frac {2\pi }{\omega }}$

Antall perioder per sekund, frekvensen, er

$f={\frac {\omega }{2\pi }}={\frac {1}{T}}$

Vinkelfrekvensen som er brukt i funksjonene over er gitt av følgende sammenheng:

$\omega =2\pi f$

Enheten for frekvens er Hz, for perioden s og for vinkelfrekvens (s⁻¹).

Effektivverdien av sinusformet strøm og spenning

Utdypende artikler: Effektivverdi og Gjennomsnitt

Et digitalt multi­meter måler typisk strøm og spenning som blir vist som en effektiv­verdi på en skjerm.

Foto: Becky Stern

Tidsvarierende spenninger og strømmer er upraktiske størrelser for kalkulasjoner og beregninger, og en generell måte å beskrive en størrelse som kan være både positiv og negativ er ved hjelp av effektivverdier eller rms-verdier. Bakgrunnen for denne «effektive» verdien er ønske om å sammenligne en vekselstrøms (eller spennings) energiavgivelse til en ohmsk motstand med en tilsvarende stor likestrøms (eller spennings) energiavgivelse på den samme motstanden.

Begrepet rms er vanlig i norsk ordbruk, og står for root-mean-square, kvadratisk gjennomsnitt. Metoden går ut på at størrelsen, her en kontinuerlig sinusfunksjon for strøm eller spenning først kvadreres, så finner en gjennomsnittet og deretter tas kvadratroten av dette.

Formelen for rms for en generell tidsvarierende spenning er:

$U_{\mathrm {rms} }={\sqrt {{\frac {1}{T}}\int _{0}^{T}{[u(t)]^{2}dt}}}.$

Ut fra dette kan en utlede sammenhengen mellom toppverdien og effektivverdien av en sinusformet spenning:

$U_{rms}={\frac {\hat {u}}{\sqrt {2}}}$

Dette kalles altså effektivverdien eller rms av en sinusformet vekselspenning. Formelen og utledningen for en vekselstrøm er tilsvarende gitt ved

$I_{rms}={\frac {\hat {\imath }}{\sqrt {2}}}$

Ofte skriver en bare U eller I når en mener rms-verdien for disse størrelsene. I resten av teksten er det underforstått at en snakker om effektivverdier av spenninger og strømmer, derfor skrives det bare U og I.

Når en sier at spenningen i en husholdning er 230 V er det effektivverdiene som oppgis. Toppverdien av spenningen finner en ved å multiplisere med $\scriptstyle {\sqrt {2}}$ noe som gir at toppverdien er 325 V.

Motstand for vekselstrøm i en resistans en spole eller en kondensator

Utdypende artikkel: Impedans

En generell vekselstrømskrets der Z er en impedans, V et voltmeter som måler spenningen over impedansen og I et amperemeter som måler strømmen i kretsen. Nederst er en veksel­spennings­kilde som gir sinus­formet spenning.

Innen vekselstrømsteknikk brukes begrepet impedans for motstand, denne deles inn i to størrelser, resistans og reaktans. Resistansen, eller ohmsk motstand, er det samme som i en likestrømskrets, mens reaktansen er en type motstand som gir spenningsfall over blant annet spoler og kondensatorer. En gir impedansen symbolet Z, resistansen symbolet R og reaktansen X. Alle disse størrelsene omtales i sammenheng med lineære kretselementer.

I motsetning til i likestrømskretser, vil spoler og kondensatorer være opphav til en spesiell type effekt som opptrer når de påtrykkes vekselspenning. Dette blir forklart lenger ned.

Resistans i en vekselstrømskrets

Om elementet Z, i kretsen over til høyre er en motstand med en gitt resistans R (Z = R), og spenningskilden gir en sinusformet vekselspenning vil det gå en sinusformet strøm gjennom kretsen. I henhold til Ohms lov vil det oppstå et spenningsfall over motstanden, som funksjon av tiden vil denne bli:

$u=Z{\hat {\imath }}\cos \omega t$

Spenningen og strømmen er begge proporsjonal med $\cos \omega t$ Relasjonen mellom strøm og spenning er den samme som i en likestrømkrets. Brukes effektivverdier kan spenningen over en ohmsk motstand skrives:

$U_{R}=IR$

Her brukes det altså store bokstaver, for selv om størrelsene er tidsvariable er det effektivverdiene som anvendes.

Induktans i en vekselstrømskrets – induktiv reaktans

Eksempel på små spoler til bruk i elektroniske apparater.

Symbolet for en spole.

Elementet Z i kretsen over til høyre kan byttes ut med en spole, også kalt reaktor, som forutsettes å være ideell, altså at den er uten ohmsk motstand. En spole representerer induktans i en elektrisk krets. Dette er egentlig en egenskap med alle elektriske ledere og har sammenheng med det magnetiske feltet som en elektrisk strøm fører med seg. For å forsterke denne effekten brukes det ofte en vikling med mange vindinger, omtrent som sytråd på en trådsnelle. Vindingene er isolert fra hverandre ved at lederne er dekket av et isolerende materiale, vindingene selv er typisk laget av tynn koppertråd. Settes det en kjerne av jern i senter av spolen økes induktansen ytterligere.

I henhold til Faradays lov vil det generelt oppstå en indusert spenning i spolen om strømmen gjennom den varierer:

$u={\frac {d\Phi }{dt}}=L{\frac {di}{dt}}$

Når det nå settes på en sinusformet spenning vil det igjen gå en sinusformet strøm i kretsen, og spolen vil reagere med å sette opp en spenning som er motsatt rettet av strømretningen gjennom den. Med matematisk utledning fremkommer dette uttrykket:

$u={\hat {\imath }}\omega L\cos(\omega t+{\frac {\pi }{2}})$

der L er induktansen i spolen med måleenheten Henry (H).

Det vil oppstå en motindusert spenning i spolen når den sinusformede strømmen har sin økning. Motsatt vil indusert spenningen motsette seg en minking av strømmen. Dette kalles for selvinduksjon, selvinduktans eller bare induktans. I formelen er vinkelen 90º et uttrykk for at strømmen er etter spenningen. Det er alltid vanlig å bruke spenningen som referanse.

Brukes effektivverdier for strøm og spenning kan uttrykket over skrives uten tilknytning til den trigonometriske funksjonen, slik at spenningsfallet over en spole skrives:

$V_{L}=I\omega L$

Begrepet induktiv reaktans defineres som X_L = ω L, da kan spenningsfallet skrives slik:

$V_{L}=IX_{L}$

Enheten for reaktans er ohm (Ω), det samme som for ohmsk motstand.

Kapasitans i en vekselstrømskrets – kapasitiv reaktans

Eksempel på små konden­satorer til bruk i elektroniske apparater.

Symbolet for en kondensator.

Om det i kretsen over til høyre settes inn en kondensator med kapasitans C med måleenhet Farad (F) vil det gå en strøm i kretsen når det påtrykkes en vekselspenning. Forholdet mellom strøm i og ladning Q er gitt av selve definisjonen av kapasitans:

$i={\frac {dQ}{dt}}=C\ {\frac {du}{dt}}$

Dersom den påtrykte sinusformede spenningen fører til en sinusformet strøm, vil perioden med stigende strøm gi en oppbygging av elektrisk ladning i kondensatoren. Det motsatt skjer når strømmen faller. Dermed er strømmen gjennom en kondensator proporsjonal hastigheten av endringen av spenningen over den. (I en spole er det spenningen som er proporsjonal med hastigheten av endringen strømmen.)

Ved matematisk utregning fremkommer dette uttrykket for spenning over en kondensator:

$v_{C}={\frac {I}{\omega C}}\cos(\omega t-{\frac {\pi }{2}})\,$

som altså sier at momentanverdien av strømmen er proporsjonal med endring av ladningen og med endringen av spenningen. Subtraksjonen av ${\frac {\pi }{2}}$, tilsvarende en vinkel på –90° gitt i radianer, sier at spenningen over en kondensator blir faseforskjøvet med en kvart periode. Dette kan også sies som at toppverdien av spenningen over kondensatoren oppstår 90° (altså ${\frac {\pi }{2}}$) etter at strømmen har sin toppverdi. Det er vanlig å definere dette som den fysiske størrelsen kapasitiv reaktans, som uttrykkes matematisk slik:

$X_{C}={\frac {1}{\omega C}}$

Og ved å bruke denne størrelsen og effektivverdier av strøm og spenning kan spenningen over en kondensator i en vekselstrømskrets skrives:

$V_{C}=IX_{C}$

Enheten for kapsitiv reaktans er ohm (Ω), det samme som for ohmsk motstand og induktiv reaktans. Kapasitiv reaktans er en egenskap med kondensatorer som får dem til å oppføre seg motsatt av spoler: En kondensator har en reaktans som er invers proporsjonal med størrelsen av kapasistansen og med frekvensen. Altså vil kondensatoren føre til en kortslutting om frekvensen gjøres høy nok.

Forholdet mellom impedans, resistans og reaktans

Triangel som viser forholdet mellom impedans, resistans og reaktans.

En vekselstrømskrets kan bestå av både resistans R, induktiv- og kapasitiv reaktans X, som sammen danner impedans Z. Forholdet mellom disse tre størrelsene uttrykkes slik:

$Z={\sqrt {R^{2}+X^{2}}}\,$

som er Pythagoras’ læresetning.

Momentan og effektivverdi av aktiv effekt

Momentan (rød kurve) og middel­effekt (Medeleffekt, sort stiplet strek) i et enfase­system. Legg merke til at kurven for momentan­effekten frem­kommer som produktet av spenning (sort) og strøm (blå) i kurvene over. Legg også merke til at arealet mellom x-aksen og middel­effekten er lik arealet mellom x-aksen og momentaneffekten.

Som tidligere nevnt er momentan effekt produktet av strøm og spenning. Formlene helt i innledningen av dette kapitlet anvendes, men det er nødvendig å ha en felles referanse for tiden t=0. En konvensjon er å la nullpunktet være det øyeblikket der strømmen passerer sitt positive maksimum. Ligningene for spenning og strøm kan da skrives:

$u(t)={\hat {u}}\cos(\omega t+\theta _{u}-\theta _{i})$

$i(t)={\hat {\imath }}\cos \omega t$

Med denne definisjonen blir momentan effekt:

$p=ui={\hat {u}}{\hat {\imath }}\cos(\omega t+\theta _{u}-\theta _{i})\cos \omega t$

I forbindelse med vekselstrøm er en interessert i å finne middelverdien av effekten. Dette er en verdi som er definert av følgende integral:

$P={\frac {1}{T}}\int _{t_{0}}^{t_{0}+T}p\,dt$

der T er periodetiden for sinusfunksjonen for strøm og spenning. Uttrykket for momentan effekt må integreres i formelen over, men det gir en enklere tolkning av resultatet om en først benytter følgende trigonometriske identitet på uttrykket for momentan effekt:

$\cos \alpha \cos \beta ={\frac {1}{2}}\cos(\alpha -\beta )+{\frac {1}{2}}\cos(\alpha +\beta )$

Her lar en α = ωt + θ_u - θ_i og β = ωt, dermed kan uttrykket for momentan effekt uttrykkes slik:

$p={\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})+{\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(2\omega t\theta _{u}+\theta _{u}-\theta _{i})$

Med å introdusere enda en trigonometrisk identitet, nemlig at:

$\cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta \,$

omformes det andre leddet på høyre side av effektligningen slik:

$p={\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})+{\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})\cos 2\omega t-{\frac {{\hat {u}}{\hat {\imath }}}{2}}\sin(\theta _{u}-\theta _{i})\sin 2\omega t\,$

som er formen en ønsker å få effektligningen på.

Så ved å sette dette inn i ligningen for definisjonen av effektivverdi av effekt fås:

${\begin{aligned}P&={\frac {1}{T}}\int _{t_{0}}^{t_{0}+T}pdt\\&={\frac {1}{T}}\int _{t_{0}}^{t_{0}+T}\left[{\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})+{\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})\cos 2\omega t-{\frac {{\hat {u}}{\hat {\imath }}}{2}}\sin(\theta _{u}-\theta _{i})\sin 2\omega t\right]dt\\&={\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})\end{aligned}}$

Effektivverdi av effekt er altså ikke tidsavhengig, men har en konstant verdi gitt av spenning, strøm og fasevinklene til hver av disse.

En fysisk tolkning av begrepet middeleffekt er at om en sinusformede vekselstrøm ble erstattet av sin ekvivalente likestrøm (effektivverdi), ville effektutviklingen i en ohmsk motstand bli den samme. Tilsvarende gjelder for en spenning og effektutvikling. Dette ble også nevnt lenger opp der effektivverdier av sinusformede vekselstrømmer og spenninger ble forklart.

Momentanverdier av sinusformet strøm, spenning og effekt i en rent ohmsk motstand. Legg merke til at sinuskurven for effekten får dobbelt så stor frekvens som strøm og spenning. Fordi både strøm og spenning til enhver tid er enten positiv eller negativ, blir momentanverdien av effekten alltid positiv.

For et ideelt tilfelle med en rent ohmsk motstand vil strøm og spenning være i fase, dermed vil θ_u = θ_i, og hele uttrykket over for momentan effekt kan reduseres slik:

$p={\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})+{\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})\cos 2\omega t\,$

fordi sinus til vinkelen 0° er 0. Ved å benytte uttrykket for aktiv effekt som en fant ved integrasjonen over kan uttrykket for momentaneffekt rett over forenkles ved innsetting:

$p=P+P\cos 2\omega t$

I figuren til høyre er momentanverdiene av strøm, spenning og effekt gitt for en rent ohmsk motstand. I figuren er også middelverdien av effekt P angitt som den brune horisontale streken. Her legger en merke til at momentaneffekten er en sinuskurve med dobbelt så stor frekvens som spenning og strøm. En legger også merke til momentaneffektens sinuskurve er positiv for hele sitt forløp (altså ligger over x-aksen).

At momentaneffekten for enfasesystemer er tidsavhengig har sine ulemper. For eksempel vil flere typer elektriske motorer for enfasestrøm ikke avgi jevn effekt på akslingen, noe som resulterer i momentpulseringer. Dette er grunne til at motoren i et kjøleskap vibrerer, og at den er montert på store gummidempere for at ikke hele kjøleskapet skal riste.

Den momentane effekten uttrykt i formelen over kalles for momentan aktiv effekt. Dette betyr igjen at middelverdien av effekten P refereres til som aktiv effekt. En bruker denne termen for å gjøre oppmerksom på at det er denne effekten som blir transformert fra elektrisk til ikke-elektrisk effekt. I tilfelle med et rent ohmsk nettverk blir avgitt effekt omformet til varme.

Momentan og effektivverdi av reaktiv effekt

Momentanverdier av strøm (current), spenning (voltage), momentan­effekt (power) og middel­effekt (Average Power) i en rent induktiv krets.

For tilfelle med et rent induktiv kretselement vil strømmen være bak spenningen med 90°^{[trenger referanse]} – i radianer ${\frac {\pi }{2}}$ – dermed vil vi ha:

$\theta _{i}=\theta _{i}-{\frac {\pi }{2}}\qquad \Rightarrow \qquad \theta _{u}-\theta _{i}={\frac {\pi }{2}}$.

Siden cosinus til 90° er lik null, vil uttrykket for momentan effekt reduseres til:

$p=-{\frac {{\hat {u}}{\hat {\imath }}}{2}}\sin 2\omega t$

I tilfellet med et rent kapasitivt kretselement vil strømmen være foran spenningen med 90°.^{[trenger referanse]} Altså vil vi ha

$\theta _{i}=\theta _{i}+{\frac {\pi }{2}}\qquad \Rightarrow \qquad \theta _{u}-\theta _{i}=-{\frac {\pi }{2}}$.

Dermed kan momentan effekt for en slik rent kapasitiv krets uttrykkes:

$p={\frac {{\hat {u}}{\hat {\imath }}}{2}}\sin 2\omega t$

Effekten som er relatert til induktans og kapasitans kalles for reaktiv effekt. Om en ser på ligningen et stykke opp for momentan effekt er koeffisienten foran leddet sin 2ωt definert til å være middelverdien av reaktive effekten Q, altså:

$Q={\frac {{\hat {u}}{\hat {\imath }}}{2}}\sin(\theta _{u}-\theta _{i})$

I figuren over til høyre er den momentane strømmen, spenningen og effekten til en rent induktiv krets vist. Igjen ser en at frekvensen til den momentane effekten med lilla farge har dobbelt så stor frekvens som strøm og spenning. En annen ting er at middelverdien av effekt, som er vist med brun strek i figuren, er lik null. For en rent kapasitiv krets vil også middelverdien av effekt være lik null. Det betyr at i en rent induktiv eller kapasitiv krets vil det ikke være noen overgang fra elektrisk effekt til ikke-elektrisk effekt.

Momentan og effektivverdi av aktiv- og reaktiv effekt

Momentanverdier av strøm (current), spenning (voltage) og effekt (power) i en krets som kan bestå av både en eller flere resistorer, spoler og konden­satorer, eller bare resistorer og spoler.

I en krets som er sammensatt av resistans, kapasitans og induktans, med større eller mindre grad av disse tre elementene, vil strøm og spenning være faseforskjøvet mindre enn 90°. I figuren til høyre er sinusformet strøm og spenning vist der θ_u = 90° og θ_i = 45°, slik at faseforskyvningen tyder på at kretsen totalt sett er induktiv. Dette fordi strøm er foran spenningen.

Legg merke til at momentan effekt, merket med lilla farge, stort sett er positiv, og at middelverdien av effekt alltid er positiv. I et passivt nettverk, altså en krets uten spenningskilder, betyr negative verdier av momentan effekt at energi blir lagret i kondensatorer og spoler. At momentaneffekten har negative verdier i kortere eller lengre perioder betyr at i disse tidsintervallene finnes det komponenter som kan levere energi til den øvrige delen av kretsen. Om det for eksempel er en kondensator i kretsen vil den ta imot elektrisk energi når den lades opp. Den samme energien avgis ved utladning. Oppladning og utlading skjer i henholdsvis perioden der vekselspenningen har økende verdi og minkende verdi, altså meget hurtig. Om det er en spole som er årsak til energilagring og avgivelse har det sammenheng med at magnetfeltet bygger seg henholdsvis opp og ned, altså det som over ble definert som induksjon. Imidlertid vil lagring av energi i en spole skje når det er strømmen som øker i henhold til sinusfunksjonen. Nedbygging av magnetfeltet og avgivelse av energi skjer ved minkende strøm. I kondensatoren har altså lagring av energi sammenheng med opp og nedbygging av et elektrisk felt, mens det i spolen har sammenheng med et magnetisk felt. Sagt på en annen måte har reaktiv effekt sammenheng med energiomsetning i elektriske- og magnetiske felter.

I avsnitt over ble reaktiv effekt definert. Sammen med uttrykket for middelverdien av aktiv effekt, som gjentas her:

$P={\frac {{\hat {u}}{\hat {\imath }}}{2}}\cos(\theta _{u}-\theta _{i})\,$

kan hele uttrykket for momentan effekt uttrykkes ved hjelp av middelverdien av aktiv- og reaktiv effekt, slik:

$p=P+P\cos 2\omega t-Q\sin 2\omega t$

Hensikten med å benytte de forskjellige trigonometriske identitetene i utledningen over var å få satt opp denne enkle formelen.

Effektfaktor eller cos φ

Bærbart måle­instrument for effekt­faktor. Skalaen viser effekt­faktoren med klar indikering for om den måler induktive- (merket «IND.») og kapasitive verdier (merket «CAP.»).

Med valget om at strømmen som referanse sier en at reaktiv effekt Q er positiv for spoler (induktans) og negativ for kondensatorer (kapasitans). En sier også at spoler tar opp reaktiv effekt, mens kondensatorer produserer reaktiv effekt.

Fasevinkelen for spenning ble definert $\theta _{u}$ og for strøm $\theta _{i}$. Imidlertid er det mer vanlig å kun betrakte differansen mellom disse to vinklene og kalle den for $\varphi$. Vi definerer altså $\varphi =\theta _{u}-\theta _{i}$. Videre er effektfaktoren, eller bare $\cos \varphi$ som en ofte sier, definert slik:^{[trenger referanse]}

$\cos \varphi =\cos(\theta _{u}-\theta _{i})$

I figuren til over til høyre er den relative faseforskyvningen rundt 45° og effektfaktoren blir da 0,707.

For å gjøre forskjell på induktiv og kapasitiv effektfaktor kunne en ha brukt fortegn, men misforståelser unngås om en heller skriver «cos φ = 0,7 kapasitiv» eller «cos φ = 0,9 induktiv». Se illustrasjonen til høyre som viser et instrument for å måle effektfaktoren der måleskalaen har nettopp slike angivelser.

Med effektfaktoren definert kan middelverdien av aktiv effekt bestemmes med denne formelen:

$P=\cos \varphi IU$

Om en elektrisk krets er rent ohmsk vil $\cos \varphi =1$, all effekt er da aktiv.

Sinus til vinkelen $\varphi$ er assosiert med reaktiv effekt, dermed kan en finne middelverdien av reaktiv effekt slik:

$Q=\sin \varphi IU$

I en krets som er rent kapasitiv eller induktiv vil $\cos \varphi =0$ (effektfaktor lik null) og $\sin \varphi =1$. For en reaktiv krets skal dette godt gjøres, for eksempel vil en spole ha noe ohmsk motstand. Om en spole har jernkjerne vil det oppstå såkalt hysteresetap og virvelstrømstap i jernet. Dette medfører varmeutvikling, slik at kretsen må tilføres noe aktiv effekt. For øvrig vil det i en seriekoblet krets med resistans, induktans og kapasitans være slik at $\cos \varphi =R/Z$.

Automatisk fase­kompensering for industri­formål. De seks blanke sylinderne er kondensatorer av forskjellig størrelse. Ved å koble inn og ut kondensatorene kan effekt­faktoren holdes nærmest mulig 1. En egen regulator sørger for at dette skjer automatisk, selv om for eksempel elektriske motorer stadig endrer belastnings­grad. Med fase­kompensering sørger en for at reaktiv effekt overføres over korte avstander, istedenfor å trans­porteres hele veien mellom kraft­stasjoner og forbrukere.

I et elektrisk kraftsystem er lav effektfaktor, altså $\cos \varphi$ mindre enn 1, en uønsket egenskap. Årsaken til dette er at for en gitt spenning må en større strøm til for å overføre ønsket effekt. Dette vil igjen føre til at de ohmsk tapene i kraftlinjene og andre komponenter som er proporsjonale med $I^{2}R$ øker. Med andre ord fører lav effektfaktor til økte overføringstap. På grunn av dette er det vanlig at kraftselskapene tar ekstra betaling fra abonnementer med lav effektfaktor. Typisk er det slik at elektriske motorer trekker reaktiv effekt. For å unngå at denne reaktive effekten skal overføres over kraftnettet er det mulig å kompensere denne med kondensatorer. Tilpasses denne til en eller flere elektriske apparater med ugunstig effektfaktor kan resultatet bli at det ikke overføres reaktiv effekt. Eller sakt på en annen måte tilstrebes effektfaktor lik 1. En kaller slike tiltak for fasekompensering. Bildet til høyre viser en automatisk fasekompensator for industriformål.

På samme måte som aktiv effekt assosieres med ohmsk motstand, der enkle formler brukes for å finne sammenheng mellom effekt og resistans, finnes lignende sammenhenger for reaktans og reaktiv effekt. Om reaktansen X er kjent kan en finne reaktiv effekt Q ved denne sammenhengen:^{[trenger referanse]}

$Q=UI=I^{2}X={U^{2} \over X}\,$

som altså har samme form som formlene for resistorer.

Tilsynelatende effekt

Diagram som viser forholdet mellom aktiv-, reaktiv- og tilsyne­latende effekt. I den rett­vinklede trekanten er tilsyne­latende effekt hypotenus og de andre to størrelsene kateter, dermed benyttes Pythagoras’ læresetning for å bestemme størrelsen av dem.

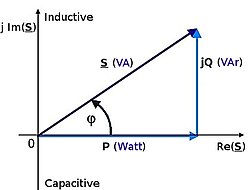
En annen viktig størrelse er syneffekten som er produktet av spenning og strøm:^{[trenger referanse]}

$S={\frac {{\hat {v}}{\hat {\imath }}}{2}}$

eller om det brukes effektivverdier:

$S=UI$

Lenger opp ble det vist at formelen for aktiv effekt utviklet i en motstand P hadde samme form. Det vil altså si at i en rent ohmsk krets er S = P. Derimot i en sammensatt krets av alle de tre typene elektrisk effekt vil sammenhengen være slik:

$S={\sqrt {P^{2}+Q^{2}}}$

Når effekten for en elektrisk maskin oppgis, for eksempel en transformator, generator, elektrisk motor eller reaktor snakker en gjerne om tilsynelatende effekt S med måleenheten voltampere (VA). Når en snakker om omsatt nyttiggjort effekt i en elektrisk motor, altså effekten ut på akslingen, er det vanlig å bruke aktiv effekt P (W). Det samme gjelder for en lyspære eller en varmeovn. Om en oppgir effekten for en spole eller en kondensator bruker en enheten (VAr) der r er en forkortelse for reaktiv.^{[trenger referanse]}

Tilsynelatende effekt kan en finne for et kretselement der impedansen Z er kjent slik:

$S=I^{2}Z={U^{2} \over Z}\,$

der det forutsettes at I og U er effektverdier. For øvrig er det så vanlig at S, P og Q er middelverdier at det tas for gitt.

Effekt i trefasekretser

Utdypende artikkel: Trefase

For å få en forståelse av effektutvikling i trefasekretser er det nødvendig med en beskrivelse av begreper og konsepter innenfor denne delen av elektroteknikken.

Strøm og spenning i trefaskretser

De tre sinus­kurvene som danner trefase veksel­spenning eller strøm. Langs x-aksen er det angitt grad­tallet, men dette kunne også vært tiden. I et kraft­system med 50 Hz vil hver av kurvene gjennom­løpe én hele periode i løpet av 20 ms. 360° tilsvarer da tiden 20 ms. Langs y-aksen vil en ha spenning eller strøm.

Trefasesystemet har vært praktisk talt enerådende etter at det ble introdusert ved den internasjonale elektrotekniske utstillingen i 1891 i Frankfurt am Main i Tyskland. Det er flere grunner til det, noen av de viktigste årsakene er at:

• en trefaset motor eller generator vil ha mindre volum og vekt enn en tilsvarende maskin for enfasestrøm,
• for å overføre denne samme effektmengden i en kraftlinje vil det kreves mindre samlet ledertverrsnitt for trefase- enn for enfasestrøm,
• at trefasesystemet gir et roterende magnetfelt i motorer noe som gjør at de blant annet blir selvstartende.

Spesielle tiltak gjøres for å få enkelte motortyper for enfase til å starte å rotere når de tilkobles spenning.

I et trefasesystem er det tre faseledere istedenfor to som i enfasesystem behandlet over. Disse lederne må tilknyttes generatorer spesielt for trefasestrøm, som en kan tenke seg som tre spenningskilder som hver gir ut vekselspenning med samme størrelse, altså lik frekvens og amplitude.^{[trenger referanse]} Imidlertid er de tre fasespenningene faseforskjøvet med nøyaktig 120°, eller $2\pi /3$ radianer. Ideell syklisk symmetrisk sinusformet trefase spenning eller strøm er vist i figuren øverst til høyre. Generelt beskrives de tre spenningene av følgende trigonometriske funksjoner:

$u_{L1}={\hat {u}}_{L1}\cos(\omega t)$

$u_{L2}={\hat {u}}_{L2}\cos(\omega t-{\frac {2\pi }{3}})$

$u_{L3}={\hat {u}}_{L3}\cos(\omega t+{\frac {2\pi }{3}})$

Der symbolene er de samme som tidligere, og L1, L2 og L3 tilsvarer fasene henholdsvis 1, 2 og 3 i figuren. Det er for øvrig vanlig å betrakte spenningene som såkalte fasevektorer, men dette konseptet blir ikke omtalt her. At de tre fasene er forskjøvet med 120° vil også si at det er en tidsforskyvning av det tre sinuskurvene. Om frekvensen er 50 Hz vil faseforskyvningen være 6,667 ms mellom hver av spenningene eller strømmene. Også strømmen som går i et trefasesystem vil være symmetrisk og beskrives av de samme formlene som over, forutsatt at belastningen er symmetrisk.

En trefaset generator koblet i stjerne (venstre) og en last også koblet i stjerne.

En trefaset generator koblet i stjerne (venstre) og en last koblet i trekant.

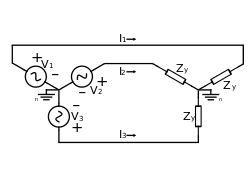
Figuren til høyre viser et prinsipielt trefasesystem med tre spenningskilder V₁, V₂ og V₃ til venstre i figuren og tre belastninger Z_y til høyre. Belastning kan være kombinasjoner av resistorer, spoler og kondensatorer, og det forutsettes at disse er like. Denne sammenkoblingen av spenningskildene og de tre belastningene kalles for stjernekobling. Med stjernekobling er det et fellespunkt for spenningskildene og belastningene som kalles nøytralpunkt. Nøytralpunktet kjennetegnes med at spenningen er null. I figuren nederst til høyre er det vist det samme skjemaet, men her er lastene satt sammen på en måte som kalles trekantkobling. Dermed er impedansene for belastningen merket Z_∆^{[trenger referanse]}

Med de tre belastningene i stjernekobling vil strømmen inn til hver av impedansene være den samme som strømmen som går i faselederen hver av dem er tilknyttet. Derimot vil strømmen inn til lastene med trekantkobling ikke lenger være den samme. Forholdet mellom strøm i faselederne og i hver av impedansene er gitt av denne sammenhengen:

$I_{1}={\sqrt {3}}I_{12},$

$I_{2}={\sqrt {3}}I_{23},$

$I_{3}={\sqrt {3}}I_{31},$

Der en kaller $I_{1}$, $I_{2}$ og $I_{3}$ for linjestrømmer, og $I_{12}$, $I_{23}$ og $I_{31}$ for fasestrømmer.

For øvrig er det også vanlig å benevne fasestrømmene med bokstaven $\phi$, slik at fasestrømmene over kun benevnes $I_{\phi }$.

De tre linje­spenningene og fase­spenningene i et kraft­system med 400 V. Amplituden for linje­spenningene er ${\sqrt {2}}$ ganger større enn linje­spenningen, altså 565 V. Det samme gjelder fase­spenningenes amplitude­verdi på 325 V. Fase­spenningene er ${\sqrt {3}}$ mindre enn linje­spenningene, mens det er en fase­forskyvning mellom dem på 30°.

For spenningene i stjernekoblingen i figuren øverst er størrelsen for linjespenninger og fasespenninger forskjellige. Linjespenningene defineres som spenningen mellom hver av de tre faselederne, mens fasespenningene er spenningene mellom hver av faselederne og nøytralpunktene. Linjespenningene ble over kalt U_L1, U_L2 og U_L3, men fra nå av kalles diss U₁₂, U₂₃ og U₃₁. Fasespenningene kalles U_1n, U_2n og U_3n. Forholdet mellom linje- og fasespenninger er:

$U_{12}={\sqrt {3}}U_{1n},$

$U_{23}={\sqrt {3}}U_{2n},$

$U_{31}={\sqrt {3}}U_{3n},$

Det betyr altså at linjespenningene er $\scriptstyle {\sqrt {3}}\approx 1,73$ større enn fasespenningene.

For øvrig er det vanlig i litteraturen å benevne fasespenning som $U_{\phi }$, og andre faseverdier som impedans $Z_{\phi }$, effekt $P_{\phi }$ og reaktiv effekt $Q_{\phi }$ når sammenhenger i trefasesystemet skal utledes matematisk.

Middelverdien av effekt i trefasekretser

For impedans 1, altså den som tilføres strømmen I₁ i de stjernekoblede lastene Z_y i figuren over er utviklet middeleffekt uttrykt ved effektivverdiene (rms) av spenning og strøm:

$P_{1}=U_{1n}I_{1}\cos(\theta _{u1}-\theta _{i1}),$

der θ_u1 og θ_i1 er fasevinklene til henholdsvis spenning og strøm. Videre uttrykkes effekten for de to andre belastningene med samme notasjon for fasevinklene:

$P_{2}=U_{2n}I_{2}\cos(\theta _{u2}-\theta _{i2}),$

$P_{3}=U_{2n}I_{2}\cos(\theta _{u3}-\theta _{i3}),$

I en syklisk symmetrisk trefasekrets med like stor impedans for hver av lastene vil alle fasespenningene og strømmene være like, altså gjelder:

$U_{\phi }=U_{1n}=U_{2n}=U_{3n},$

$I_{\phi }=I_{1n}=I_{2n}=I_{3n},$

og dessuten:

$\theta _{\phi }=\theta _{u1}-\theta _{i1}=\theta _{u2}-\theta _{i2}=\theta _{u3}-\theta _{i3}$

Middelverdien av effekt per fase må i dette syklisk symmetriske og balanserte trefasesystemet være identiske, altså:

$P_{\phi }=P_{1}=P_{2}=P_{3}=U_{\phi }I_{\phi }\cos \theta _{\phi }$

Den totale middelverdien av effekten for alle lastene blir dermed:

$P_{T}=3P_{\phi }=3U_{\phi }I_{\phi }\cos \theta _{\phi }$

Det vil også være ønskelig å uttrykke den totale middelverdien av effekten som effektivverdien av linjespenning og linjestrøm. Siden alle linjespenningene i absoluttverdi er like kan en kalle linjepenningene for U og tilsvarende linjestrømmene for I, dermed kan uttrykket over omformes slik:

$P_{T}=3\left({\frac {U}{\sqrt {3}}}\right)I\cos \theta _{\phi }={\sqrt {3}}UI\cos \theta _{\phi }$

På samme måte gjelder det for reaktiv effekt at effektivverdi av effekt i én av lastene er:

$Q_{\phi }=U_{\phi }I_{\phi }\sin \theta _{\phi },$

og for den totale reaktive effekten uttrykt med linjespenning og -strøm:

$Q_{T}=3Q_{\phi }={\sqrt {3}}UI\sin \theta _{\phi }$

Dessuten gjelder for tilsynelatende effekten at:

$S_{T}=3S_{\phi }={\sqrt {3}}UI$

For en trekantkoblet last gjelder på samme måte at effekten i hver av impedansene kan uttrykkes:

$P_{1}=U_{12}I_{12}\cos(\theta _{u12}-\theta _{i12}),$

$P_{2}=U_{23}I_{23}\cos(\theta _{u23}-\theta _{i23}),$

$P_{3}=U_{31}I_{31}\cos(\theta _{u31}-\theta _{i31}).$

Belastningen er balansert og spenningskildene syklisk symmetriske, dermed gjelder at:

$U_{\phi }=U_{12}=U_{23}=U_{31}\,$

$I_{\phi }=I_{12}=I_{23}=I_{13}\,$

og dessuten:

$\theta _{\phi }=\theta _{u12}-\theta _{i12}=\theta _{u23}-\theta _{i23}=\theta _{u13}-\theta _{i13}$

Middelverdien av effekt per fase i trekantkoblingen i det balanserte systemet må være identiske, altså gjelder:

$P_{\phi }=P_{1}=P_{2}=P_{3}=U_{\phi }I{\phi }\cos \theta _{\phi }$

Den totale middelverdien av effekten for hele lasten blir dermed:

$P_{T}=3P_{\phi }=3U_{\phi }I_{\phi }\cos \theta _{\phi }$

Og for effekten uttrykt ved hjelp av linjespenning og linjestrøm:

$P_{T}=3I\left({\frac {I}{\sqrt {3}}}\right)\cos \theta _{\phi }={\sqrt {3}}UI\cos \theta _{\phi }$

Altså akkurat samme formel som for de stjernekoblede belastningene. Når det gjelder total reaktiv effekt Q_T og tilsynelatende effekt S_T gjelder også de samme formlene som for den stjernekoblede belastningen. For øvrig er det som nevnt vanligere å benyttet symbolet φ for fasevinkel istedenfor θ_ϕ.

En spesiell sammenheng for stjerne og trekantkoblede laster er at totaleffekten i trekantkobling er tre ganger så stor som effekt som utvikles om de samme impedansene var koble i stjerne. Dette utnyttes i trefase asynkronmotorer der en ønsker å begrense startstrømmen. Først kobles spenningen til motoren med viklingene i stjernekobling. Etter at motoren har fått normalt turtall kobles vindingene over i trekant. Systemet for slik omkobling kalles for en stjerne/trekant-vender.

Momentan effekt i trefasekretser

At momentan­effekten til enhver tid er konstant i et tre­fase­system gjør at asynkron­motorer som denne får et jevnt moment på akslingen. Rotoren i midten som er tilknyttet akslingen settes i rotasjon på grunn av det roterende magnet­feltet som skapes av statoren. Statoren er her skåret delvis over, men noe av stator­viklingene kan sees. For øvrig er det viklingene i statoren som er tilknyttet kraft­systemet, og som ved tilførsel av tre­fase­strøm skaper det resulterende roterende magnetfeltet.

Den momentane effekten i en trefaselast kan uttrykkes for hver av de tre impedansene uttrykkes slik:

$p_{1}={\hat {u}}_{1n}{\hat {\imath }}_{1}={\hat {u}}_{\phi }{\hat {\imath }}_{\phi }\cos \omega t\cos(\omega t-\theta _{\phi }),$

$p_{2}={\hat {u}}_{2n}{\hat {\imath }}_{2}={\hat {u}}_{\phi }{\hat {\imath }}_{\phi }\cos(\omega t-{\frac {2\pi }{3}})\cos(\omega t-\theta _{\phi }-{\frac {2\pi }{3}}),$

$p_{3}={\hat {u}}_{3n}{\hat {\imath }}_{3}={\hat {u}}_{\phi }{\hat {\imath }}_{\phi }\cos(\omega t+{\frac {2\pi }{3}})\cos(\omega t-\theta _{\phi }+{\frac {2\pi }{3}}),$

Her er det benyttet amplitudeverdier for spenning og strøm for fasespenninger og -strømmer. Ved bruk av trigonometriske identiteter utledes dette slik at summen av effekten for hver av fasene blir:

$p_{T}=p_{1}+p_{2}+p_{3}=1,5{\hat {u}}_{\phi }{\hat {\imath }}_{\phi }\cos \theta _{\phi }$

Dette kan også uttrykkes med effektivverdier for fasestrøm og -spenning:

$p_{T}=3U_{\phi }I_{\phi }\cos \theta _{\phi }$

Altså er momentaneffekten i en belastning med trefasestrøm en konstant størrelse, altså uavhengig av tiden som i et enfasesystem. Dette er en av de viktigste egenskapene med et trefasesystem og er grunnen til at en trefasemotor utvikler et jevnt moment ut på akslingen. Dette i motsetning til en enfasemotor som vil kunne vibrere.

Eksempel på beregning av effekt for en vekselstrømskrets

Hver generator i kraftstasjonen tilknyttet de tre kløfters demning har en maksimal effekt på 840 MVA, effektfaktoren er oppgitt til 0,9 og linjespenningen er på 20 kV. Hvor stor er linjestrømmen? Hvor mye aktiv- og reaktiv effekt produserer generatoren? Hvor stor er årlig energiproduksjon med forutsetning om at generatoren går med denne ytelsen hele året?

For å regne ut strømmen må en benytte formelen for trefase tilsynelatende effekt løses med hensyn på strøm:

$I={\frac {S_{T}}{{\sqrt {3}}U}}={\frac {840\cdot 10^{6}\ MVA}{{\sqrt {3}}\cdot 20\cdot 10^{3}\ V}}=24249\ A$

Strømmen og de andre opplysningene benyttes videre for å finne aktiv og reaktiv effekt:

$P_{T}={\sqrt {3}}UI\cos \theta _{\theta }={\sqrt {3}}\cdot 20\cdot 10^{3}\ V\cdot 24,2\cdot 10^{3}\ A\cdot 0,9=756,0\ MW$

Med effektfaktoren 0,9 vil det si at cos φ = 0,9 der φ = arcuscosinus 0,9 = 25,84°. Denne vinkelen må en kjenne for å finne sin φ, som i dette tilfellet blir lik 0,44.

$Q_{T}={\sqrt {3}}UI\sin \theta _{\theta }={\sqrt {3}}\cdot 20\cdot 10^{3}\ V\cdot 24,2\cdot 10^{3}\ A\cdot 0,44=368,9\ MVAr$

En test for å se om regnestykkene ble riktige er å kontrollere om aktiv og reaktiv effekt tilsammen gir tilsynelatende effekt. Til dette brukes den pytagoreiske læresetning:

$S_{T}={\sqrt {P^{2}+Q^{2}}}={\sqrt {(756,0^{2}+368,9^{2})\cdot 10^{6}}}\approx 840\ MVA$

Som stemmer overens med de oppgitte opplysningene.

Årlig energiproduksjon i MWh er produktet av effekt og tiden. I et år er det 365 dager, med 24 timer i døgnet blir det total 8760 timer i året. Dermed blir energiproduksjonen:

$W=PT=756\cdot 10^{6}\ W\cdot 8760\ h=6\ 622\ 560\ MWh=6,6\ TWh$

Måling av elektrisk effekt

Merkeplaten på et enfase wattmeter viser hvordan tilkoblingen skal gjøres. Legg merke til at referanse for tilkobling er energi­kilde (Source) og belastning (Load).

For å måle effekt brukes et wattmeter som i sin enkleste form er et viserinstrument. Det har to spoler for måling der den ene spolen kalles strømspolen og er stasjonær. Den andre spolen kalles spenningsspolen og er bevegelig, til denne er selve viseren festet. Viseren angir effekten på en skala som kan avleses. Strømspolen er konstruert for å måle en strøm som er proporsjonal med laststrømmen, mens spenningsspolen er laget for å måle en strøm som er proporsjonal med spenningen. Gjennomsnittlig utslag av viseren er proporsjonal med effektivverdien av spenningen gjennom spenningsspolen, effektivverdien av strømmen gjennom strømspolen og effektfaktoren (cos φ) til fasevinklen for strøm og spenning. For at wattmetret skal kunne måle riktig er tilkoblingen til ledningene viktig, noe som er illustrert i figuren til høyre.

For å måle effekten til en trefaselast er to-wattmetermetoden et grunnlegende konsept. Dette går ut på at to wattmetre må brukes for å måle effekt for en symmetrisk last. Total effekt er da summen av effekten målt i de to wattmetrene.

Størrelsen av effekt i forskjellige sammenhenger

Som eksempel på liten elektrisk effekt i elektriske apparater kan det nevnes at elektroniske hjelpemidler som klokker, lommekalkulatorer og mobiltelefoner typisk yter noe få watt. Andre små apparater som radio eller en moderne sparepærer yter bare noen titalls watt. Elektriske apparater i husholdningen har gjerne en effekt på noen hundre watt, som for eksempel en miksmaster, en datamaskin, en fryser eller et kjøleskap. En elektrisk komfyr, vaskemaskin, eller tørketrommel har betydelig større ytelse, gjerne noen kW.

Når det gjeler store ytelser for industrielle anvendelser finnes det serieproduserte elektriske motorer på ytelser opp mot 100 000 hk, eller rundt 73 MW. En elektrisk generator som etter planen skal settes i drift i et atomkraftverk i Finland i 2018 skal ha en ytelse på hele 2000 MVA. Verdens desidert største kraftverk er det i tilknyttet de tre kløfters demning med en total ytelse på hele 22 500 MW.

Se også

• Amperetime
• kWh/h
• Fotoelektrisk effekt
• Effektiv energibruk
• Overføringsnett

Noter

Type nummerering

Litteratur

• Hallseth, Haugan, Hjelmen og Isnes (1990). Fysikk for ingeniører (på norsk) (1 utg.). NKI Forlaget. ISBN 82-562-2068-6. CS1-vedlikehold: Flere navn: forfatterliste (link)

• Sigurd Stensholdt (1974). Fysikk PSSE (på norsk). 3 – Elektrisitet (1 utg.). Universitetsforlaget. ISBN 82-00-25342-2.  [Yrkesopplæringsrådet for håndverk og industri]

• Hugo D. Young og Roger A. Freedman (2008). University Physics (på engelsk) (XII utg.). Addison Wesley. ISBN 978-0-321-50130-1. 

• James W. Nilsson (1990). Electric Circuits (på engelsk) (tredje utg.). Ames, Iowa: Addison-Wesley. ISBN 0-201-51036-7. 

• A. E. Fitzgerald, Charles Kingsley, Jr. Og Stephen D. Umans (1992). Electric machinery (Fifth Edition in SI units utg.). McGraw-Hill Book Co. ISBN 0-07-707708-3. CS1-vedlikehold: Flere navn: forfatterliste (link)

Eksterne lenker

• Basalt om effekt og energi fra US department of energy
• Basalt om elektrisk effekt
• Side som forklarer forskjellen på momentan, gjennomsnittlig, aktiv og reaktiv effekt