Voltmeter
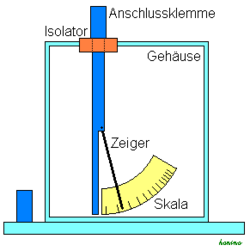

Et voltmeter er et apparat som brukes til å måle elektrisk spenning som angis i SI-enheten volt.
Likespenning[rediger | rediger kilde]
Det enkleste voltmeteret måler høyere spenninger og kalles et elektroskop hvis det bare indikerer at en spenning er til stede, eller et elektrometer hvis det også har en skala for avlesning. Funksjonen baserer seg på at like ladninger frastøter hverandre. Spenningen tilføres en metallstav som det er festet en viser til. Viseren er svært lett og blir utsatt for en kraft som stiger ulineært med den ladningen som spenningen setter opp på både stav og viser. Motkraften er jordas tyngdekraft. Elektroskopet trenger ingen målestrøm ettersom det arbeider rent kapasitivt. Referansen (den andre polen) kobles til et ledende hus med vindu som omslutter staven, som selv er isolert fra huset. Elektroskopet angir ikke spenningens polaritet.
Et annet enkelt voltmeter baserer seg på et potensiometer i en målebro. En kjent spenning tilføres potentiometret, som består av en motstand med et fritt innstillbart tappepunkt. Spenningen fra tappepunktet sammenlignes med den ukjente spenningen ved hjelp av en nulldetektor i målebroen. Tappepunktet flyttes slik at brospenningen blir 0 V, og ut fra tappepunktets posisjon kan spenningen beregnes. Den kjente spenningen må være høyere enn målespenningen. Nulldetektoren forstyrrer ikke målingen siden det går null strøm gjennom den ved avlesning.

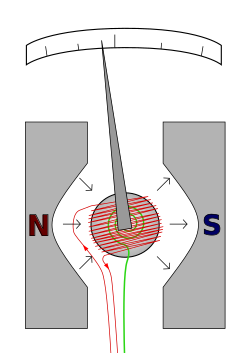

Et annet svært praktisk voltmeter baserer seg på dreiespoleinstrumentet, som i prinsippet er en strømmåler (fordi strømmen genererer magnetfeltet som flytter viseren). Motkraften kommer fra en spiralfjær. For å måle høyere spenninger settes en motstand med passende verdi i serie med dreiespoleinstrumentet. Når motstandsverdien er kjent, kan spenningen leses av som utslaget på dreieinstrumentet. Skalaen er da tilpasset seriemotstandens verdi. Fordi dreiespolen er utsatt for et kraftig konstant magnetfelt, blir strømretningen også vist.
Et annet viserinstrument er dreiejerninstrumentet, som baserer seg på reluktanskraften mellom to jernbiter plassert i en spole. Den ene biten er koplet til viseren (rotor) og den andre er fast (stator).Siden begge polariteter av påtrykket frastøter jernbitene, kan dette instrumentet også brukes til måling av vekselspenning uten bruk av en likeretter. Kraften til viseren er proporsjonal med kvadratet av strømmen, noe som gjør skalaen ulinjær. Ulinjæriteten kan forbedres ved å forandre den mekaniske formen på rotor og stator. Instrumentet egner seg spesielt godt til måling av svært sterke strømmer, da spolen ligger utenfor visersystemet.
Et dreiespoleinstrument som er modifisert slik at permanentmagneten er erstattet av en elektromagnet som også (i tillegg til dreiespolen) magnetiseres av målestrømmen, vil som dreiejerninstrumentet få en kvadratisk skala, og begge polariteter på tilkoplingene vil gi positivt utslag. Instrumentet betegnes da elektrodynamisk. For vekselspenning trengs heller ingen likeretter.
Voltmeter er også ett av instrumentene som inngår i et digitalt multimeter, som vist på bildet. Det finnes også digitale voltmetre uten andre oppgaver.
De galvanometriske voltmetere (dreiejern, dreiespole, elektrodynamisk) trenger noe kraft for å flytte viseren. Denne kraften tas fra kilden til spenningen som skal måles og belaster den, slik at målespenningen kan synke noe i absolutt verdi ved målingen, avhengig av målepunktets indre resistans, eller kilderesistans.
For voltmetere som baserer seg på dreiespoleinstrumentet eller dreiejerninstrumetet, økes verdien til seriemotstanden for høyere måleområder. Målestrømmen for fullt utslag er alltid den samme, men blir oftest ikke angitt direkte. I stedet brukes den inverse verdien Ohm per Volt (per Volt full-skala er underforstått) for å karakterisere instrumentets belastning av spenningen som skal måles. 20 kOhm per V er en vanlig verdi for dreiespoler og tilsvarer en fullskala strøm på 50 uA. Verdien er oftest noe lavere for dreiejernsinstrumenter. Sannsynligvis ble det vanlig å benytte Ohm per V fordi instrumentets motstandsverdi ved det valgte måleområdet ble funnet ved meget enkel hoderegning og kunne sammenholdes med den målte kretsens følsomhet for belastninger. For eksempel vil et 20 kOhm per V instrument satt til 10 V fullskala utgjøre en motstandsverdi på 200 kOhm som belastning når det kobles inn i en krets.
For ikke å belaste måleobjektet har elektroniske forsterkere vært i bruk siden trioden ble oppfunnet og forsterkere kunne bygges. Slik ble begrepet rørvoltmeter synonymt med et ikke-belastende voltmeter i tiden før nesten alle voltmetere fikk forsterkerfunksjon med transistorteknikk, som i de digitale instrumentene.
Ved hjelp av elektroniske forsterkere kan også svært små spenninger måles.
Digitale instrumenter utnytter elektroniske forsterkere for avtasting av målespenningen og tilbyr oftest en fast verdi på 10 eller 11 MOhm belastning, uavhengig av det valgte måleområdet.
Vekselspenning[rediger | rediger kilde]

Dreiejerninstrumentet og det elektrodynamiske dreiespoleinstrumentet kan brukes for å måle vekselspenninger uten videre. Siden kraften på viseren er proporsjonal med kvadratet av målestrømmen, vil skalaen vise vekselspenningens effektivverdi. Siden målesystemene har relativt store induktanser, er frekvensområdet oppover noe begrenset.
Ved måling av vekselspenning med dreiespoleinstrument og digitale voltmetre dannes spenningen først om til en likespenning med en likeretter, og denne indikeres av et likespenningsinstrument.
Måling av vekselspenning ved hjelp av likeretting byr på en viktig prinsipiell utfordring: Med en vekselspennings verdi menes effektivverdien (eng: RMS-verdien) hvis ikke annet er sagt. Effektivverdien av en vekselspenning er per definisjon en likespenningsverdi som ville tilført en resistans den samme energimengden som den aktuelle vekselspenningen, uansett hvilken kurveform denne vekselspenningen måtte ha. I og med at det er denne likespenningsverdien som anvendes i de fleste beregninger, er det denne vi ønsker å kjenne til.
Utfordringen ligger i at både dreiespoleinstrumentet og de vanlige digitale instrumentene reagerer på (eller følger) gjennomsnittsverdien av den likerettede vekselspenningen, og at denne og effektivverdien nesten alltid vil ha forskjellige verdier. Eksempelvis for et sinussignal med 1 V amplitude (maksimalverdi) er effektivverdien mens den likerettede gjennomsnittsverdien er . For firkantsignaler er effektivverdien lik gjennomsnittsverdien.
Et sannferdig instrument ville altså vise 0.6366 V på skalaen for sinusspenning og 1 V for firkant.
Effektivverdien på 0,7071 V er ikke til stede i målekjeden. Den praktiske løsningen på dette dilemmaet ble å forfalske skalaen til instrumentet. For denne forfalskningen ble det lagt til grunn at det meste av vekselspenning som måles i praksis, har sinusform. Der det skulle stått 0.6366 på skalaen ble det skrevet 0.7071 i stedet for. Det er 0.7071/0.6366 = 1.111 ganger (11 %) for mye. Denne omkalibreringen virker egentlig utmerket, men naturligvis kun for sinussignaler. Signaler med andre kurveformer gir feilaktig avlesning. Bildet "Sann RMS" viser et eksempel utført med et firkantsignal. For firkantsignaler er amplitudeverdien lik effektivverdien, som igjen er lik (den likerettede) gjennomsnittsverdien, er her 1.0 V.
Hvor forskjellig signalet er fra en sinusform, angis av den såkalte crestfaktoren (spisshetsfaktoren kunne den kalles på norsk), som er definert som forholdet mellom maksimalverdien og effektivverdien. For sinussignaler er crestfaktoren altså, og for firkantsignaler er den lik 1.0.
For å måle den virkelige RMS- eller effektivverdien må målesignalet gå gjennom den prosessen som skjuler seg bak bokstavene RMS: Root of Mean of Squares: S, Square er kvadrering (resultatet er alltid positvt), M, Mean er midling av kvadratverdiene og R, Root er kvadratrottrekking av denne middelverdien. Dette kan gjøres både analogt og digitalt, men det er noe komplisert, og dermed kostbart. Instrumenter som er i stand til å gjennomføre slike målinger, er gjerne merket med "True RMS" (= "Sann RMS"). Den øvre grensefrekvensen som instrumentet kan behandle er ofte begrenset.
En alternativ måte å måle RMS-verdier på er å måle hvilken effekt signalet, eventuelt målrettet passende redusert eller forsterket, gir til en motstand i form av varme. For å oppnå presisjon brukes en målebro med to fysisk sett helt like motstander. Disse motstandene er svært små i størrelse. Den ene motstanden tilføres signalet og varmes opp på grunn av det. Den andre motstanden får tilført en likespenning fra en DC-forsterker som sørger for at temperaturene i de to motstandene blir nøyaktig like store. Dette gjøres automatisk ved hjelp av tilbakekobling. Den aktuelle DC-verdien vises som måleverdi. Ettersom frekvensen ikke spiller noen større rolle for varmedannelsen, kan denne målemetoden noenlunde enkelt benyttes for RMS-måling ved høye frekvenser. Instrumentet i bildet "Sann RMS" (klassiske Fluke 8920A) er av denne typen.
Skalaen på et dreiespoleinstrument uten forsterkerelektronikk er ikke linjær ved det laveste spenningsområdet, og særlig i den nedre delen av måleområdet. Dette kommer av at signalet må likerettes, og diodene som gjør dette er ikke linjære. Skalaen er gjort ikke-linjær for da å gi korrekt avlesning (for sinussignaler) likevel.
Spenninger som endrer seg[rediger | rediger kilde]
Dreiespoleinstrumentet er lettere å lese eller forstå enn digitalinstrumenter når spenningen stadig endrer verdi. Noen digitalinstrumenter har en slags viser, en såkalt "bargraph" (rettlinjet viser) for å rette på dette. Hvis spenningsendringer skjer hurtig, kan viseren til et dreiespoleinstrument eller bargraphen likevel ikke henge med. En er da henvist til et oscilloskop for å visualisere spenningens forløp over tid.
Analog-til-digital-omvandler[rediger | rediger kilde]
En analog-til-digital-omvandler (ADC) med spenningsinngang er også et voltmeter. Måleresultatet presenteres som en digital tallverdi som et signal på utgangen. Verdien kan plukkes opp av en mikroprosessor og lagres i et minne. Å finne en måleverdi kalles å ta et sample (en punktprøve) av inngangsspenningen. Oftest tas målinger fortløpende med en jevn frekvens som kalles sampleraten. De lagrete tallene beskriver spenningens tidsforløp. En ADC-krets får oftest tilført en nøyaktig, kjent, fast likespenning utenfra, fra en såkalt spenningsreferanse. Denne brukes til å sammenligne inngangsspenningen med.
Musikken fra CD-plater stammer eksempelvis fra slike samplete tall. Der er hvert sample representert med 16 bits, og det tas 44100 sampler per sekund for hver kanal når musikken digitaliseres. Like hurtig går det andre veien, når CD-platens tall omformes til varierende spenninger i en DAC, en digital-til-analog-omformer, som så gir den varierende spenningen til en forsterker og til høyttalerne. Et annet eksempel for bruk av en ADC er det digitale voltmeteret som er nevnt over. Utgangstallene presenteres på skjermen i klartekst, som regel uten å lagres. Denne ADC-en tar bare noen få sampler per sekund. Noen instrumenter lagrer maksimums- og minimumsverdier.
Det som i hovedsak bestemmer prisen på et voltmeter, er som regel dets presisjon, antall sifre som er pålitelige. Voltmetre med 3 1/2 og 4 1/2 sifre kan kalles vanlige, mens de som har 6 1/2 sifre er ganske dyre, og med 8 1/2 sifre er de nesten ubetalelige. Det halve sifferet i betegnelsen kommer av at det første sifferet er mindre enn 10 i verdi, oftest maksimalt 2 eller 4, og variasjon fra 0 til 4 utgjør ikke et helt siffers spennvidde.



