Ohms lov

Ohms lov sier at strømmen gjennom en metallisk leder med konstant temperatur er proporsjonal med den elektriske potensialforskjellen (spenningen) over den. Matematisk uttrykkes dette slik:
der I er strømmen gjennom lederen (i ampere), U er potensialdifferansen målt over lederen (i volt), og R er motstanden (eller resistansen) målt (i ohm). Figuren til høyre viser symbolene for en enkel elektrisk krets med en motstand og parametrene som inngår.
Loven er oppkalt etter den tyske fysikeren Georg Ohm. Ohm gjorde i en avhandling publisert i 1827 rede for målinger for påtrykt spenning og strøm gjennom enkle elektriske kretser som inneholder ulike ledere. Ohm oppdaget at spenningen over en metallisk leder ved konstant temperatur er proporsjonal med strømmen gjennom den. Det vil si at om spenningen dobles, dobles også strømmen. Han presenterte en litt mer komplisert ligning enn den ovenfor for å forklare resultatet av sine eksperimentelle studier.
Kretselementet motstand som brukes mye i elektriske og elektroniske kretser, også kalt en resistor, er et element laget for å ha en konstant R for alle tillatte påtrykte spenninger. Ohms lov er gyldig når R er konstant for konstant temperatur, uansett størrelsen av spenningen. Hvis R i et element i en krets derimot varierer, for eksempel med strømmen, kalles det ikke-Ohmsk motstand eller ikke-lineært kretselement. Et eksempel på dette er halvledere, lysbuer og ledende væsker, som endrer motstandsverdien sin i forhold til påtrykt spenning. Formelen definerer uansett en motstandsverdi i alle tilfeller, også når motstanden ikke har konstant verdi ved variasjon av strøm og spenning, altså ikke følger Ohms lov.
I fysikken er begrepet Ohms lov også brukt for å referere til ulike generaliseringer av loven opprinnelig formulert av Ohm. Det enkleste eksempelet på dette er:
hvor J er strømtetthet på et gitt sted i et resistivt materiale, E er det elektriske feltet på dette stedet og σ (Sigma) er et materialavhengig parameter kalt konduktivitet. Uthevede symboler betyr at vektorer er innført fordi både størrelse og retning har betydning.
Historie
[rediger | rediger kilde]

Georg Ohms undersøkelser
[rediger | rediger kilde]I 1781 eksperimenterte Henry Cavendish med Leidnerflaskeer og glassrør av ulik diametere og lengde, fylt med saltløsning. Han målte strøm ved å merke seg hvor sterkt sjokk han følte da han berørte terminalen til disse. Cavendish skrev at «hastighet» (strøm) varierte direkte som «grad av elektrifisering» (spenning). Han gjorde ikke sine resultater kjent til andre forskere på den tiden,[1] og hans resultater var ukjent inntil James Clerk Maxwell publisert dem i 1879.[2]
Ohm gjorde sitt arbeid vedrørende elektrisk motstand i årene 1825 og 1826, og publiserte sine resultater 1. mai 1827 som boken Die galvanische Kette, mathematisch bearbeitet («Den galvanisk krets undersøkt matematisk»).[3] Her var han inspirert av Joseph Fouriers arbeid med varmeledning i den teoretiske delen av arbeidet. For eksperimentene bruket han opprinnelig Voltasøyler, men senere gikk kan over til termoelementer som utgjorde en mer stabil spenningskilde. (På grunn av stabil indre motstand og konstant spenning). Han brukte et galvanometer for å måle strømmen, og visste at spenningen mellom klemmene til termoelementet var proporsjonal med temperaturen i elementet. Deretter tilkoblet han testledninger av varierende lengde, diameter og materiale for å få en sluttet krets for å utføre målinger på. Han fant at måledataene kunne modelleres gjennom ligningen:
hvor x var avlesningen fra galvanometret, l er lengden av testlederen, a er spenningen og b er en konstant for hele oppsettet. Ut fra dette fant Ohm sin lov om forholdsmessighet mellom spenning og strøm, og publiserte sine resultater. Opprinnelig hadde ikke Ohm med motstand i sin formulering av sammenhengen mellom strøm og spenning. Begrepet motstand er innført senere.[4]
Ohms lov var sannsynligvis den viktigste av de tidlige kvantitative fysiske beskrivelser av elektrisitet. En anser loven nesten som opplagt i dag. Når Ohm først publiserte sitt arbeid var ikke dette tilfelle: Kritikere reagerte på hans behandling av temaet med fiendtlighet. De kalte kalte verket "en vev av nakne innfall"[5] Den tyske utdanningsministeren proklamerte at: – En professor som forkynte slike vranglære var uverdig å undervise vitenskap.[6] Den rådende vitenskapsfilosofi i Tyskland på den tiden hevdet at forsøk ikke trenger å bli utført for å utvikle en forståelse av naturen, dette fordi naturen er så godt organisert at vitenskapelige sannheter kan utledes gjennom resonnementer alene.[7] Også Ohms bror Martin, som var matematiker, var i opposisjon til det tyske utdanningssystemet. Dette hindret aksept av Ohms arbeid, dermed ble ikke hans oppdagelser allment akseptert før i 1840-årene. Heldigvis fikk Ohm anerkjennelse for sine bidrag til vitenskapen i god tid før han døde.
I 1850-årene ble Ohms lov viden kjent og ble ansett som bevist. Alternative oppfatninger for eksempel Barlows lov, ble diskreditert i forbindelse med konstruksjon av telegrafsystemer, som omtalt av Samuel Morse i 1855.[8]
Moderne forskning
[rediger | rediger kilde]På 1920-tallet ble det oppdaget at strømmen gjennom en virkelig motstand faktisk har stokastiske svingninger som avhenger av ledertemperaturen, selv når spenning og motstand er nøyaktig konstant. Disse svingningene er nå kjent som Johnson-Nyquist støy og skyldes den diskrete naturen til elektriske ladninger. Denne termiske effekten innebærer at målinger av strøm og spenning som foretas over tilstrekkelige korte perioder vil gi prosentvise variasjoner av V/I-forholdet. Det vil si at verdien av R er påvirket av tiden der målingen av motstanden for en leder gjøres. Ohms lov forblir imidlertid riktig for den gjennomsnittlige strømmen for vanlige motstandsmaterialer.
Ohms lov får med innføring av begrepet impedans, som har med frekvensavhengige fenomener i vekselstrømskretser å gjøre, også gyldighet i kretsanalyser av denne typen. Moderne utvikling i elektromagnetisk teori og kretsteori gjør ikke Ohms lov ugyldig, forutsatt at loven blir anvendt innenfor sitt gyldighetsområde.
Senest for noen år siden ble det påvist at Ohms lov også gjelder på atomært nivå. Selv for ledere med bare noen få atomer bredde og høyde som fører elektrisitet stemmer sammenhengen.
Anvendelse av Ohms lov
[rediger | rediger kilde]Kretsanalyse
[rediger | rediger kilde]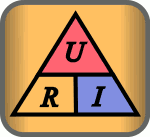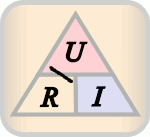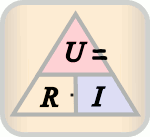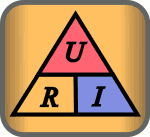
Ohms lov sier at elektrisk strøm gjennom en leder mellom to punkter er direkte proporsjonal med den elektriske potensialforskjellen (spenningen) mellom de to punktene. Som to punkter kan hvilke som helst steder i kretsen velges. For eksempel kan det være naturlig å velge de to terminalene til et kretselement (motstand) slik som vist i figuren helt øverst.
Ved å innføre en proporsjonalitetskonstant kalt resistans fås den kjente matematiske ligning som beskriver forholdet mellom strøm og spenning:[9]
På denne formen fastslår Ohms lov at R i denne sammenhengen er konstant, dessuten uavhengig av strømmen eller spenningen. For en hver elektrisk krets kan ligningen brukes, men det er kun der det er direkte proporsjonalitet mellom U og I at Ohms lov er gyldig.[9] Lenger ned blir det nevnt tilfeller der U og I ikke er proporsjonale.
I kretsanalyse er de tre mulige formene av Ohms lov brukt om hverandre som likeverdige uttrykk:
Måleenheten for spenning er Volt (V) og er et uttrykk for elektrisk potensialforskjell i en elektrisk krets. Potensialforskjellen gjelder mellom to punkter i et elektrisk felt. Strømstyrke eller ofte bare kalt «strøm» måles i ampere (A) og er et uttrykk for nettoflyten av ladninger gjennom et ledertverrsnitt per tidsenhet. Om det går 1 A gjennom en leder vil det si at en ladningsmengde på 1 Coulomb (C) passerer et ledertverrsnitt per sekund. Motstanden eller resistansen måles i ohm (Ω) og er definert ut fra enhetene Volt og ampere slik: Om det i en leder påtrykkes en spenning på 1 V og den fører en strømstyrke på 1 A, er motstanden 1 Ω. Altså brukes Ohms lov for å definere motstand. Motstanden i en leder er avhengig av materialets resistivitet som er en materialegenskap, samt av tverrsnittet (arealet) og lengde av lederen.
De tre formene av ligningen kan representeres av en trekant, hvor U (spenning) er plassert i den øvre delen, I (strømmen) er plassert i venstre nedre delen, og R (motstanden) er plassert i den høyre nedre del. Se figur over til høyre. Linjen som skiller den venstre og høyre delene indikerer multiplikasjon og delelinjen mellom de øvre og nedre delene angir divisjon (brøktegn). Denne fremstillingen kan brukes som en huskeregel.
Hydraulisk analogi
[rediger | rediger kilde]En hydraulisk analogi er ofte brukt for å beskrive Ohms lov. Væsketrykket er analogt med spenningen, dette på grunn av at potensialforskjellen (trykkforskjellen, målt i for eksempel Pa) mellom to punkter langs et (horisontalt) rør som får væsken til å strømme. Strømningshastighet (målt i liter per sekund) er analogt med strømstyrken, som er Coulomb per sekund. Rørfriksjonen som gir trykkfall i røret er analogt med ledermotstanden. Videre kan en innsnevring av røret være analog med en motstand (et kretselement). En kan observere at væskemengden (liter per sekund) gjennom røret, eller gjennom en innsnevring, er proporsjonal med forskjellen i væsketrykk over denne. Analogt med at strømningshastigheten av elektrisk ladninger, det vil si strømstyrken, gjennom en elektrisk motstand er proporsjonal med forskjellen i spenning som måles over motstanden.
Sluttet krets
[rediger | rediger kilde]En forutsetning for at det skal gå en strøm og at Ohms lov kan anvendes, er at en har en sluttet krets. Dette kan synes innlysende, men en fysisk forklaring kan være interessant. Om en kan sette opp et elektrisk felt i en isolert leder som ikke er del av en krets, vil det gå en strøm som er bestem av motstanden og styrken på feltet. Meget snart vil positive og negative ladninger i lederen orientere seg i forhold til feltet. Dermed vil det være positiv polaritet i den ene enden av lederen og negativ i den andre. Ladningene selv danner et elektrisk felt som vil være motsatt rettet av det opprinnelige feltet. Etter bare noen få brøkdeler av et sekund vil disse to elektriske feltene være like store og motsatt rettet, dermed vil det resulterende elektriske feltet være lik null. Dermed vil også netto forflytting av ladninger, altså strømstyrken, like raskt bli lik null.[10]
Bare i en sluttet krets med en spenningskilde vil det være strømflyt. En stasjonær situasjon vil da oppstå der den samme ladningsflyten, altså strømstyrken, gjennom alle tverrsnitt av kretsen er den samme. For lommelykter, og lignende utstyr med batterier som drivende spenningskilde vil strømmen ha samme retning, i tillegg til å være jevn. Dette i motsetning til i systemer med vekselstrøm hvor strømretningen og spenningen skifter retning i takt med frekvensen.
Elektromotorisk spenning
[rediger | rediger kilde]Utdypende artikkel: Elektromotorisk spenning
Over ble det nevnt at Ohms lov for en elektrisk krets har en hydraulisk analogi. På samme måte som det i en hydraulisk krets er nødvendig med en pumpe for å få en vannstrøm til å gå fra et lavere til et høyre nivå over bakken (potensial), er det nødvendig med en drivende kilde i en elektrisk krets. Denne kilden kalles for en elektromotorisk spenning, forkortet EMS, og ofte gitt symbolet . Tidligere ble denne størrelsen kalt elektromotorisk kraft (EMK). Enheten for EMS er volt, og en av flere definisjoner av volt er: 1 V = 1 J/C. Altså at 1 volt utfører et arbeid tilsvarende 1 Joule når en ladning på 1 Columb blir flyttet. Denne definisjonen passer godt for å illustrere at det arbeidet som utføres i en elektrisk krets, er det den elektromotorisk spenning som står bak. Typiske eksempler på spenningskilder er batterier, solceller, generatorer, brenselceller, Van de Graaff generator og flere andre. Alle disse har en indre EMS som blir skapt ved en omvandling fra en energikilde til elektrisk energi som kreves for å drive rundt strømmen i kretsen. Kildene kan være for eksempel kjemisk energi, sollys eller rotasjonsenergi (kinetisk energi). Den ideelle kilde til EMS (spenningskilde) er definert ved å gi en konstant spenning ut på terminalene, uavhengig av strømmen (belastningen).
Det som skaper EMS kan være høyst forskjellig etter hva slags kilde en har. I et batteri eller brenselcelle er det snakk om diffusjonsprosesser og varierende elektrolytiske potensialer som skapes av kjemiske reaksjoner. I en generator er det snakk om elektromagnetisk induksjon på grunn av et varierende magnetisk felt som påvirker ladninger (elektroner). Det er et elektrisk felt som danner potensialforskjellen som altså kalles EMS, og dette feltet kan dannes på vidt forskjellige måter.[10]

Om en ser på situasjonen med et batteri vil dette ha en EMS, noe som gir en spenning ut på dets terminaler. Kaller en spenningen ved positiv terminal Ua og ved negativ terminal Ub, er spenningen mellom de to terminalene Uab = Ua - Ub. Uten noen elektrisk krets tilkoblet batteriet er .[10]
Om en tilknytter en elektrisk leder til de to terminalene vil potensialforskjellen mellom disse sette opp et elektrisk felt i lederen. Det er dette elektriske feltet som får ladningene til å flyte ut av batteriet, fra terminal a, gjennom kretsen som lederen danner og tilbake til terminal b. Inne i selve batteriet flytter ladningene seg derimot fra b til a, altså går ladningene i en sluttet krets. Motstanden i lederen virker mot ladningstransporten, og Ohms lov beskriver spenningen slik: Uab = IR. Ved å kombinere sammenhengen for EMS og spenningsfall i ledningen som tilknyttes batteriet får en at:
Her er det som gir ladningsbærerne i kretsen en potensialøkning, mens IR representerer et potensialfall. Potensialfall i en elektrisk krets er vanligvis kalt spenningsfall. Imidlertid gjelder ligningen over kun for en idel spenningskilde, altså at den er uten motstand. I en virkelig spenningskilde som et batteri vil det være en indre motstand, som en kan kalle r. Om en antar at denne motstanden oppfører seg i henhold til Ohms lov, altså at den er konstant og uavhengig av strømmen, kan spenningsfallet inne i lederen uttrykkes som Ir. Dermed vil ikke spenningen ved terminalene Uab, være lik , men isteden kunne uttrykkes slik:
Med andre ord vil et lommelyktbatteri med en spenning på 1,5 V egentlig bare gi ut denne spenningen når det er ubelastet. Spenningen over batteriets terminaler vil falle proporsjonalt med strømmen det leverer til den ytre kretsen. Dette forholdet har en også i en generator, en solcelle eller en annen spenningskilde.
Her bemerkes det at i kretsanalyse brukes forskjellige fortegn for spenningen. Om det som over er snakk om en spenningskilde brukes som regel positivt fortegn, mens det for spenning over en motstand brukes negativt fortegn. Altså positivt fortegn for potensialøkning og negativt for potensialfall. I en sluttet elektrisk krets der denne fortegnkonvensjonen brukes vil summen av alle spenningene rundt kretsen være lik null. Dette kalles Kirchhoffs strømlov og er oppkalt etter den tyske fysikeren Gustav Kirchhoff.
Resistive kretser
[rediger | rediger kilde]
En motstand (resistor) er et kretselement som motvirker passering av elektrisk ladning i henhold til Ohms lov, og lages for å ha en spesifikk konstant motstandsverdi R. Motstander som brukes i elektroniske kretser har typiske verdier fra 0,01 til 107Ω.[11]
I et skjematisk diagram er motstanden vist som en sikk-sakk-symbol eller som et rektangel. Motstander som er i seriekobling eller i parallellkopling kan grupperes sammen i en enkelt «ekvivalent motstand» for å anvende Ohms lov. Et element (motstand eller leder) som oppfører seg i samsvar med Ohms lov over en viss driftsområdet (strømstyrke- eller svingningsintervall) er referert til som en ohmske motstand (eller en lineær motstand). En enkelt verdi for motstanden vil være tilstrekkelig til beskrive virkemåten til den innenfor dette intervallet.
Ohms lov gjelder for kretser som inneholder bare motstandselementer (ikke kapasistanser eller induktanser) for alle formene av drivende spenning eller strøm. Dette gjelder uavhengig av om den drivende spenning eller strøm er konstant (likestrøm), eller tidsvarierende som vekselstrøm. Ved en hvilken som helst tidsøyeblikk er Ohms lov gyldig for slike kretser. For kretser med vekselstrøm blir det nødvendig å innføre flere begreper for at Ohms lov skal kunne anvendes.
Reaktive kretser med vekselstrøm
[rediger | rediger kilde]Utdypende artikkel: Vekselstrøm

En elektrisk spole er et elektrisk kretselement der en leder er viklet opp, omtrent som sytråd på en trådsnelle. Spolen har to terminaler som kan tilknyttes en elektrisk krets. Denne vil kun ha resistivitet om den leder likestrøm, men med vekselspenning kommer det en egen motstand i tillegg som kalles induktiv reaktans. En kondensator er et annet kretselement som består av to tynne deler av metallfolie med et isolasjonsmedium imellom. Hver av metallfoliene er tilknyttet en terminal som kan tilkobles en ytre elektrisk krets. Om en tilknytter en kondensator til en likestrømkrets virker den som et brudd i kretsen, derimot om den tilknyttes vekselspenning går det elektrisitet gjennom den. Kondensatoren har i en slik krets en motstand som også kalles reaktans (kapasitiv reaktans).
Det er innført følgende matematiske begrep for en spole:
og for en kondensator,
- .
der j er den imaginære enheten , mens vinkelfrekvensen der igjen f er frekvensen (Hz) i vekselstrømsystemet. L er induktansen for spollen og C er kapasitansen for kondensatoren. Disse størrelsene er bestemt av geometriske forhold og materialene som er bruk. Videre har en innført begrepet impedans som er sammensatt av den ohmske-motstanden i kretsen og reaktansen. Denne defineres som summen av ohmske og reaktive motstander
Impedansen er derfor i alminnelighet en kompleks størrelse. En kan nå skrive Ohms lov på denne generelle formen:
hvor U og I er de komplekse fasevektorene for henholdsvis spenning og strøm og Z er den komplekse impedansen. Med vekselstrøm tar altså denne plassen til R i Ohms lov. Når Z er kompleks, altså består av både R og X, er det bare den reelle delen som avgir varme. Definisjonene over gjelder bare for sinusformede strømmer og spenninger.
Eksempler på bruk av Ohms lov
[rediger | rediger kilde]Si at startmotoren for å dra i gang motoren i en bil bruker en strøm på 200 A[12]. Batteriet i en bil har typisk en spenning på 12 V. Hva er da motstanden gjennom ledningen fra batteriet, gjennom startmotoren og tilbake til batteriet?
Ved å bruke den formen av Ohms lov som gir motstanden finner en at:
Si at elektrisk ledning har en impedans på ZL = 1 + j4 Ω og er tilknyttet en elektrisk apparat (last) med motstand ZLast = 39 + j26 Ω. En spenningskilde holder konstant 250 V i begynnelse av ledningen. Hva er spenningen ved apparatet?
Først må en finne strømmen. Kretsen er i serie med spenningskilden, dermed finner en strømmen ved å benytte Ohms lov direkte med hensyn på strømmen:
Her er strømmen vist både som komplekse størrelser både med sine kartesiske og polare verdier. Spenningen over lasten finner en ved å bruke Ohms lov direkte med hensyn på spenningen:
I praksis er en ikke så interessert i fasevektoren som sier at spenningen ble fasevforskjøvet med -3,18º. Derfor holder det å si at spenningen ved apparatet er 234,36 V. Eksemplet kan være for en transformator (nettstasjon) og inn til et hus der alle elektriske apparater er ekvivalert med én impedans (last).
Fenomener ved elektrisk ledning
[rediger | rediger kilde]Gyldighetsområde
[rediger | rediger kilde]Ohms lov er en empirisk lov, det vil si en generalisering ut fra mange eksperimenter som har vist at strømmen er omtrent proporsjonal med elektrisk spenning for de fleste materialer. Loven er mindre generell enn Maxwells ligninger og er ikke alltid gyldig. I et hvert materiale vil elektrisk sammenbrudd inntreffe om det utsettes for et sterk nok elektrisk spenning, og noen materialer som anvendes i elektroteknikk er «ikke-ohmske» ved lave spenninger.[13][14]
Spesielt for metaller gjelder Ohms lov nesten helt lineært, men vil endres om temperaturen til lederen ikke er konstant. For halvledere gjelder Ohms lov dårlig, det samme gjelder ved strøm gjennom gasser (plasma eller lysbue) og væsker (ioneoppløsninger).
Gyldigheten for Ohms lov har blitt studert på mange forskjellige skalaer. På begynnelsen av 1900-tallet ble det antatt at Ohms lov ville gi dårlige resultater på et atomært nivå, men forsøk som har vært utført har ikke bekreftet denne antagelsen. I 2012 ble det demonstrert at Ohms lov er gyldig for ledere av silisium med et tverrsitt av fire atomer i bredden og ett atom i høyden.[15]
Ohms lov fra at et atomært perspektiv
[rediger | rediger kilde]

Avhengighet mellom strømtettheten og det påtrykte elektriske feltet er i det vesentlige av kvantemekanisk natur. En kvalitativ modell for Ohms lov er Drudes modell. Denne er basert på klassisk mekanikk og utviklet av Paul Drude i 1900.[16][17]
Drude-modellen ser på elektronene (eller andre ladningsbærere) som baller som spretter rundt blant ionene som utgjør selve strukturen i materialet. Elektroner vil bli akselerert i den motsatte retningen av det elektriske feltet som er årsaken til strømflyten. Frie elektroner i et metall vil ha en hastighet på 106 m/s[18] der de beveger seg mellom atomene. Ved hver kollisjon blir elektronene avbøyd i en tilfeldig retning med en hastighet som er mye større enn den hastigheten som ble oppnådd på grunn av det elektriske feltet. Nettoresultatet er at elektronene tar en sikksakk-bane på grunn av kollisjoner, men får allikevel en netto drift i en retning motsatt av det elektriske feltet. Dette kalles elektonenes driftshastighet, og er typisk i størrelsesorden av 10-4 m/s[18].
Denne driftshastigheten bestemmer elektrisk strømtetthet og dens forhold til E er uavhengig av kollisjonene. Drude beregnet gjennomsnittlig driftshastighet som v = -eEτ/m der -e er elektronets ladning med masse m og τ er den gjennomsnittlige tiden mellom kollisjonene. Siden strømtettheten er proporsjonal med driftshastigheten, blir strømtettheten proporsjonal med det påtrykte elektriske feltet, som igjen er Ohms lov.
Når det skjer en forflytning av ladninger i en elektrisk leder på grunn av et elektrisk felt, tilføres kinetisk energi til materialet. Dette fører til hyppigere kollisjoner mellom ioner, som igjen fører til at ionene blir ført opp til høyere energinivåer. Som resultat tilføres ionene vibrasjon i krystallstrukturene som de er en del av. I glødetråder i varmeovner og lyspærer er dette en ønskede effekt, men i en kraftledning er dette en ulempe fordi det fører til tapt energi.[18]
Til nå er det nevnt elektroner som ladningsbærere, men det er nødvendigvis bare elektroder som er ladningsbærere for en elektrisk strøm. I metaller er ladningbærerne alltid elektroner, men i ionisert gass (plasma) eller i en ioneoppløsning kan ladningbærerne være både elektroner og positivt ladede ioner. I halvledere som germanium og silisium skjer ladningbæringen delvis med elektroner og såkalte hull. Hull er plasser i materialets atomstruktur som er tomme på grunn av såkalt doping av metallet.[19]
For en elektrisk leder som blir utsatt for et elektrisk felt vil positive ladningsbærere gå i samme retning. I praksis vil det si at ladninger beveger seg fra positivt til negativt potensial. Strømmen I er definert til å gå fra positiv til negativ pol. En kaller dette for den konvensjonelle strømretning. Imidlertid vil ikke dette nødvendigvis alltid være tilfelle, og for elektroner som er ladningsbærere i metaller vil altså strømretningen være i motsatt retning av feltet. I praktisk analyse av elektriske kretser er imidlertid ikke dette av stor viktighet.[20]
Lineære tilnærminger
[rediger | rediger kilde]
Ohms lov er en av de grunnleggende ligningene som brukes i elektrisk kretsanalyse. Det gjelder både metalledere og kretskomponenter (motstander) som er spesielt laget for formålet. Begge er allestedsnærværende i elektroteknikken. Materialer og komponenter som følger Ohms lov betegnes som «ohmske»[21] eller lineære. Noe som betyr at de har den samme verdien for motstand (R = U/I) uavhengig av verdien av U eller I som påtrykkes. Dette gjelder uavhengig av om den påtrykte spenning eller strømmen er en likestrøm av enten positiv eller negativ polaritet, eller en vekselstrøm.
Et ohmsk motstandselement vil ha den samme verdi av motstanden som beregnes ut fra R = U/I, uavhengig av verdien av den påtrykte spenning U. Det vil si at forholdet U/I er konstant, og når strømmen blir plottet som en funksjon av spenningskurve fås en rett linje der R er stigningstallet.
Det er imidlertid en rekke komponenter i elektriske kretser som ikke følger Ohms lov. Det vil si at forholdet mellom strøm og spenning (elementets I-U-kurve) er ikke-lineær (eller ikke-ohmsk). Et eksempel er en diode (se illustrasjon til høyre). Som vist i figuren vil ikke strømmen øke lineært med påtrykt spenning for en diode. En kan bestemme en verdi av strømmen (I) for en gitt verdi av den påtrykte spenning (U) fra kurven, men ikke i henhold til Ohms lov. Videre vil strømmen bare øke betydelig hvis den påtrykte spenning er positiv, men for negativ spenning øker strømmen ubetydelig. Forholdet U/ I for punkter langs den lineær kurve kalles ofte statikk eller stigningen.[22][23]
En diode er et kretselement som bare skal lede strøm om spenningen over den har en bestemt polaritet (retning). Derfor har den en karakteristikk som vist i figuren. Et batteri som er vist i figuren helt til høyre har en karakteristikk mellom strøm og spenning som viser at det har indre motstand. Strømmen antar både negative og positive verdier fordi det kan lades opp (mota energi).
Andre versjoner av Ohms lov
[rediger | rediger kilde]Ohms lov i formene ovenfor er en svært nyttig ligning innen elektroteknikk fordi den beskriver hvordan spenning, strøm og motstand henger sammen på et "makroskopisk" nivå. Fysikere som studerer de elektriske egenskapene til materialer på mikroskopisk nivå bruker en nært beslektet og mer allmenn vektorligning. Denne blir ofte referert til som Ohms lov og har variabler som er nært knyttet til U , I og R, men der parametrene er funksjoner av posisjonen i lederen. Denne formen uttrykkes slik:[24]
hvor E er en vektor for det elektriske feltet med enheten volt per meter (som er analog med U i Ohms lov), J som er en vektor for strømtettheten som måles i ampere per arealenhet (analogt til I i Ohms lov), og ρ som er resistiviteten med enhet av ohm·meter (som er analogt med R i Ohms lov). Ligningen over er noen ganger skrevet[25] som J = σ E, der σ er ledningsevne som er den inverse verdien av ρ.

Den potensielle forskjellen mellom to punkter er definert som:[26]
der er et element som blir integrering over den elektriske feltvektoren E. Hvis det aktuelle feltet E er homogent og orientert langs lengden av lederen som vist i figuren til venstre, kan en definere spenningen U på vanlig måte for å være motsatt rettet i forhold til strømbanen. Med forutsettelsen om at spenningen U måles over hele lengden av lederen kan en unngå Δ-symbolet. Dermed kan vektorligningen ovenfor reduseres til en ligning med skalare verdier:
Siden E er homogen langs trådlengden, vil det for en leder som har homogen resistivitet ρ, også være en jevn strømtettheten J. Det vil si at strømmen er ensartet i en hvilken som helst tverrsnittsareal med størrelse a og orientert i retning av lederens lengde. Dermed kan en skrive:
Ved å erstatte de to ligningene over (for henholdsvis E og J) inn i den formelen som ble vist helt i begynnelsen av dette avsnitt fås:

Den elektrisk motstand av en homogen leder er gitt i form av resistivitet:
hvor l er lengden på lederen i meter, a er tverrsnittet (for en runde leder a = π r 2 der r er radius) i kvadratmeter, og ρ er resistiviteten i ohm·meter. Denne sammenhengen for motstand kjenner en igjen som det siste leddet i ligningen for spenning over. Dermed kan en sette inn R fra den overstående ligning i den foregående, dermed fås Ohms lov i den kjente formen:
Som altså gjelder for et homogent felt langs lengden av lederen.
En perfekt krystallgitter, med lav nok termisk bevegelse og ingen avvik fra periodisk struktur, vil ikke ha noen resistivitet,[27] men et virkelig metall har krystallografiske defekter, urenheter, flere isotoper, og termisk bevegelse av atomene. Dermed blir Drudes modell som ser på elektroner som baller som sprette mellom atomene aktuell. Altså at elektronbevegelsen resulterer i motstand.
De mer komplekse generelle former av Ohms lov er viktig for kondenserte fasers fysikk som studerer egenskaper av materialer, spesielt deres atomstruktur.
Effekten av temperatur
[rediger | rediger kilde]Resistans eller resistiviteten for et ledermateriale er som nevnt temperaturavhengig. Nesten for alle metalliske lederer øker motstanden med økt temperatur. Den økte temperaturen fører til hurtigere vibrasjon av ionene i metallet, noe som igjen øker sannsynligheten for at elektroner i bevegelse skal kollidere med dem. For et temperaturintervall fra null til 100 °C gjelder følgende sammenheng for resistivitetens ρ temperaturavhengighet:
der er resitiviteten ved referansetemperatur T0 (ofte ved 20 °C). Videre er T den aktuelle temperaturen og α er temperaturkoeffisienten for resistivitet. Som et eksempel kan nevnes at kobber og aluminium begge har en temperaturkoeffisient på 0,0039.[28]
På grunn av at strømgjennomgang er medfører oppvarming av lederen, i henhold til Joules lov, vil en leder selv bidra til høyere temperatur og dermed høyere motstand.
Se også
[rediger | rediger kilde]- Varmeledning
- Elektrisitet
- Elektronikk
- Noen ganger brukes «Ohms akustiske lov» om mekanisk impedans, «Ohms magnetiske lov» om magnetisk reluktans, og «Ohms varmeledningslov» om varmeledning.[29]
Referanser
[rediger | rediger kilde]- ^ «Electricity». Encyclopædia Britannica. 1911. Arkivert fra originalen 15. september 2008.
- ^ Sanford P. Bordeau (1982) Volts to Hertz...the Rise of Electricity. Burgess Publishing Company, Minneapolis, MN. pp.86–107, ISBN 0-8087-4908-0
- ^ G. S. Ohm (1827). Die GALVANISCHE Kette, Mathematisch bearbeitet. Berlin: T. H. Riemann.
- ^ Young og Freedman: University physics side 853.
- ^ Davies, B, "A web of naked fancies?", Physics Education 15 57–61, Institute of Physics, Issue 1, Jan 1980 [1]
- ^ Hart, IB, Makers of Science, London, Oxford University Press, 1923. p. 243. [2] Arkivert 8. mars 2008 hos Wayback Machine.
- ^ Herbert Schnädelbach, Philosophy in Germany 1831-1933, pages 78-79, Cambridge University Press, 1984 ISBN 0521296463.
- ^ Taliaferro Preston (1855). Shaffner's Telegraph Companion: Devoted to the Science and Art of the Morse Telegraph. Vol.2. Pudney & Russell.
- ^ a b Young og Freedman: University physics side 853.
- ^ a b c Young og Freedman: University physics side 857.
- ^ Young og Freedman: University physics side 854.
- ^ Young og Freedman: University physics side 848.
- ^ Purcell, Edward M. (1985), Electricity and magnetism, Berkeley Physics Course, 2 (2nd utgave), McGraw-Hill, s. 129,
- ^ Griffiths, David J. (1999), Introduction to electrodynamics (3rd utgave), Prentice Hall, s. 289,
- ^ Weber, B.; Mahapatra, S.; Ryu, H.; Lee, S.; Fuhrer, A.; Reusch, T. C. G.; Thompson, D. L.; Lee, W. C. T.; Klimeck, G.; Hollenberg, L. C. L.; Simmons, M. Y. (2012). «Ohm's Law Survives to the Atomic Scale». Science. 335 (6064): 64–67. doi:10.1126/science.1214319.
- ^ Drude, Paul (1900). «Zur Elektronentheorie der metalle». Annalen der Physik. 306 (3): 566. Bibcode:1900AnP...306..566D. doi:10.1002/andp.19003060312.[død lenke]
- ^ Drude, Paul (1900). «Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte». Annalen der Physik. 308 (11): 369. Bibcode:1900AnP...308..369D. doi:10.1002/andp.19003081102.[død lenke]
- ^ a b c Young og Freedman: University physics side 847.
- ^ Young og Freedman: University physics side 847-848.
- ^ Young og Freedman: University physics side 848.
- ^ Hughes, E, Electrical Technology, pp10, Longmans, 1969.
- ^ Forbes T. Brown (2006). Engineering System Dynamics. CRC Press. s. 43. ISBN 978-0-8493-9648-9.
- ^ Kenneth L. Kaiser (2004). Electromagnetic Compatibility Handbook. CRC Press. s. 13–52. ISBN 978-0-8493-2087-3.
- ^ Lerner, Lawrence S. (1977). Physics for scientists and engineers. Jones & Bartlett. s. 736. ISBN 978-0-7637-0460-5.
- ^ Seymour J, Physical Electronics, Pitman, 1972, pp 53–54
- ^ Lerner L, Physics for scientists and engineers, Jones & Bartlett, 1997
- ^ Seymour J, Fysisk Electronics , s 48-49, Pitman, 1972
- ^ Young og Freedman: University physics side 852.
- ^ Glossar - Ohm "Darauf beruht die Elektrotechnik. Weniger bekannt sind das ohmsche Gesetz der Akustik (mech. Impedanz), des Magnetismus (magnet. Widerstand) und der Wärmeleitung (Thermostatik)."
Litteratur
[rediger | rediger kilde]- Hugo D. Young og Roger A. Freedman (2008). University Physics (engelsk) (XII utg.). Addison Wesley. ISBN 978-0-321-50130-1.
Eksterne lenker
[rediger | rediger kilde]- (en) Ohm's law – kategori av bilder, video eller lyd på Commons
- John C. Shedd and Mayo D. Hershey,"The History of Ohm's Law", Popular Science, December 1913, pages 599-614, Bonnier Corporation ISSN 0161-7370, gives the history of Ohm's investigations, prior work, Ohm's false equation in the first paper, illustration of Ohm's experimental apparatus.
- Morton L. Schagrin, "Resistance to Ohm's Law", American Journal of Physics, July 1963, Volume 31, Issue 7, pp. 536–47. Explores the conceptual change underlying Ohm's experimental work.
- Kenneth L. Caneva, "Ohm, Georg Simon." Complete Dictionary of Scientific Biography. 2008
- C. Blondel and B. Wolff, CNRS, Historien bak Ohms lov, på fransk.





























![{\displaystyle \rho =\rho _{0}[1+\alpha (T-T_{0})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f5b9313a5f6bbc146f9f7b00eb91e79457aa799)
