Projektivt plan

Projektivt plan er en flate bestående av punkter og linjer som har egenskaper gitt ved projektiv geometri. Denne er mer fundamental enn euklidsk geometri ved at parallelle linjer ikke lenger finnes og heller ikke entydige sirkler. Den får dermed en mye løsere og generell struktur. Alle linjer skjærer hverandre i et punkt. Vinkler og lengder av linjestykker er ikke lenger meningsfulle konsept. I stedet vil det primære begrepet i det projektive planet være skjæringspunkt mellom linjer.
Det projektive planet er ikke plant i vanlig forstand, men må forstås som en abstrakt, matematisk flate. Hvis man prøver å forestille seg den i vårt vanlige, tredimensjonale rom, ville denne flaten se ut til å gå gjennom seg selv. Dette ville unngås hvis den befant seg i et rom med ekstra dimensjoner.
Allerede i renessansen ble den første innsikt i egenskapene til det projektive planet etablert i forbindelse med fremstillingen av perspektiv i bilder. To bilder malt på forskjellige ståsteder, vil i alminnelighet se forskjellige ut. Et rektangel vil for eksempel bli avbildet som en skjev firkant, mens en sirkel vil bli seende ut som en ellipse eller et annet kjeglesnitt. Men ved slike perspektiviske fremstillinger vil en linje alltid avbildes som en linje og dens skjæringspunkt med andre linjer vil kun flyttes, ikke forsvinne. Parallelle linjer i motivet vil se ut til å skjære hverandre i et forsvinningspunkt i bildet. Dette ligger på horisonten som er avbildningen av punktene som ligger uendelig langt borte.
Den fulle forståelse av det projektive planet har hatt betydning for utviklingen av ikke-euklidsk geometri. I dag er det av stor praktisk betydning i forbindelse med bildebehandling og datagrafikk. Vanligvis betegnes det projektive planet som P2 eller som RP2 for å understreke at det er beskrevet med koordinater som er reelle tall. Hvis man i stedet hadde benyttet komplekse tall, vil det betegnes som CP2. Dette komplekse, projektive planet er matematisk interessant og blir også studert med tanke på anvendelser innen teoretisk fysikk.
Postulater[rediger | rediger kilde]
På samme måte som euklidsk geometri ble formulert ved en rekke definisjoner og aksiomer samlet sammen i Euklids verk Elementer, kan også egenskapene til det projektive planet defineres. Man antar som gitt at planet inneholder punkter og linjer som kan være insidente, det vil si at et punkt kan ligge på en linje eller at en linje kan gå gjennom et punkt. Selve om disse linjene blir vanligvis fremstilt som rette streker i en tegning, betyr ikke det nødvendigvis at de er fylt opp med punkter. Geometrien i dette planet er derfor et eksempel på en insidensgeometri. De grunnleggende postulatene kan nå sammenfattes som:
- For to forskjellige punkt eksisterer det en unik linje som går gjennom begge punktene.
- For to forskjellige linjer eksisterer det et unikt punkt som ligger på begge linjene.
- Det eksisterer fire ulike punkter slik at det ikke finnes noen linje som er insident med mer enn to av dem.
Her er det første postulatet det samme som i euklidsk geometri. Det andre postulatet sier at alle linjer skjærer hverandre slik at det projektive planet har ingen parallelle linjer og er derfor mer generelt enn det affine planet. Det tredje postulatet kreves for å unngå degenererte spesialtilfeller som ikke har noen interesse. Uten det kunne man for eksempel tenke seg en situasjon hvor alle punktene ligger på en og samme linje.
Det euklidske planet kan utvides til å bli et projektivt plan ved å addere et ideelt punkt for hver retning med parallelle linjer. Dette ligger på en måte uendelig langt borte, men vil ha like stor betydning som alle andre punkt. To forskjellige, ideelle punkt vil definere en ny, ideell linje som på samme måte må ligge uendelig langt borte.
Med denne utvidelsen av det euklidske planet er det viktig å legge merke til at hver slik parallell retning kun definerer et ideelt punkt, da man i utgangspunktet kunne tenke seg at linjene kunne skjære hverandre i begge endene uendelig langt borte. Det betyr at enten man beveger seg i den ene eller andre retningen langs en linje, så kommer man til det samme, ideelle punktet i det projektive planet.
Homogene koordinater[rediger | rediger kilde]
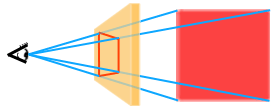
Fra de tre postulatene kan man i prinsippet utlede alle egenskaper til det projektive planet ved rent logiske argument. Dette kalles vanligvis for syntetisk geometri som da blir en ren logisk konstruksjon. Alternativt kan egenskapene undersøkes som i analytisk geometri ved å bruke koordinater. Disse ble innført av August Möbius og Julius Plücker i tiden rundt 1830.
En naturlig koordinatisering av det reelle, projektive planet RP2 er basert på dannelsen av et bilde under en perspektivisk avbildning hvor lysstråler fra et objekt sendes mot øyet og gir en avbildning i et todimensjonalt plan som ligger mellom objektet og øyet. Alt dette befinner seg i et tredimensjonalt, euklidsk rom E3 med kartesiske koordinater (x,y,z). Øyet er i origo, og bildeplanet ligger utenfor dette. Lyset fra et punkt på objektet følger da en rett linje til øyet og treffer dette med en retning som kan angis ved en vektor x = (x1,x2,x3). Dette er en sentralprojeksjon som kalles også for en lineær perspektivitet.
Denne retningsvektoren bestemmer også hvor lysstrålen går gjennom bildeplanet og kan brukes til å angi hvert punkt i dette planet. Da retningen til vektoren ikke forandres ved at den multipliseres med en konstant λ ≠ 0, vil vektorene (x1,x2,x3) og (λx1, λx2,λx3) angi ett og samme punkt. Derfor vil for eksempel (12,-8,10) angi samme punkt som (-6,4,-5). Med denne ekvivalensen kan man etablere homogene punktkoordinater i det projektive planet. For alle reelle verdier av disse tre koordinatene finnes det et tilsvarende punkt i planet, bortsett fra punktet (0,0,0) som ikke angir noen retning i det euklidske rommet.
Linjekoordinater[rediger | rediger kilde]
I denne realiseringen av det projektive planet vil en linje fremkomme som skjæringslinjen mellom et plan i E3 som går gjennom origo, og billedplanet. Ligningen for et slikt plan er ax + by + cz = 0 hvor de tre koeffisientene a, b og c er komponentene til en vektor n som står normalt på planet. Linjen i det projektive planet er entydig bestemt av denne vektoren. Hver slik linje kan derfor koordinatiseres som n = [n1,n2,n3] hvor komponentene også nå kan ta alle reelle verdier bortsett fra [0,0,0]. Da det igjen er retningen til vektoren som er avgjørende, vil [n1,n2,n3] og [λn1,λn2,λn3] beskrive samme linje. Disse koordinatene for linjen er derfor også homogene og kalles for homogene linjekoordinater. For å skille de fra de tilsvarende punktkoordinatene, skrives de med firkantparenteser i stedet for med runde parenteser.
Insidens[rediger | rediger kilde]
For at et punkt x = (x1,x2,x3) i det projektive planet skal ligge på linjen n = [n1,n2,n3], er det nødvendig at disse to vektorene står vinkelrett på hverandre. Da er prikkproduktet x⋅n = 0 eller x1n1 + x2n2 + x3n3 = 0. Når komponentene til n er gitt, vil denne ligningen gi alle punkt som ligger på den tilsvarende linjen. Punkt som ligger på samme linje er kolineære, for eksempel punkt som oppfyller 2x1 - 3x2 + x3 = 0. Omvendt vil den samme ligningen med gitte verdier for komponentene til punktet x beskrive linjer som går gjennom dette punktet. Linjene er da kopunktuelle, som for eksempel linjene n1 + 5n2 - 2n3 = 0 som alle går gjennom punktet (1,5,-2).
Hvis man har gitt to punkt a = (a1,a2,a3) og b = (b1,b2,b3), vil det være en linje n i det projektive planet som går gjennom begge punktene. Da må både a⋅n = 0 og b⋅n = 0 være oppfylt. Linjen er derfor gitt ved kryssproduktet n = a × b. I det euklidske rommet E3 er dette vektoren som står vinkelrett på planet som a og b danner. Skrevet ut blir dermed koordinatene til linjen n = [a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1]. Ligningen for punktene på linjen er x⋅(a × b) = 0. Det betyr at tre punkt a, b og c ligger på samme linje når de homogene koordinatene oppfyller (a × b)⋅c = 0. Skriver man dette trippelproduktet ut, kan det uttrykkes ved en determinant slik at betingelsen for kolineæritet blir
- .
Som et eksempel kan man bestemme linjen som går gjennom punktene (1,-2,3) og (0,2,1). Ved direkte utregning er den gitt ved vektoren [8,1,-2] som tilsvarer ligningen 8x1 + x2 - 2x3 = 0 for linjer i punktkoordinater. Et punkt på linjen er da (1,2,5). Det tilsvarer vektoren c = a + 2b eller en annen, ekvivalent lineærkombinasjon.
Generelt kan hvert punkt på linjen som går gjennom punktene a og b angis ved en lineærkombinasjon c = αa + βb for visse verdier av koeffisientene α og β. Man da koordinatene er homogene, er dette ekvivalent med c = a + λb hvor λ = β/α. For forskjellige verdier av λ beskriver denne vektoren en rekke med punkter som ligger på linjen gjennom punktene a og b. Når λ = 0 er c = a og likedan når λ → ∞, blir c = b. For punkter på denne linjen kan parametrene (α,β) betraktes som homogene koordinater for c med referanse til punktene a og b.
På helt tilsvarende måte kan man finne et punkt som går gjennom to linjer m = [m1,m2,m3] og n = [n1,n2,n3], det vil si deres skjæringspunkt. Det er gitt ved vektoren x = m × n. En linje gjennom dette punktet har ligningen x⋅l = 0 eller x1l1 + x2l2 + x3l3 = 0 i linjekoordinater. Betingelsen for at en linje k skal gå gjennom skjæringspunktet mellom linjene m og n, er derfor (m × n)⋅k = 0 eller
- .
En bunt med linjer som går gjennom skjæringspunktet for linjene m og n er gitt ved lineærkombinasjonen k = αm + βn for forskjellige verdier av parametrene α og β. De kan også oppfattes som homogene koordinater for de forskjellige linjene i rekken definert ved referanselinjene m og n.
Regneoperasjoner med homogene koordinater forenkles ved å bruke denne vektornotasjonen for punkter og linjer. Men det er ikke alltid nødvendig eller praktisk. Vanligvis betegnes punkt i det projektive planet med store bokstaver og linjer med små. Bare når et homogent koordinatsystem foreligger, kan et punkt A angis mer presist som en vektor a med tre komponenter på samme måte som at en linje m kan spesifiseres ved en 3-komponent vektor m.
Ideelle punkt og linjer[rediger | rediger kilde]
For at en lysstråle fra et objektpunkt til øyet (origo) skal krysse et punkt i billedplanet, kan den ikke være parallell til dette planet. En vektor (x1,x2,x3) som er parallell med billedplanet vil da ikke skjære dette og tilsvarer et punkt som på et vis ligger uendelig langt borte. I det projektive planet må også disse idelle punkt tas med på samme måte som vanlige, endelige punkt. De ligger på en linje som tilsvarer et plan i E3 gjennom origo som er parallelt med billedplanet. Denne ideelle linjen er derfor beskrevet ved en vektor [n1,n2,n3] som står normalt på billedplanet.
Ved å ta med den ideelle linjen med sine ideelle punkt, er det euklidske planet utvidet til å bli et projektivt plan. I det vil alle vanlige linjer krysse den ideelle linjen i et ideelt punkt. Da to linjer kun kan ha et skjæringspunkt, vil man komme til samme, ideelle punkt uansett i hvilken retning man beveger seg langs en linje mot det uendelige fjerne. En linje mellom to ideelle punkt faller sammen med den ideelle linjen. Vanlige linjer som ser ut til å være parallelle, skjærer hverandre i et ideelt punkt.
De homogene koordinatene til de ideelle punktene og deres felles linje avhenger av hvordan billedplanet legges inn i E3. Den mest symmetriske måten er å plassere det slik at det går gjennom punktene X = (1,0,0), Y = (0,1,0) og Z = (0,0,1). Disse tre punktene definerer et referansetriangel i det projektive planet. Hvert punkt kan da angis som P = x1X + x2Y + x3Z. Normalen til billedplanet definerer nå den ideelle linjen som n∞ = [1,1,1]. Denne linjen er derfor også beskrevet ved ligningen x1 + x2 + x3 = 0. Det betyr at alle ideelle punkt x∞ har homogene koordinater som summerer seg opp til null. For eksempel er P1 = (-2,1,1) et ideelt punkt i dette koordinatsystemet.
Standard koordinatsystem[rediger | rediger kilde]

For mange praktiske oppgaver er mer hensiktsmessig å plassere bildeplanet parallelt med et av koordinatplanene i E3. Vanligvis velges det å være parallelt med xy-planet, for eksempel gitt ved z = 1. Linjen til den ideelle linjen tilsvarer da vektoren [0,0,1] slik at den er beskrevet ved ligningen x3 = 0. Punkter som har denne tredje koordinaten lik null, er da ideelle og har homogene koordinater av formen (x1,x2,0) hvor kun forholdet x1/x2 teller. I motsatt fall kan de betraktes som endelige punkt i et euklidsk plan. For et slikt punkt P = (x1,x2,x3) med x3 ≠ 0 kan da koordinatene skaleres slik at man får P = (x,y,1) hvor x = x1/x3 og y = x2/x3 blir kartesiske koordinater i den endelige, euklidske delen av det projektive planet.
Som en illustrasjon kan man betrakte den euklidske linjen x = 1. Med homogene koordinater vil den ta formen -x1 + x3 = 0 som tilsvarer vektoren [-1,0,1] i linjekoordinater. Likedan vil vektoren [-1,0,3] tilsvare den euklidske linjen x = 3. Kryssproduktet av disse to vektorene gir det ideelle punktet (0,1,0) som er skjæringspunktet mellom disse to parallelle linjene og ligger i det uendelige fjerne.
På samme måte finner man ved bruk av regnereglene for homogene koordinater at skjæringspunktet for de to parallelle linjene ax1 + bx2 + cx3 = 0 og ax1 + bx2 + c' x3 = 0 er punktet (c' - c)(b, -a, 0) som er ekvivalent med (b, -a, 0). Som ventet har det x3 = 0 og er derfor et ideelt punkt i samme retning som linjene går.
I dette koordinatsystemet er origo punktet (0,0,1) som tilsvarer n3 = 0 i linjekoordinater. Det som i den endelige delen er x-aksen, tilsvarer linjen x2 = 0 i det fulle, projektive planet. De homogene koordinatene til denne linjen er [0,1,0]. På samme måte tilsvarer y-aksen linjen x1 = 0 gitt ved vektoren [1,0,0]. Den tredje koordinataksen er linjen x3 = 0 i det uendelige gitt ved vektoren n∞ = [0,0,1]. Alle ideelle punkt x∞ = (x,y,0) ligger på denne. Som referansetriangel i planet kan nå punktene X1 = (1,0,0), X2 = (0,1,0) og X3 = (0,0,1) benyttes. To av disse er nå ideelle, men må behandles på like fot med alle andre punkt.
Sfærisk modell[rediger | rediger kilde]

En alternativ fremstilling av det projektive planet får man ved å tenke seg at man benytter en kuleflate i stedet for et plant billedplan. Da vil hver lysstråle inn på øyet i kulens sentrum treffe overflaten i to punkter. Bare et av disse må benyttes for å angi lysstrålens retning. Man kan da for eksempel betrakte hvert punkt på den nordlige halvkulen som et punkt i det projektive planet. Med det valget vil den ideelle linjen tilsvare punkter langs ekvator hvor motsatte motsatte punkt representerer det samme, projektive punktet. Prøver man å lage en fysisk modell av dette sfæriske koordinatsystemet, vil man ikke klare det i vårt tredimensjonale rom da den halve kuleflaten må skjære gjennom seg selv. Man kan kun tenke seg dette i et rom med ekstra dimensjoner.
Denne halve kuleflaten kan man videre tenke seg blir skviset sammen til en sirklulær disk hvor motsatte punkt på randen må identifiseres og tilsvarer den ideelle linjen. Topologisk er denne disken det samme som et kvadrat hvor motsatte sider må vris og limes sammen. Dette kan kun gjøres hvis man hadde adgang til et rom med en høyere dimensjon. Dette gir en ny, mer abstrakt modell for det projektive planet.
Dualitet[rediger | rediger kilde]
Allerede i de fundamentale postulatene er det en symmetri mellom punkt og linjer i det projektive planet. To punkt definerer alltid en linje, mens to linjer definerer et entydig punkt. Denne symmetrien kalles en dualitet mellom punkt og linjer i planet og forblir intakt når man så betrakter mer kompliserte situasjoner. Et punkt er dual til en linje, mens en linje er dual til et punkt. For hver geometrisk konstellasjon av n punkt og m linjer, vil det eksistere en dual konstellasjon med m punkt og n linjer.

Denne dualiteten sees også når homogene koordinater blir benyttet. Hver geometrisk sammenheng kan uttrykkes som en ligning i punktkoordinater, linjekoordinater eller begge deler. For en ligning som involverer kun punktkoordinater, finnes det en dual ligning som inneholder bare linjekoordinater og omvendt. Ligningen x1n1 + x2n2 + x3n3 = 0 er selvdual da den går over i seg selv under en slik dualisering. Det tilsvarer at den kan beskrive enten punkter på linjen [n1,n2,n3] eller linjer gjennom punktet (x1,x2,x3).
En trekant er gitt ved tre punkt A, B og C som ikke ligger på samme linje. Disse kan forbindes med tre linjer a = BC, b = CA og c = AB som er sidene i trekanten. I motsetning til det som er vanlig i euklidsk geometri, ender ikke sidene i de gitt hjørnene i det projektive planet, men går gjennom disse og fortsetter i prinsippet mot uendelig i begge retninger.
Den duale trekanten er på tilsvarende vis definert ved tre linjer a, b og c som ikke går gjennom samme punkt. Linjene skjærer hverandre i tre punkt som kan kalles A = b⋅c, B = c⋅a og C = a⋅b hvor for eksempel b⋅c står for skjæringspunktet mellom linjene b og c etc. Men denne dualiseringen har nå gitt akkurat samme geometriske konstellasjon av punkter og linjer som i første tilfelle med tre gitte punkt. Derfor er trekanten selvdual i projektiv geometri.
Duale firkanter[rediger | rediger kilde]

Mens en vanlig firkant har fire hjørner og fire sider som er endelige linjestykker gjennom disse, er en fullstendig firkant definert ved fire linjer og vil gi opphav til i alt seks skjæringspunkt som er dens hjørner. På samme måte kan man definere et fullstendig kvadrangel ved fire punkter som kan forbindes med i alt seks linjer. Derfor vil en firkant definert ved fire hjørner prinsipielt være forskjellig fra en som er definerte ved fire sider. Den ene er dual til den andre.

Hvis man kaller de fire hjørnene i et fullstendig kvadrangel for A, B, A' og B' , kan disse forbindes med seks linjer AA' , AB, AB' , BA' , BB' og A'B' . Disse vil skjære hverandre i tre nye punkter, D = AB⋅A'B', E = AA'⋅BB' og F = AB'⋅A'B som kalles diagonale punkt. Sammen danner disse nye punktene et diagonalt triangel i denne generaliserte firkanten.
På samme måte vil en fullstendig firkant være definert ved fire linjer a, b, c og d. Disse gir opphav til seks hjørner a⋅b, a⋅c, a⋅d, b⋅c, b⋅d og c⋅d. Forbindes to og to motsatte hjørner, fremkommer tre diagonale linjer som igjen danner en diagonal trekant.
Disse to geometriske konstellasjonene er duale til hverandre. Begge to spiller en sentral rolle i det projektive planet. For eksempel, så vil to hjørner og to skjæringspunkt med diagonalene på en og samme side i hvert slikt kvadrangel være harmonisk konjugerte. Likedan vil hver side i den diagonale trekanten skjæres av sider i kvadranglet. Disse fire punktene er også harmonisk konjugerte. Dette var allerede kjent for Pappos og videre utviklet av Desargues.
Desargues' teorem[rediger | rediger kilde]

I det projektive planet er Desargues' teorem av grunnleggende betydning. Den sier at når linjer gjennom tilsvarende hjørner i to trekanter går gjennom et punkt, vil de tilsvarende sidene i trekantene skjære hverandre i punkt som ligger på en linje. Man sier at trekantene ligger i et perspektiv med et senter hvor linjene gjennom hjørnene møtes og en akse hvor skjæringspunktene mellom sidene ligger.
Teoremet kan bevises på mange forskjellige måter, avhengig av det aksiomatiske grunnlaget. Mest direkte følger det fra en formulering basert på bruk av reelle, homogene koordinater. Hvis den en trekanten er gitt ved punktene A, B og C, mens den andre er gitt ved A' , B' og C' , antas de tre linjene AA' , BB' og CC' å gå gjennom et felles punkt S. På disse tre linjer kan man nå velge koordinater slik at man kan skrive S = A + A' , S = B + B' og S = C + C' . Fra de to første uttrykkene følger at A - B = B' - A' . Nå er A - B et punkt på linjen gjennom hjørnene A og B på samme måte som B' - A' er et punkt på linjen gjennom hjørnene A' og B' . Dette felles punktet må derfor være skjæringspunktet R mellom linjene, det vil si R = A - B. På samme måte er skjæringspunktet mellom linjene BC og B'C' gitt som P = B - C, mens skjæringspunktet mellom linjene CA og C'A' er Q = C - A. Men koordinatene til disse tre skjæringspunktene sees nå å oppfylle relasjonen P + Q + R = 0 som betyr at de er lineært avhengige slik at de tre punktene ligger på en og samme linje.
I denne formuleringen av beviset for Desargues' setning er den avgjørende antagelsen at man kan konkludere at A - B = B' - A' fra A + A' = B + B' . Det betyr at den tallkroppen koordinatene tilhører, må være assosiativ som for de reelle tallene. Hvis ikke, gjelder ikke lenger Desargues' setning.
Pappos' teorem[rediger | rediger kilde]

Teoremet som i dag blir omtalt som Pappos' teorem ble formulert for snart to tusen år siden av Pappos fra Alexandria. Han viste det ved hjelp av euklidsk geometri. Men da det kun omhandler linjer mellom skjæringspunkt mellom andre linjer, har det større gyldighet og er av grunnleggende betydning i projektiv geometri.
Man har gitt en linje med tre punkt A, B og C samt en annen linje med punktene A' , B' og C' . Da vil skjæringspunktet mellom linjene AB' og BA' , skjæringspunktet mellom AC' og CA' samt skjæringspunktet mellom BC' og CB' ligge på en og samme linje som kalles Pappos-linjen. Dette resultatet er uavhengig av hvordan punktene ordnes på de to linjene.
For å bevise setningen kan man igjen benytte homogene koordinater. I det projektive planet vil linjene skjære hverandre i et felles punkt P. På den første linjen kan man benytte dette punktet samt punktet A som referansepunkt. Da vil man kunne skrive B = P + A og C = λP + A. Likedan velger man P og A' som referansepunkt på den andre linjen slik at B' = P + A' og C' = λ'P + A' .
Da skjæringspunkt K er mellom linjene AB' og BA' , må koordinatene til dette punktet kunne skrives som (P + A') + A eller (P + A) + A' . Derfor har man ganske enkelt at K = P + A + A' . På samme måte må koordinatene for skjæringspunktet L mellom linjene AC' og CA' skrives som en tilsvarende lineærkombinasjon mellom koordinatene til disse punktene. Det medfører at L = λλ'P + λA' + λ'A = λ(λ'P + A') + λ'A = λ'(λP + A) + λA' .
Et bestemt punkt M på linjen mellom K og L har nå koordinatene M = K - L. Utregnet gir det M = (1 - λ')(P + A) + (1 - λ)(λ'P + A') = (1 - λ)(P + A') + (1 - λ')(λP + A). Men det betyr at dette punktet M også er skjæringspunktet mellom linjene BC' og CB' . Derfor ligger de tre skjæringspunktene K, L og M på samme linje.
I dette algebraiske beviset for Pappos' setning inngår det ikke noe sted hvordan punktene på de to linjene er ordnet seg i mellom. Det er derfor uavhengig av dette. Men for hver ordning vil den tilsvarende Pappos-linjen være forskjellig.
Ser man nøyere på det samme beviset, oppdager man også at det er nødvendig å ha λ'λ = λλ' . De homogene koordinatene som benyttes i det projektive planet må derfor tilhøre en tallkropp som er kommutativ, det vil si at faktorenes rekkefølge ikke er viktig.
Dual versjon[rediger | rediger kilde]
I projektiv geometri har hvert utsagn en dual versjon. For det projektive planet arter denne dualiseringen seg ved ombytte av punkt og linje slik at to punkter definerer en linje, mens to linjer definerer et punkt. Den duale versjon av Pappos tar derfor utgangspunkt i to gitte punkt. Gjennom det ene går linjene a, b og c, mens gjennom det andre går linjene a' , b' og c'. Da definerer skjæringspunktene a⋅b' og b⋅a' en linje k, skjæringspunktene a⋅c' og c⋅a' en linje l, mens skjæringspunktene b⋅c' og c⋅b' definerer en linje m. Pappos' duale teorem sier da at disse tre linjene k, l og m går gjennom samme punkt. Det kan bevises på en helt analog måte som i den første versjonen.
Pascals teorem[rediger | rediger kilde]

Som 16-åring publiserte Blaise Pascal i 1639 en generalisering av Pappos' teorem til å gjelde for seks punkt plassert på et vilkårlig kjeglesnitt. Når disse forbindes med linjer, vil de forme et heksagon. Teoremet til Pascal sier nå at motsatte sider i dette polygonet vil skjære hverandre i tre punkt som ligger på en linje. Den kalles Pascal-linjen.
Da seks punkt kan danne e heksagon på seksti forskjellige måter ved å trekke linjer mellom punktene, vil det da for disse seks gitte punktene kunne lages seksti forskjellige Pascal-linjer. Disse nye linjene gir igjen opphav til nye skjæringspunkt med spesielle egenskaper. Av denne grunn fikk konstellasjonen med seks punkt på et kjeglesnitt senere navnet Hexagrammum Mysticum.
Fra Pascals teorem kan man utlede mange nye setninger i spesielle tilfeller når for eksempel to punkt på kjeglesnittet faller sammen. Når kjeglesnittet degenererer til to linjer, går teoremet over i Pappos' teorem.
Den duale versjonen av Pascals teorem, heter Brianchons teorem. Det sier at når et kjeglesnitt er omskrevet med seks tangentlinjer, vil diagonalene som forbinder motsatte hjørner i heksagonet som linjene danner, gå gjennom ett og samme punkt.
Projektive transformasjoner[rediger | rediger kilde]
Hvis man betrakter det projektive planet som innlagt i det tredimensjonale rommet E3, vil de homogene koordinatene xμ = (x1,x2,x3) for et punkt x avhenge av dets plassering i forhold til koordinataksene. Forandres dets posisjon, vil koordinatene for hvert punkt også forandres eller transformeres. Da dette vil være lineære transformasjoner, vil de alminnelighet kunne skrives som x' 1 = a11x1 + a12 x2 + a13 x3 og tilsvarende for de to andre koordinatkomponentene. På matriseform kan disse tre uttrykkene sammenfattes som
eller mer kompakt som x' = A⋅x hvor 3×3 matrisen A inneholder 9 elementer som parametriserer transformasjonen. De tre koordinatene til punktet x inngår her i en kolonnematrise. Da disse koordinatene er homogene, kan alle elementene i transformasjonsmatisen A skaleres med samme faktor. Derfor inneholder den bare 8 fri parametre. De er fullstendig bestemt hvis man angir koordinatene til fire punkt før og etter transformasjonen. Det er fordi hvert punkt inneholder to frie variable.
Slik transformasjonen er beskrevet her, er det en passiv transformasjon da det er planets orientering i forhold til det omsluttende rommet som forandres. Men den vil ha samme form hvis den betraktes som en aktiv transformasjon ved at planets orientering er uforandret, men selve punktets posisjon i planet forandres.
Uansett interpretasjon, er dette formen for den mest generelle projektive transformasjonen. Den kalles også for en kollineasjon da den transformerer kollineære punkt på en linje til en rekke med kollineære punkt på en transformert linje. Det kan man se fra ligningen n⋅x = 0 for en slik linje før transformasjonen. Her må vektoren n for linjen da betraktes som en linjematrise, altså hvor komponentene [n1,n2,n3] inngår horisontalt. Setter man så inn den inverse transformasjonen x = A -1⋅x' i ligningen for linjen, forandres den til n⋅A -1⋅x' = 0. Etter transformasjonen er derfor linjen gitt som n'⋅x' = 0 med nye linjekoordinater n' = n⋅A -1. De transformerer derfor med den inverse matrisen.
Hvis den endelige delen av det projektive planet defineres ved x3 ≠ 0, vil en kollineasjon indusere en tilsvarende transformasjon mellom de euklidske komponentene x = x1/x3 og y = x2/x3. Den blir da ikke-lineær og får den eksplisitte formen
Det er slik den benyttes i billedkunst som fotografi og datagrafikk, for å gi perspektiv i bildet. Mest vanlig er det da å benytte et sentralperspektiv, som tilsvarer en mer spesialisert kollineasjon med 6 frie parametre i alminnelighet.
Affine transformasjoner[rediger | rediger kilde]
Når man betrakter den endelige delen av det projektive planet med x3 ≠ 0 og kun kollineasjoner med a31 = a32 = 0, vil ikke koordinaten x3 forandres. Man kan da sette x3 = 1 og velge a33 = 1 . Den generelle transformasjonene tar den mer spesielle formen
Dette representerer en affin transformasjon. Det projektive planet kan på denne måten begrenses til å ha egenskaper i overensstemmelse med affin geometri. Den ideelle linjen x3 = 0 holdes da fast. To linjer som skjærer denne i samme punkt, sies å være parallelle. Og eksistensen av parallelle linjer er hva som karakteriserer et affint rom.
Korrelasjoner og polariteter[rediger | rediger kilde]
Mens en projektiv transformasjon fra punkt til punkt eller fra linje til linje, kalles en kollineasjon, blir en lineær transformasjon fra et punkt til en linje (eller omvendt) omtalt som en korrelasjon. Matematisk kan en slik transformasjon fra et punkt x til en linje m skrives som mT = B⋅x hvor B er en 3×3 matrise. Her er mT den transponerte av linjematrisen m og derfor en kolonnematrise. Punkter på en linje transformeres til linjer gjennom et punkt. På samme måte transformes en linje n til et punkt yT = n⋅B -1. For at den inverse matrisen B -1 skal kunne beregnes, må determinanten |B | ≠ 0. Denne transformasjonen tar linjer gjennom et punkt til punkt på en linje.
Pol og polare[rediger | rediger kilde]
Hvis en korrelasjonen tar et punkt til en linje, vil denne linjen i alminnelighet ikke bli transformert tilbake til samme punkt. For at det skal kunne skje må den tilsvarende transformasjonsmatrisen C være symmetrisk. Da er Cij = Cji som betyr at C = CT. Korrelasjonen kalles nå for en polaritet. Det er da vanlig å kalle linjen mT = C⋅x for polaren til punktet xT = m⋅C -1 som igjen kalles for polen til linjen m.
Gitt to punkt x og y , vil en polaritet C gi opphav til to polarer mT = C⋅x og nT = C⋅y . Hvis nå x ligger på polaren til y, vil n⋅x = 0. Men nå er n = yT⋅C slik at ligningen for polaren kan skrives som xT⋅C⋅y = 0 etter transponering. Da dette er lik med m⋅y = 0, betyr det også at punktet y ligger på polaren til x. To slike punkt sies å være konjugerte.
Fra dette følger at når et punktet beveger seg langs polaren til et annet punkt, vil polaren til det første punktet rotere rundt polen til det andre. Dette er innholdet av et teorem som var kjent på midten av 1600-tallet. Det tilskrives vanligvis La Hire som var influert av arbeidene til Desargues og Pascal.
Kjeglesnitt[rediger | rediger kilde]
I den vanlige beskrivelsen av pol og polare inngår et kjeglesnitt i stedet for en polaritet som i denne projektive fremstillingen. Men disse to begrepene er ekvivalente da et kjeglesnitt er det geometriske stedet for de punkt som ligger på sin egen polare. Punktene er derfor selvkonjugerte og oppfyller ligningen xT⋅C⋅x = 0. Skrives den eksplisitt ut, blir den
Hvis man bare betrakter den endelige delen av det projektive planet, er x3 ≠ 0. Man kan da innføre de euklidske koordinatene x = x1/x3 og y = x2/x3, og ligningen går over til den vanlige formen for et kjeglesnitt.
Linjekoordinatene for polaren til et punkt y med hensyn på et kjeglesnitt med polaritet C er nå n = yT⋅C. Ligningen n⋅x = 0 for polaren blir dermed yT⋅C⋅x = 0. Dette gjelder også for det spesielle tilfellet at y er et punkt på denne kurven. Den tilsvarende polaren er da tangent til kjeglesnittet i dette selvkonjugerte punktet. Ligningen for polarer og tangenter har derfor akkurat samme form.
Ligningen xT⋅C⋅x = 0 for et kjeglesnitt bestemmer de selvkonjugerte punktene x som ligger på kurven. Man kan alternativt beskrive det samme kjeglesnittet i linjekoordinater m = xT⋅C for tangentene til hvert selvkonjugert punkt. Den nye ligningen blir da m⋅C -1⋅mT = 0 og beskriver en skare med selvkonjugerte linjer eller tangenter som omhyller kjeglesnittet.
Ved en projektiv transformasjon av koordinatene vil kjeglesnittet i alminnelighet forandres. For eksempel kan en sirkel forandres til en ellipse. Men det kan også forandre type som at en parabel forandres til en ellipse som igjen kan transformeres til en hyperbel. Ser man bort fra degenererte kjeglesnitt bestående av et par linjer, finnes det bare to grunnleggende kjeglesnitt i det projektive planet. Det første er gitt ved ligningen
men er rent abstrakt da det ikke inneholder noen fysiske punkter beskrevet ved reelle koordinater. Den tilsvarende polariteten C sies å være elliptisk og tilsvarer enhetsmatrisen. Sammenhengen mellom pol og polare er da veldig enkel da de har de samme, homogene koordinatene. Hvis polen for eksempel har punktkoordinatene (1, -2, 3), er polaren gitt ved linjekoordinatene [1, -2, 3]. Dette forklarer også opphavet til navnene pol og polare. I modellen hvor det projektive planet er lagt inn i E3, er nå polen til en linje gitt ved normalen til planet som definerer den på samme måte som i sfærisk eller elliptisk geometri.
Den andre, fundamentale polaritet er gitt ved
om sies å være hyperbolsk. Det tilsvarende kjeglesnittet har nå reelle punkter i det projektive planet RP2. Avhengig av hvordan den ideelle linjen legges, kan dette beskrive en ellipse, parabel eller hyperbel. Historisk spilte det en viktig rolle i den matematiske beskrivelsen av hyperbolsk geometri som ble gitt av Felix Klein.
Konstruksjon av pol og polare[rediger | rediger kilde]

Hvis man har gitt to punkt x og y liggende på et kjeglesnitt, vil tangentene i disse punktene skjære hverandre i et punkt z. Dette ligger derfor på polarene til x og y. Men fra den generelle sammenhengen mellom pol og polare, følger det også at begge punktene ligger på polaren til z. Den kan derfor finnes ved en geometrisk konstruksjon hvor man trekker en rett linje gjennom de to punktene x og y. Polaren til et punkt utenfor kjeglesnittet kan derfor finnes ved denne konstruksjonen såfremt man kan konstruere tangentene.
Omvendt kan polen til en linje som skjærer kjeglesnittet, finnes på samme måte ved å konstruere tangentene i de to skjæringspunktene. Polen er da skjæringspunktet mellom tangentene. Dette kan så igjen benyttes til å finne polaren til et punkt innenfor kjeglesnittet ved å trekke to vilkårlige linjer gjennom det. Polaren er da linjen gjennom polene til de to linjene og er uavhengig av deres valg.
Fullstendig firkant på kjeglesnitt[rediger | rediger kilde]

Svakheten i denne metoden til bestemmelse av pol og polare, ligger i den geometriske konstruksjonen av tangentene til kjeglesnittet. Det kan ikke bli gjort helt nøyaktig kun ved bruk av linjal og passer. Denne vanskeligheten kan omgås ved benytte en viktig egenskap ved en fullstendig firkant som har fire hjørner på kjeglesnittet. Den diagonale trekanten til firkanten er da «selvpolar» på den måten at hvert av dens tre hjørner er polen til den motsatte siden i trekanten. Er kjeglesnittet en sirkel, vil firkanten være en syklisk.
Basert på denne egenskapen kan man finne polaren til et punkt z ved å trekke to vilkårlige linjer gjennom punktet slik at de begge skjærer kjeglesnittet. Linjene er derfor sekanter. De fire skjæringspunktene definere en fullstendig firkant hvor to av sidene er disse sekantene. To andre, motstående sider i firkanten skjærer hverandre i det diagonale punktet x, mens de to siste sidene skjærer hverandre i et punkt y. Sammen med det gitte punktet z utgjør disse tre punktene hjørnene i den dagonale trekanten. Polaren til z er da linjen gjennom punktene x og y. Den er uavhengig av hvilke to sekanter som opprinnelig ble valgt til å forme fden fullstendige irkanten på kjeglesnittet.
Fra samme konstruksjonen ser man også at polaren til punktet x er linjen gjennom de diagonale punktene y og z. Det kan benyttes til å finne polaren til et punkt som ligger innenfor kjeglesnittet. Igjen trekker man to vilkårlige sekanter gjennom punktet for å finne en firkantl liggende på kjeglesnittet. De to andre diagonale punktene blir liggende utenfor kjeglesnittet og dermed også polaren til det gitte punktet.
Omvendt kan denne direkte fremgangsmåten også benyttes til å konstruere polen til en gitt linje. Man velger da et vilkårlig punkt på linjen og trekker to sekanter gjennom dette. Skjæringspunktene med kjeglesnittet definerer en fullstendig firkant. Polen til linjen er da det diagonale punktet til dette som ligger utenfor den gitte linjen.
Andre projektive plan[rediger | rediger kilde]
Det reelle, projektive planet RP2 har homogene koordinater (x1,x2,x3) som tilhører den reelle tallkroppen R. Andre projektive plan KP2 kan defineres på samme måte ved å la de homogene koordinatene tilhøre en annen tallkropp K. Det enkleste eksemplet er det komplekse, projektive planet CP2 basert på tallkroppen C bestående av komplekse tall z = x + iy. Her er x og y reelle tall og i = √-1 er den imaginære enhet. Dette planet har to komplekse dimensjoner som tilsvarer fire vanlige dimensjoner. I tillegg til sine geometriske egenskaper, er det også av interesse innen teoretisk fysikk hvor det kan benyttes til å konstruere forskjellige kvantefeltteorier.
Endelige plan[rediger | rediger kilde]
Et endelig, projektivt plan FP2 er basert på en endelig tallkropp, også kalt en Galois-kropp. Inneholder denne n elementer, betegnes den som Fn, mens det tilsvarende projektive planet kalles ofte PG(2,n). Tallet n sies å være planets orden. De homogene koordinatene (x1,x2,x3) kan da bare ta et visst antall forskjellige verdier slik at dette planet inneholder bare et endelig antall punkter og et like stort antall linjer. Planet sies derfor å være endelig.
Gjennom hvert punkt vil det gå et visst antall linjer som er like stort som antall punkt på hver linje. Hver linje vil som i alle projektive plan, skjære hverandre i kun et punkt. Selv om antall punkt på hver linje er endelig, tegnes de ofte likevel som kontinuerlige streker. Mer abstrakt kan man angi en linje med de punktene den inneholder.
Planets orden n bestemmer hvor mange punkt og linjer det finnes i planet. Dette antallet kan finnes ved å beregne antall endelige punkt pluss antall punkt på linjen i det uendelige. De ideelle punktene på denne linjen har koordinater av formen (x1,x2,0). Siden disse er homogene, kan man skalere den andre koordinaten slik at den blir lik 1. Antall punkt med koordinater av formen (x1,1,0) er nå n tilsvarende antall verdier x1 kan ta. I tillegg kommer tilfellet at x2 = 0 som tilsvarer det ene punktet (1,0,0). I alt er det derfor n + 1 punkter på denne linjen. Og da denne er ekvivalent med alle andre linjer, vil alle inneholde et slikt antall punkter. Dualitet sier nå at n + 1 vil også være antall linjer gjennom hvert punkt.
De endelige punktene i planet har koordinater av formen (x1,x2,1). Her kan både x1 og x2 fritt ta n verdier slik at det er i alt n 2 slike endelige punkt. Da disse punktene utgjør et affint plan, er dette det totale antall punkter i det affine planet basert på denne tallkroppen. Men det projektive planet inneholder i tillegg n + 1 punkter i det uendelige som gir til sammen n 2 + n + 1. Dualitet sier at dette også er antall linjer i dette planet.
Når n = 1, inneholder planet bare tre punkter. Dette er ikke nok til å gi et fullt, projektivt plan som oppfyller de tre aksiomene. Derfor må n ≥ 2. Teorien for endelige Galois-kropper sier at n = pk hvor p er et primtall og k et positivt heltall. Man kan derfor konstruere slike endelige plan for n = 2,3,4,5,7,8,9,11,13 og så videre. Matematikere har lagt ned store anstrengelser i å forstå hvorfor projektive plan av orden n = 6 og n = 10 ikke kan konstrueres.
Eksempel: Syvpunktsplanet[rediger | rediger kilde]
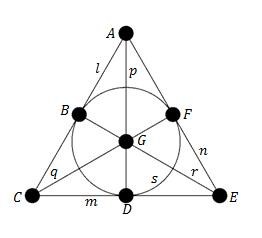
Det minste, ikke-trivielle projektive planet er av orden n = 2 basert på Galois-kroppen F2. Den er identisk med de binære tallene (0,1) under addisjon og multiplikasjon. Dette endelige planet inneholder syv punkter med homogene koordinater (1,0,0), (0,1,0), (0,0,1), (1,1,0), (1,0,1), (0,1,1) og (1,1,1). Tilsvarende kan koordinatene for de syv linjene angis. Vanligvis omtales som «syvpunktsplanet» eller «Fano-planet» etter den italienske matematiker Gini Fano som systematiske undersøkte slike endelige plan. Det opptrer i teorien for oktonioner.
Planet er illustrert i figuren til høyre. De syv punktene er angitt som A, B, C, D, E, F og G. Tilsvarende er de syv linjene angitt som l, m, n, p, q, r og s. Hver linje inneholder tre punkter, mens tre linjer går gjennom hvert av punktene. Strekene mellom punktene på samme linje er bare trukket som illustrasjon. Det har ingen betydning om disse er trukket som rette eller krumme linjer.
Man kan velge å betrakte linjen s som linjen i det uendelige med tre ideelle punkt B, D og F. Fjernes disse, står man igjen med fire endelige punkt og seks linjer som forbinder dem. Dette er det affine planet av orden n = 2. Det tilsvarer punkter og linjer som utgjør et tetraeder.
Se også[rediger | rediger kilde]
Litteratur[rediger | rediger kilde]
- J.W. Russell, An elementary treatise on pure geometry with numerous examples, Clarendon Press, Oxford (1893).
- J. W. Young, Projective Geometry, The Mathematical Association of America (1930).
- D.N. Lehmer, An Elementary Course in Synthetic Projective Geometry, Guthenberg Ebook (2005).
- D.J. Struik, Lectures on Analytic and Projective Geometry, Dover Publications, New York (2011). ISBN 0-486-48595-1.
- H.S.M. Coxeter, Projective Geometry, Springer-Verlag, New York (1987). ISBN 978-0-387-40623-7.
Eksterne lenker[rediger | rediger kilde]
- S. Birchfield, An Introduction to Projective Geometry, Stanford lectures, for computer vision.
- T. Peil, Plane Projective Geometry Arkivert 6. mars 2016 hos Wayback Machine., webpages, Minnesota State University.
- TU, Berlin, Projective Geometry, lectures notes for course Geometry I (2012).








