Sfærisk trekant

Sfærisk trekant med hjørner A, B og C samt motstående sidekanter a, b og c.

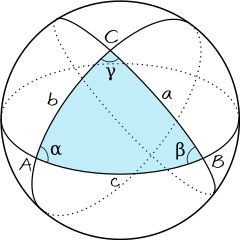
En sfærisk trekant er en trekant på overflaten av en kule. Den ligger slik at dens sider utgjøres av storsirkler på kuleflaten. Hjørnene i trekanten er gitt ved skjæringspunkter mellom storsirklene og betegnes med A, B og C i figuren til høyre. Den indre vinklen til trekanten i hjørnet A betegnes med den greske bokstaven α. Det er den dihedral vinkelen mellom de to planene som inneholder storsirklene gjennom punktet A. Det tilsvarer vinkelen mellom de to tangentene i det samme punktet langs sirkelbuene AB og AC. På samme måte er trekantvinklene β og γ definert. Er en av disse hjørnevinklene lik 90°, kalles trekanten for rettvinklet.

Sidekantene til en trekant på en kuleflate er gitt ved de tilsvarende sentralvinklene fra kulens sentrum.

Siden AB i trekanten er motsatt hjørnet C. Sett fra sentrum i kulen spenner den ut en vinkel som betegnes med den latinske bokstaven c. Er radius i kulen R, er lengden av denne trekantsiden AB = c⋅R. På samme måte er BC = a⋅R og CA = b⋅R. Ofte angis størrelsen på sidene i trekanten kun ved vinklene a, b og c som i figuren. Det tilsvarer at man betrakter en sfærisk trekant på en kule som har radius R = 1. I denne notasjonen sies en sfærisk trekant med minst en sidekant lik 90° å være rettsidet.

For hvert av hjørnepunktene i trekanten er det tre antipodale skjæringspunkt A' , B'  og C'  som ligger diametralt motsatt hjørnene A, B og C. Trekanten A'B'C' kalles den inverse trekanten til ABC. Det er i alt seks slike skjæringspunkt mellom tre storsirkler slik at de gir til sammen åtte trekanter på kuleflaten. De resterende seks er A'BC, AB'C, ABC' , A'B'C, AB'C'  og A'BC' . Størrelsen av de indre vinklene i disse trekantene vil hver ligge mellom 0° og 180°. Summen av vinklene i en trekant må derfor være mindre en 540°. Den må også være større enn 180° som man kan se ved å la den ene vinkelen i trekanten bli veldig liten. Det tilsvarer at vinkelsummen α + β + γ ligger mellom π og 3π radianer. Fra kravet om at hver hjørnevinkel skal være mindre enn π, følger at hver side i trekanten også må være mindre enn π. Derfor kan ikke summen a + b + c av sidelengdene i trekanten overstige 3π  når de måles i vinkelenheter. Læren om sammenhengen mellom vinkler, sider og areal i en sfærisk trekant kalles sfærisk trigonometri.

Trekantareal

Tre storsirkler deler en kuleflate opp i åtte sfæriske trekanter.

Arealet til trekanten ABC i figuren til høyre kan beregnes ut fra arealet 4π R² til hele kuleflaten samt bruk av formelen 2φR² for arealet av hver sfærisk tokant med dihedral åpningsvinkel φ som de tre storsirklene deler kuleflaten er opp i.

Tokanten med hjørner A og A'  og åpningsvinkel α har arealet S_α = 2αR². Den består av trekanten ABC pluss trekanten A'BC. Arealet til denne er lik arealet S_b til den blå trekanten AB'C'  i figuren da arealet til den inverse trekanten A'B'C'  er nøyaktig like stort som arealet S til den gitte trekanten ABC. Derfor har man at

$S_{b}=2\alpha R^{2}-S$

På samme måte er arealet av den grønne trekanten CAB'  gitt som S_g = 2βR² - S, mens den røde trekanten CA'B'  har arealet S_r = 2γR² - S.

Storsirkelen som går gjennom punktene A, C, A'  og C'  deler hele kuleflaten i to halvdeler, hver med arealet 2πR². Den øverste av disse i figuren består av den blå, grønne og røde trekanten pluss den inverse trekanten A'B'C' . Da denne siste også har arealet S, må man ha at den enkle ligningen 2πR² = S_b + S_g + S_r + S skal være oppfylt. Setter man her inn for arealene til de tre første trekantene, følger det at

$S=(\alpha +\beta +\gamma -\pi )R^{2}$

er arealet av den sfæriske trekanten. Da dette alltid må være positivt, ser man enda en gang at summen av de indre vinklene i en sfærisk trekant må være større enn 180°. Dette er i motsetning til vinklene i en euklidsk trekant hvor summen av vinklene alltid er nøyaktig 180°.

Differansen E = α + β + γ - π  kalles ofte for den sfæriske eksessen for trekanten på kuleflaten. Ved bruk av sfærisk trigonometri kan den beregnes direkte fra lengdene a, b og c til sidene i trekanten. Det gir

$\tan {E \over 4}={\sqrt {\tan {\frac {s}{2}}\cdot \tan {\frac {s-a}{2}}\cdot \tan {\frac {s-b}{2}}\cdot \tan {\frac {s-c}{2}}}}$

hvor s = (a + b + c)/2 er den halve omkretsen til trekanten. Herfra kan man nå beregne dens areal fra S = ER². Når sidene i trekanten blir veldig små, blir den så liten at den går over til å bli tilnærmet plan. I grensen x → 0 kan man benytte at tan x = x slik at uttrykket går over til å bli Herons formel for arealet til en trekant i euklidsk geometri. For at dens grenseovergangen skal være konsistent, må samtidig radius til kulen R → ∞  slik at aR går mot den euklidske sidelengden som også betegnes med a.

Pythagoras for rettvinklet trekant

I euklidsk geometri er Pythagoras' setning den viktigste egenskap for en rettvinklet trekant. Den danner grunnlaget for all trigonometri. En tilsvarende setning gjelder for en rettvinklet, sfærisk trekant. Antar man at den rette vinkelen er γ = 90° med motstående side c, så må de to andre sidene a og b i trekanten da oppfylle ligningen

$\cos c=\cos a\cdot \cos b$

når trekanten befinner seg på en kuleflate. Dette er Pythagoras' setning i sfærisk geometri. Når sidene i trekanten blir veldig korte, kan man approksimere cosinus-funksjonen med cos a = 1 - a²/2 og tilsvarende for de andre faktorene når man ser bort fra ledd av høyere orden. I denne grensen gir da dette resultatet at c² = a² + b² som skyldes at den sfæriske trekanten da er blitt flat og oppfyller euklidsk geometri.

Man kan bevise den sfæriske versjonen av Pythagoras' setning ved å betrakte punktene A, B og C på kuleflaten i et kartesisk koordinatsystem med origo i kulens sentrum O og hvor punktene B og C ligger i xy-planet. Velger man i tillegg at C ligger på y-aksen, vil punktet A være i yz-planet med posisjonsvektor OA = R(0, cos b, sin b). På samme måte har man at punktet B er gitt ved vektoren OB = R(sin a, cos a, 0) da det ligger i xy-planet. Det gir at OA⋅OB = R² cos a⋅cos b. Men da vinkelen mellom vektorene OA og OB er akkurat c, har man også at OA⋅OB = R² cos c. Dermed er cos c = cos a⋅cos b, og Pythagoras' setning er bevist for en rettvinklet trekant. Ved bruk av sfærisk trigonometri kan også siden c i dette tilfellet beregnes direkte fra de to hosliggende vinklene α og β ved bruk av den tilsvarende formelen cos c = cot α⋅cot β.

For en rettsidet trekant, det vil si en sfærisk trekant hvor en av sidene er en rett vinkel, kan man likedan utlede en tilsvarende setning mellom vinklene i trekanten. Er for eksempel siden c = 90°, finner man relasjonen cosγ = - cosα⋅cosβ  for den motsatte vinkelen. Eller den kan uttrykkes ved de to hosliggende sidene a og b som cosγ = - cota⋅cotb.

Polar trekant og dualitet

Den polare trekanten A'B'C' er tegnet i rødt. Den er dual til den gitte trekanten ABC som er tegnet svart.

Hver storsirkel på kuleflaten ligger i et plan som går gjennom kulens sentrum og deler den i to like deler. Normalen til dette planet gjennom sentrum skjærer kuleflaten i to punkter som kalles polene til storsirkelen. Det er helt analogt med at alle punkt langs ekvator på jordkloden ligger like langt fra de to geografiske polene. Dette er i overenstemmelse med den generelle teorien for pol og polare anvendt på sfærisk geometri.

Da sidene i en sfærisk trekant er deler av storsirkler, kan hver side tilordnes to slike poler. For eksempel, for siden BC i figuren defineres nå en bestemt pol A'  ved å velge den som ligger på samme halvdel som punktet A. Dette er nå den duale polen for denne siden. Tilsvarende kan man konstruere de duale polene B'  og C'  for sidene AC og AB. Disse tre nye punktene definerer nå en polar trekant A'B'C'  som er dual til den gitte trekanten ABC.

Ut fra denne konstruksjonen følger også at den duale av trekanten A'B'C'  er den opprinnelige trekanten ABC. Det betyr at punktet A er polen som er dual til siden B'C' . Lengden av sirkelbuene AB'  og AC'  vil derfor begge være π/2 målt i radianer som tilsvarer 90°. Tilsvarende gjelder for de andre hjørnene i trekantene.

Denne dualitet mellom en trekantside og et polpunkt som er hjørne i den polare trekanten, kan uttrykkes matematisk. Det gjøres ved å forlenge siden AB til den skjærer siden B'C'  i den duale trekanten. Skjæringspunktet kan kalles D. På samme måte finnes et skjæringspunkt E når siden AC forlenges og skjærer B'C' . Sirkelbuen DE har dermed lengden |DE | = α da den er en del av storsirkelen gjennom B'  og C'  som har hjørnet A som pol.

Lengden av siden B'C'  i den polare trekanten A'B'C'  kan nå skrives som a'  = B'C'  = B'E  + DC'  - DE . Men nå er C'  polen til AB slik at DC'  = π /2 og likedan B'E  = π /2 da B'  er polen til CA. Dette gir tilsammen a'  = π /2 + π /2 - α = π - α  som er det ønskede resultatet.

Tilsvarende uttrykk kan utledes for de to andre sidene i den polare trekanten. Også dens vinkler kan beregnes og uttrykkes på samme måten ved hjelp av sidene i den opprinnelige trekanten. Samlet finner man da de duale relasjonene

${\begin{alignedat}{3}a'&=\pi -\alpha ,&\qquad b'&=\pi -\beta ,&\qquad c'&=\pi -\gamma ,\\\alpha '&=\pi -a,&\beta '&=\pi -b,&\gamma '&=\pi -c.\end{alignedat}}$

Ved bruk av disse kan man for hver ligning i sfærisk trigonometri finne en dual versjon for den polare trekanten. For eksempel, hvis den gitte trekanten er rettvinklet med γ  = π /2, så gjelder Pythagoras' setning cosc = cosa⋅cosb. Den korresponderende, polare trekanten får da siden c' = π /2  og er derfor rettsidet. Da cos(π - x) = - cos x, transformeres den dermed til den duale utgaven cosγ'  = - cosα' ⋅cosβ'  som nå må gjelde for alle rettsidete, sfæriske trekanter.

Se også

• Sfærisk trigonometri

Litteratur

• I. Todhunter, Spherical Geometry, MacMillan and Co., London (1863). Google Book.
• G. van Brummelen, Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry, Princeton University Press, New Jersey (2013). ISBN 978-0-691-14892-2.