Omhyllingskurve

Omhyllingskurven til en skare med kasteparabler er vist i rødt og er selv del av en parabel som vender nedover.

Omhyllingskurve er en kurve i planet som tangerer hver enkelt kurve i en skare av andre kurver. Den omtales også som en innhyllingskurve eller enveloppe. Man kan definere den som grensen til skjæringspunktene mellom to av de gitte kurvene i skaren når de nærmer seg hverandre.

Evoluten til en kurve i planet er omhyllingskurven til dens normaler.

Definisjonen av en omhyllingskurve kan utvides til også å gjelde i det tredimensjonale rommet til å gi en omhyllingsflate av en skare med andre flater eller kurver.

Innen optikk danner omhyllingsflater av lysstråler brennflater hvor lysintensiteten er spesielt sterk. Lysstrålene er derfor tangenter til en slik brennflate. Et brennpunkt eller fokus til en vanlig linse eller speil er vanligvis en brennflate med svært liten utstrekning.

Beregning

En skare av kurver i planet med kartesiske koordinater (x,y ) kan defineres ved en ligning F(x,y,t ) = 0. For hver verdi av den kontinuerlige parameteren t er dette en implisitt ligning for en kurve y = y(x ). Forandres denne parameteren litt til t + Δt, vil F(x,y,t + Δt ) = 0 beskrive en litt forskjøvet kurve i denne skaren. Ut fra definisjonen av den deriverte funksjon, vil derfor skjæringspunktene mellom de to kurvene oppfylle

$F_{t}(x,y,t)={\partial \over \partial t}F(x,y,t)=0$

Hvis nå t elimineres mellom denne ligningen og den opprinnelige F(x,y,t ) = 0, kommer ligningen for omhyllingskurven y = y(x ) frem. Den har nå sammenfallende tangent med kurven i skaren som den berører.

Eksempel

Et enkelt eksempel er en skare av sirkler med samme radius r = 1, men med et senter som ligger på den rette linjen x = t, y = t. Ligningen for kurveskaren er derfor

$F(x,y,t)=(x-t)^{2}+(y-t)^{2}-1$

Ligningen F_t = 0 gir nå x - t + y - t = 0 slik at t = (x + y )/2. Innsatt i F = 0 gir dette (x - y )² = 2 slik at omhyllingskurven består av de to rette linjene

$y=x\pm {\sqrt {2}}$

parellelle til linjen y = x som sirkelsenterene ligger på. Begge er tangenter til denne skaren. Resultatet er som forventet.

Banene for kast til begge sider med samme hastighet har en omyllingskurve som er en parabel med akse i origo.

Noe mer komplisert er å finne omhyllingeskurven for forskjellige kasteparabler som er kurvene som en ball beskriver når den blir kastet ut fra origo med en viss hastighet v i forskjellige retninger gitt ved en vinkel θ. Langs x-aksen beveger den seg da med konstant hastighet slik at forflytningen i denne retningen er x = vt cosθ hvor nå t er tiden. Samtidig virker tyngdeakselerasjonen g langs den negative y-aksen slik at forflytningen i denne retningen blir

$y=vt\sin \theta -{1 \over 2}gt^{2}$

som følger direkte fra bevegelsesligningen. Eliminerer man tiden t mellom ligningene for disse to bevegelsene, finner man kurven

$y=x\tan \theta -{gx^{2} \over 2v^{2}\cos ^{2}\theta }$

som representerer en skare med parabler med parameter θ. Den kan elimineres ved omhyllingskravet F_θ = 0 som gir tanθ = v²/gx. Dermed blir omhyllingskurven

$y={v^{2} \over 2g}-{gx^{2} \over 2v^{2}}$

Det er igjen en parabel som er symmetrisk om y-aksen.

Linjeskarer

Når ligningen for en rett linje skrives som y = kx + h, kan (k, h ) betraktes som dens linjekoordinater. Hvis disse varierer med en parameter t, vil de fremstille en skare av linjer beskrevet ved nullpunktene til funksjonen

$F(x,y,t)=y-k(t)x-h(t)$

Omhyllingskurven til denne linjeskaren er da gitt ved å eliminere t fra ligningene F = 0 sammen med F_t = 0 som gir k' (t )x + h' (t ) = 0. Her er den t-deriverte av funksjonene er angitt ved et merketegn. Tangentene til denne omhyllingskurven er den opprinnelige linjeskaren.

Eksempel

Astroiden i rødt er omhyllingskurven for en linjeskare med konstant lengde mellom koordinataksene.

En skare med rette linjer kan defineres ved at de to koordinataksene skal skjære av et linjestykke med konstant lengde a. Det tilsvarer linjene som dannes av en stav med denne lengden som settes i et rettvinklet hjørne mellom gulv og vegg. Danner den vinkelen θ med den horisontale x-aksen, har den stigningstallet k = tanθ. Den treffer y-aksen i en høyde h = a sinθ slik at linjeskaren er gitt ved at vinkelen θ varierer i ligningen y = x tanθ + a sinθ.

Omhyllingskurven til denne linjeskaren følger nå fra betingelsen k' (θ )x + h' (θ ) = 0. Den gir løsningen x = - a cos³θ og derfor også y = a sin³θ som bedriver kurven uttrykt ved parameteren θ. Elimineres denne, finnes den eksplisitte formen

$x^{2/3}+y^{2/3}=a^{2/3}$

som viser at kurven er en astroide eller stjernekurve. Dette er en spesiell hyposykloide.

Dürers konkoide

Tegning av Albrecht Dürer som viser konstruksjon av hans konkoide som er kurven til venstre. Omhyllingskurven til høyre er en del av en parabel.

I et verk fra nesten 500 år siden viste Albrecht Dürer hvordan man med et stykke tråd av en gitt lengde kan konstruere en spesiell kurve som senere er blitt kalt for Dürers konkoide. Har tråden en lengde a, fester man den ene enden i punktet x = a på x-aksen og strekkes mot origo. Så flyttes dette endepunktet til x = a - t samtidig som den strekkes gjennom punktet y = t på y-aksen. Gjøres dette flere ganger for jevnt fordelt verdier av parameteren t, vil det andre endepunktet av tråden beskrive en kurve som siden har fått Dürers navn.

For hver verdi av parameteren t, vil tråden danne et stykke av den rette linjen med ligningen

$y={t \over t-a}x+t$

Denne linjeskaren har nå en omhyllingskurve som igjen kan finnes fra betingelsen k' (t )x + h' (t ) = 0 som her gir

$ax=(a-t)^{2}$

Dermed kan parameteren t  uttrykkes ved koordinaten x og benyttes i skareligningen. Det gir

${\begin{aligned}y&=x+{ax \over t-a}+t=x-{ax \over {\sqrt {ax}}}+a-{\sqrt {ax}}\\&=({\sqrt {a}}-{\sqrt {x}})^{2}\end{aligned}}$

Omhyllingskurven er derfor en del av den konkave superellipsen

$x^{1/2}+y^{1/2}=a^{1/2}$

Ved å kvadrere ligningen, finner man den alternative formen

$(x-y)^{2}+a^{2}=2a(x+y)$

Den variable x + y øker derfor kvadratisk med x - y slik at kurven er en parabel med akse langs linjen y = x.

Evoluter

Evoluten til en ellipse dannes av omhyllingskurven til dens normaler og er en konkav superellipse.

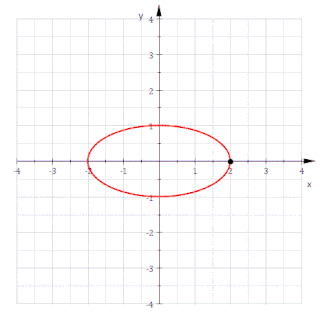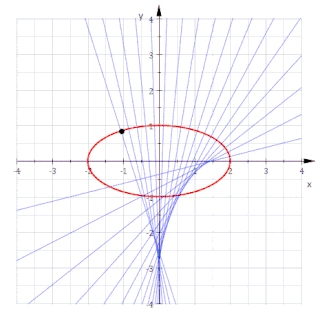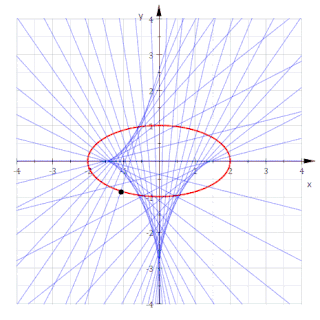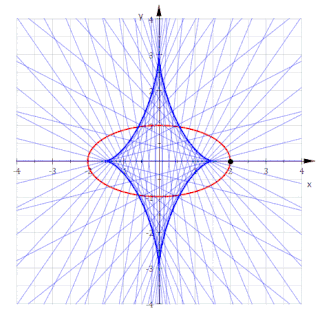
Krumningssentrene til en plan kurve danner en ny kurve som kalles den evolute. Den er samtidig omhyllingskurven til alle normalene til den opprinnelige kurven.

Hvis man betrakter en vanlig ellipse med to hovedakser a og b, er den vanligvis beskrevet ved ligningen

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$,

Alternativt kan dette uttrykkes på parameterform som r(t ) = (x(t ), y(t )) hvor x(t ) = a cost og y(t ) = b sint. Tangenten til ellipsen er dermed t = d r/dt = (-a sint, b cost ). Normalen n står vinkelrett på denne slik at den er n = (b cost, a sint ) hvis den velges å være rettet utover fra ellipsens sentrum. Den definerer nå en linje med stigningstall

$k(t)={a \over b}\tan t$

og beskrevet ved ligningen y = kx + h. Skjæringspunktet h = h(t ) med y-aksen bestemmes ut fra kravet at ellipsepunktet (x(t ), y(t )) også må ligge på linjen. Det gir

$h(t)={b^{2}-a^{2} \over b}\sin t$

Omhyllingskurven til disse normalene følger igjen fra betingelsen k' x + h'  = 0. Den gir dens form på parameterfremstillingen

$x={c^{2} \over a}\cos ^{3}t,\;\;\;y=-{c^{2} \over b}\sin ^{3}t$

hvor c² = a² - b² er den kvadrerte avstand til ellipsens brennpunkt. På implisitt form har denne evoluten ligningen

$(ax)^{2/3}+(by)^{2/3}=c^{4/3}$

Den er derfor en konkav superellipse med eksponent 2/3 som også kalles en subellipse eller asymmetrisk astroide.

Omhyllingsflater

En flate i det tredimensjonale rommet kan angis på implisitt vis ved en ligning F(x,y,z ) = 0. Hvis ligningen i tillegg avhenger av en kontinuerlig parameter t, vil ligningen F(x,t ) = 0 fremstille en skare av flater der x = (x,y,z ) angir punkt på disse flatene. På samme måte som for omhyllingskurver i planet, vil nå en omhyllingsflate av denne skaren med flater i tillegg oppfylle at den deriverte F_t (x,t ) = 0.

Kanalflater

Skaren med kuler til venstre er omhyllet av en kanalflate til høyre.

Når skaren av flater er kuler med radius r = r(t ) hvis senter ligger på en glatt kurve c = c(t ) som kalles senterkurven, kalles omhyllingsflaten for en kanalflate. Den er gitt ved ligningen

$F(\mathbf {x} ,t)={\big (}\mathbf {x} -\mathbf {c} (t){\big )}^{2}-r^{2}(t)=0$

I det spesielle tilfellet at radius er konstant, vil denne bli en rørflate. Et kjent eksempel er en torus der senterkurven er en sirkel.

Et enkelt eksempel er en skare med kuler som har sitt senter liggende på z-aksen i avstand at fra origo der t = 0. Hvis også deres radius varier proporsjonalt med t slik at r(t ) = bt der b < a, er kuleskaren gitt ved

$F(x,y,z,t)=x^{2}+y^{2}+(z-at)^{2}-(bt)^{2}$

Fra betingelsen F_t = 0 følger at az = (a² - b²)t som innsatt i F = 0 gir omhyllingsflaten

$x^{2}+y^{2}={z^{2}b^{2} \over a^{2}-b^{2}}$

Dette beskriver en kjegle med akse langs z-aksen. Snittflaten med plan parallelt med xy-planet er sirkler hvis radius øker proporsjonalt med z.

Dupin-syklider

Typisk Dupin-syklide med nett av krumningslinjer som alle er sirkler.

Det finnes spesielle kanalflater som kan tilordnes til to forskjellige senterlinjer. De kalles for Dupin-syklider. Et trivielt eksempel er en torus. Den ene senterlinjen er da tydelig, mens den andre er mer skjult. Spesielt for denne flaten er at den kan dekkes av et nett med sirkler som skjærer hverandre vinkelrett. De er linjer gjennom punkt med samme krumning. Dette karakteriserer en generell syklide.

Da en rett linje kan betraktes som en del av en sirkel med uendelig stor radius, er derfor en rett sylinder eller kjegle også trivielle eksempel på slike flater.

Opprinnelig ble disse flatene funnet som omhyllingsflater for en skare av kuler som skal plasseres slik at de tangerer tre gitte kuler med vilkårlige radier. De tre tangentpunktene kan være innvendige eller utvendige.

Noe senere ble det vist at Dupins generelle syklider kan finnes ved inversjon i en fritt valgt kule av de trivielle syklidene representert ved torusen, sylinderen og kjeglen. Under denne transformasjonen bevares vinkler mellom skjærende linjer slik at de resulterende krumningslinjene er sirkler som forblir ortogonale til hverandre. Avhengig av hvordan posisjonen til kulen er relativ til flaten som skal inverteres, fremkommer syklider i forskjellige former.