Evolute

Evoluten til en ellipse i rødt er subellipsen i blått.

Evoluten til en kurve er omhyllingskurven til dens normaler. Den kan også defineres som det geometriske sted for krumningssentrene til kurven. Disse definisjonene kan også benyttes til å definere evoluten til en flate. I optikken er dette brennflaten eller kaustikken til den gitte flaten.

Nær forbundet med evoluten er evolventene til kurven. Den gitte kurven er evoluten til hver av dens evolventer.

Egenskapen til både evoluter og evolventer ble først undersøkt av den nederlandske videnskapsmann Christiaan Huygens på midten av 1600-tallet i forbindelse med hans arbeider med å konstruere mer nøyaktige klokker.

Definisjon

En kurve i det todimensjonale planet kan angis som en funksjon r(s) når man benytter naturlig parametrisering der s er dens buelengde. For at et punkt x skal være på evoluten, må det finnes et punkt r(s) på kurven slik at vektoren x - r(s) ligger på en linje som har samme retning som kurvenormalen n i dette punktet. Det betyr at retningen til linjen må oppfylle betingelsen

$F(\mathbf {x} ,s)=(\mathbf {x} -\mathbf {r} (s))\cdot \mathbf {t} =0$

der t = d r/ds er tangentvektoren til den gitte kurven med t⋅n = 0 og t⋅t = 1. Hele evoluten er nå gitt som omhyllingskurven til disse linjene og må oppfylle kravet

$F_{s}(\mathbf {x} ,s)={\partial \over \partial s}F(\mathbf {x} ,s)=0$

Ved å utføre denne derivasjonen, finner man at

${\begin{aligned}F_{s}(\mathbf {x} ,s)&=(\mathbf {x} -\mathbf {r} )\cdot {d\mathbf {t} \over ds}-{d\mathbf {r} \over ds}\cdot \mathbf {t} \\&=\kappa (\mathbf {x} -\mathbf {r} )\cdot \mathbf {n} -1\end{aligned}}$

når man benytter Frenets formel d t/ds = κ n der κ er kurvens krumning. Betingelsen F_s(x,s) = 0 gir dermed resultatet

$\mathbf {x} =\mathbf {r} +\rho \,\mathbf {n}$

hvor ρ = 1/κ er krumningsradius til kurven i det punktet hvor normalen n har sitt fotpunkt. Evoluten faller derfor sammen med det geometriske sted for kurvens krumningssenter.

Dette kan benyttes for det tilfelle at den gitte kurven har en vilkårlig parametrisering r = (x(t ), y(t )). Koordinatene til krumningssenteret er da

${\begin{aligned}x_{c}&=x-{x'^{2}+y'^{2} \over x'y''-x''y'}y'\\y_{c}&=y+{x'^{2}+y'^{2} \over x'y''-x''y'}x'\end{aligned}}$

som også vil være ligningen for kurvens evolute.

Tangenter

Da evoluten til en kurve er gitt som omhyllingskurven til dens normaler, vil disse være tangenter til evoluten. Da denne er gitt ved ligningen x = x(s) når man parametrisere den med den opprinnelige kurvens buelengde s, er tangentene gitt ved

$\mathbf {T} ={d\mathbf {x} \over ds}=\mathbf {x'}$

når man indikerer en derivasjon med hensyn til buelengden s med et merke. Nå er x = r + ρ n slik at

$\mathbf {T} =\mathbf {r'} +\rho '\mathbf {n} +\rho \mathbf {n'}$

Her er r'  = t  som sammen med Frenets andre formel n'  = -κ t gir at T = ρ' n. Det bekrefter at evolutens tangent T er langs normalen n til den gitte kurven. Men resultatet viser også at der krumningen til denne kurven har en ekstremalverdi hvor den deriverte ρ'  = 0, er tangenten ikke veldefinert. Evoluten har derfor i dette punktet en spiss eller annen singularitet.

Eksempel

Evoluten (rød) til en ellipse (blå). Til høyre er inntegnet en krumningssirkel.

En ellipse med hovedakser a og b er på parameterform gitt ved x(t ) = a cost og y(t ) = b sint. Den har maksimal krumning i punktene (±a,0) og minimal krumning i punktene (0,±b). Dens evolute forventes derfor å ha spisser i disse fire retningene.

Fra uttrykket for krumningssenteret finner man koordinatene til evoluten som

${\begin{aligned}x_{c}&=x-{a^{4}y^{2}+b^{4}x^{2} \over a^{4}b^{2}}x={a^{2}-b^{2} \over a^{4}}x^{3}\\y_{c}&=y+{a^{4}y^{2}+b^{4}x^{2} \over a^{2}b^{4}}y={b^{2}-a^{2} \over b^{4}}y^{3}\end{aligned}}$

når man benytter ligningen a²y² + b²x² = a²b² for ellipsen. Ved å innføre den kvadrerte avstanden c² = a² - b² til brennpunktet, er krumningssenteret til punktet (x, y ) gitt ved

$x_{c}={c^{2} \over a}\cos ^{3}t,\;\;\;y_{c}=-{c^{2} \over b}\sin ^{3}t$

En sirkelevolvent som starter i punktet A. Omhyllingskurven til dens normaler er den samme sirkelen.

Det ligger derfor på kurven gitt på den implisitte formen

$(ax)^{2/3}+(by)^{2/3}=c^{4/3}$

og utgjør ellipsens evolute. Den er en subellipse med samme form som en asymmetrisk astroide.. I det spesielle tilfellet at a = b slik at c = 0, vil ellipsen bli en sirkel og evoluten reduseres til et enkelt punkt (0, 0) som er sirkelens sentrum.

Evoluten til andre, kjente kurver kan beregnes på tilsvarende måte. For eksempel er evoluten til traktrisen en kjedelinje.

Det er naturlig å undersøke om det finnes en kurve som har en sirkel til evolute. Denne kurven må da være en evolvent til sirkelen r(t) = (cos t, sin t ) og kalles derfor for sirkelevolventen. Den har parameterfremstillingen

$x(t)=\cos t+t\sin t$

$y(t)=\sin t-t\cos t$

når evolventen starter i punktet t = 0 på sirkelen. Den er en slags spiral som snor seg om sirkelen med stadig større radius.

Brennflater

Kaustikken som dannes av parallelle lysstråler som reflekteres i et sirkulært speil, er en nefroide.

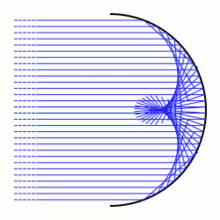
Et brennpunkt eller fokus til en vanlig linse eller speil i optikken er vanligvis en brennflate eller kaustikk med svært liten utstrekning. Generelt kan en brennflate defineres som omhyllingsflaten til lysstrålene som antas å være rette linjer. Da disse står vinkelrett på bølgefronten eller eikonalen, kan derfor brennflaten identifiseres med evoluten til bølgefronten. Lysstrålene er derfor dens tangenter.

Når lysstrålene er symmetriske om en akse, vil bølgefronten og dermed også brennflaten være rotasjonssymmetrisk om denne aksen. Et plant snitt langs aksen vil da skjære flaten langs en kurve som er den tilsvarende brennkurven. Den bestemmer derfor hele brennflaten i dette symmetriske tilfellet. Ordet brennkurve blir også benyttet mer generelt for andre snitt av brennflaten som når den observeres på en plan flate eller skjerm.

En brennflate som oppstår ved refleksjon av lysstråler kalles en katakaustikk, mens en diakaustikk kan fremkomme ved refraksjon. I det første tilfellet er den lettest å beregne ved å første finne den sekundære kaustikken. Den avhenger av lokaliseringen til lyskilden samt formen til det reflekterende speilet. Den resulterende katakaustikken er da evoluten til denne sekundære kaustikken.

Et av de mest kjente eksempel er katakaustikken som kan oppstå i en kopp med te eller kaffe. Koppen fungerer da tilnærmet som et sirkulært hulspeil som skaper en lysende brennkurve i væskeoverflaten. Denne kurven er halvparten av en nefroide som er en spesiell episykloide.

Eksterne lenker

• «Evolute of an Ellipse», video fra youtube