Polygon

En polygon eller mangekant er i geometri en plan lukket kurve, sammensatt av et endelig antall rette linjesegment. Også figuren eller området innenfor kurva omtales som en polygon. En trekant og en firkant er begge eksempler på polygoner. Noen polygoner har fått egne navn, som pentagrammet. Dette er eksempel på en regulær mangekant.
Linjesegmentene i en polygon møtes i et hjørne, og vanligvis krever en at vinkelen mellom to møtende linjesegment er ulik 180 grader. Linjesegmentene kalles sidekanter eller kanter i polygonen. En linje som går mellom to punkter i mangekanten, men som ikke er en del av mangekanten, kalles en diagonal.
En enkel polygon er en polygon der sidekantene ikke skjærer hverandre. Ofte defineres en polygon til å være ensbetydende med «enkel polygon».[1] I en enkel polygon er antall hjørner lik antall sidekanter. Polygoner kan klassifiseres etter antall sidekanter.
I analytisk geometri kan en definere en polygon ved å gi koordinatene til alle hjørnene.
Ordet «polygon» har opphav i det greske πολύς (polús) «mange» og γωνία (gōnía) «vinkel».[2] Istedenfor å uttrykke at figuren har mange kanter, så sier «polygon» at figuren har mange vinkler eller hjørner. Da antall kanter er likt med antall hjørner, er en n-gon det samme som en n-kant. Derfor brukes for eksempel ofte betegnelsene femkant og pentagon om hverandre hvor penta kommer fra det greske ordet for fem. Av samme grunn kunne derfor også en trekant bli kalt for en trigon. Dette har overlevd i ordet trigonometri. Likedan ville en firkant kunne kalles en tetragon.
En digon er en polygon med to hjørner og er derfor en tokant. I euklidsk geometri består den av to sammenfallende linjestykker og er derfor uinteressant. Det er den derimot ikke i sfærisk geometri hvor den vanligvis omtales som en sfærisk tokant.
For polygoner med n = 3 og 4 benyttes også navn med latinsk opphav. En trekant omtales da som et triangel, mens en firkant kan kalles et kvadrangel hvor angel-endelsen refererer til antall hjørner.
Klassifikasjon etter antall kanter[rediger | rediger kilde]
En polygon kan karakteriseres som en trekant, firkant, femkant og så videre, eller generelt som en n-kant. Også greske navn er i bruk, som vist i den følgende tabellen.
| Navn | Sidekanter | Merknad |
|---|---|---|
| Henagon (eller monogon) | 1 | Umulig i euklidsk geometri og derfor ikke alltid betraktet som ekte polygon. |
| Tokant (eller digon) | 2 | Degenerer i euklidsk geometri til et linjestykke. |
| Trekant (eller trigon) | 3 | Den enkleste polygonen i euklidsk geometri. |
| Firkant (eller tetragon) | 4 | Den enkleste polygonen som kan være konkav. |
| Pentagon | 5 | En stjerneformet pentagon er kjent under navnet pentagram. |
| Heksagon | 6 | |
| Heptagon | 7 | |
| Oktogon | 8 | |
| Enneagon (eller nonagon) | 9 | «Nonagon» er vanlig, men blander latinsk novem = 9 med gresk. Formen «enneagon» er ren gresk. |
| Dekagon | 10 | |
| Hendekagon | 11 | |
| Dodekagon | 12 | |
| Tridekagon (eller triskaidekagon) | 13 | |
| Tetradekagon (eller tetrakaidekagon) | 14 | |
| Pentadekagon (eller quindekagon eller pentakaidekagon) | 15 | |
| Heksadekagon (eller heksakaidekagon) | 16 | |
| Heptadekagon (eller heptakaidekagon) | 17 | |
| Oktadekagon (eller octakaidekagon) | 18 | |
| Enneadekagon (eller enneakaidekagon eller nonadekagon) | 19 | |
| Ikosagon | 20 | |
| Triakontagon | 30 |
Andre typer klassifikasjon[rediger | rediger kilde]
En polygon er konveks dersom en vilkårlig rett linje gjennom polygonen skjærer sidekantene i kun to punkt. Dette er ekvivalent med at alle vinklene mellom sidekantene er mindre enn 180 grader. En polygon som ikke er konveks er ikke-konveks.
En enkelt polygon er en polygon der ingen av sidekantene skjærer hverandre. En konveks polygon er alltid enkelt.
En konkav polygon er en enkel polygon som ikke er konveks.
En polygon er syklisk dersom alle hjørnene ligger på en felles sirkel. I en likesidet polygon er alle sidekantene like lange. En regulær polygon er en likesidet, syklisk polygon.
Diagonaler[rediger | rediger kilde]

En diagonal i en polygon er en linje som forbinder et hjørne med et annet, ikke-nærliggende hjørne. Fra hvert hjørne i en polygon med n hjørner kan det derfor gå ut n - 3 diagonaler. Det totale antall diagonaler nd er derfor
da man må dele på to for å unngå å telle samme diagonal dobbelt opp. For eksempel, for en enkel 12-kant er antallet diagonaler 12⋅(12 - 3)/2 = 108/2 = 54.
Antall måter et konvekst polygon med n + 2 kanter kan deles opp i n trekanter ved hjelp av ikke-kryssende diagonaler er gitt ved Catalan-tallet Cn.[3]
Vinkler[rediger | rediger kilde]
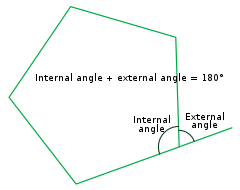
I hvert hjørne møtes to sidekanter. De skjærer hverandre under en vinkel som på innsiden av polygonen kalles den indre vinkelen βi. Den supplementære vinkelen γi = 180° - βi kalles den ytre vinkelen. I polygoner som ikke er konvekse, kan noen av de indre vinklene være større en 180°.
Man kan beregne summen av de indre vinklene i en n-kant ved å dele den opp i trekanter. Ved å trekke alle n - 3 diagonalene fra et hjørne, deles den opp i n - 2 trekanter. Da summen av de indre vinklene for hver av dem er 180°, betyr det at
- .

I en firkant er derfor summen av de indre vinklene like 360°. I en regulær mangekant er alle indre vinkler like store og lik med (1 - 2/n)⋅180°. De indre vinklene i en likesidet trekant er derfor alle lik med 60°. Når antall sidekanter n derimot blir veldig stort, vil den indre vinkelen i en regulær mangekant nærme seg 180°.
Mens summen av indre vinkler i en polygon øker med antall sider, er summen av de ytre vinklene i en vilkårlig,enkel polygon konstant og lik med 360°. Det følger direkte fra definisjonen,
- .
Dette resultatet kan geometrisk forstås ved at summen representerer alle dreiningene av sidekantene i polygonen når man går fra et hjørne og rundt den tilbake til samme punkt. Summen er derfor en fullstendig rotasjon, det vil si 360°. Dette gjelder både for konvekse og ikke-konvekse polygoner. I en regulær mangekant er derfor hver ytre vinkel lik med 360°/n.
Areal[rediger | rediger kilde]

Arealet A av en enkel n-kant kan beregnes ved å dele den opp i trekanter og summere arealene til hver av dem. Hvis en slik trekant er gitt ved hjørnene P1 = (x1,y1), P2 = (x2,y2), og P3 = (x3,y3), så følger arealet av trekanten fra formelen
Er punktene ordnet mot klokkeretningen, blir arealet positivt.
En firkant definert ved hjørnene P1, P2, P3 og P4 kan nå betraktes som bestående av trekantene P1P2P3 og P1P3P4. Tilsammen har disse to trekantene arealet
Man ser at bidragene fra den felles siden P1P3 i de to trekantene har falt bort.
Dette gjør det nå mulig å finne formelen for arealet til en vilkårlig n-kant ved å betrakte den som sammensatt av en polygon med n - 1 sider pluss en trekant med hjørne Pn og en delt side P1Pn-1. Den kan skrives som
hvor xn+1 = x1 og yn+1 = y1. Igjen kansellerer bidraget fra siden P1Pn-1 ut i summen. Den opprinnelige utledningen av formelen går tilbake til den tyske matematiker Carl Friedrich Gauss.
Som et eksempel kan man betrakte femkanten gitt ved hjørnene (3,4), (5,11), (12,8), (9,5), and (5,6). Den er enkel da ingen sider skjærer hverandre, men den er ikke konveks. Den har arealet A = (1/2)×(3⋅11 - 4⋅5 + 5⋅8 - 11⋅12 + 12⋅5 - 8⋅9 + 9⋅6 - 5⋅5 + 5⋅4 - 6⋅4) = 60/2 = 30.
Tyngdepunkt[rediger | rediger kilde]
I en enkel polygon er koordinatene til tyngdepunktet gitt ved formelen
Referanser[rediger | rediger kilde]
- ^ E.J.Borowski, J.M.Borwein (1989). Dictionary of mathematics. Glasgow: Collins. s. 457. ISBN 0-00-434347-6. [Polygon]
- ^ Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. s. 167. ISBN 0-88385-511-9.
- ^ følge A000108 i OEIS








