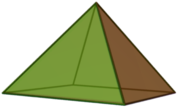
Kvadratisk pyramide

Type		Johnson-legeme J92 – J1 – J2
Dualt polyeder		Seg selv
Størrelser
Sider		5 4 trekanter 1 kvadrat
Kanter		8
Hjørner		5

En kvadratisk pyramide brettet ut over en todimensjonal flate.

En kvadratisk pyramide er en pyramide med en kvadratsik grunnflate. Hvis toppunktet er vinkelrett over kvadratets sentrum, vil den ha symmetrien C_4v.

Johnson-legeme (J1)

Hvis alle sidene er likesidede trekanter, er pyramiden et Johnson-legeme (J₁). De 92 Johnson-legemene ble fikk navn og ble beskrevet av den canadiske matematikeren Norman Johnson i 1966.

Denne kvadratiske Johnson-pyramiden kan karakteriseres ut ifra én enkelt kantlengde av parameter a. Høyden h (fra kvadratets midtpunkt til toppunktet), er en slik pyramides areal A (med alle fem sidene) og volum V følgende:

$h={\frac {1}{\sqrt {2}}}a$

$A=(1+{\sqrt {3}})a^{2}$

$V={\frac {\sqrt {2}}{6}}a^{3}.$

Andre kvadratiske pyramider

Andre kvadratiske pyramider har likebeinte trekanter som sider.

For kvadratpyramider generelt, med grunnkantlengde l og høyde h, er arealet og volumet:

$A=l^{2}+l{\sqrt {l^{2}+(2h)^{2}}}$

$V={\frac {1}{3}}l^{2}h.$

Nære polyedre

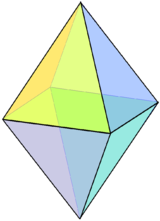
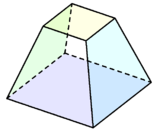
Et regulært oktaeder kan bli sett på som en firkantet bipyramide, dvs. to kvadratisk Johnson-pyramider satt sammen bunn mot bunn.	Tetrakisheksaederet kan bli konstruert fra en kube med en kort kvadratpyramide lagt på hver side.	Et kvadratisk avstumpet pyramide er en kvadratpyramide med toppunktet kuttet av.

Dualt polyeder

Den kvadratiske pyramiden er topologisk sett et selvdualt polyeder. Dualens kantlengde er ulik på grunn av polar gjenngjeldelse.

Dual til kvadratisk pyramide	Dual sin flate

Topologi

Som alle pyramider er den kvadratiske pyramider selvdual, da de har like mange sider som hjørner.

Kvadratpyramiden kan representeres med Wheel-fremstillinga W₅.

Eksterne lenker

• Eric W. Weisstein, Square pyramid(Johnson solid) hos MathWorld
• Eric W. Weisstein, Wheel graph
• Square Pyramid -- Interaktiv polyedermodell
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra (VRML model)