Harmonisk oscillator

En harmonisk oscillator er i fysikken et svingende system der den tilbakeførende kraften er proporsjonal med avviket fra systemets likevektsposisjon.
Kjente eksempel er et svingende lodd hengende i en fjær eller en pendel som går frem og tilbake. Svingningen sies å være harmonisk når den er beskrevet ved en sinuskurve med en konstant periode. En slik ideell bevegelse spiller en meget viktig rolle i klassisk mekanikk, elektriske kretser og i kvantemekanikken.
Selv om perioden til bevegelsen er konstant, behøver ikke bevegelsen være harmonisk. For eksempel vil en pendel med et stort utsving, ha en bevegelse som ikke er beskrevet ved en sinus-funksjon, men derimot ved en elliptisk funksjon. Dette kalles vanligvis for en matematisk pendel og er et eksempel på en «ikke-harmonisk» oscillator. Bevegelsen vil være uharmonisk.
I mange tilfeller vil perioden til oscillasjonen ikke være konstant, men derimot øke med tiden. For et mekanisk system vil dette skyldes friksjon eller luftmotstand. Oscillatoren sies da å være «dempet». Den kan også være påvirket av ytre krefter og er da «drevet». Hvis den ytre kraften varierer i takt med svingningen til oscillatoren, kan man få resonans.
Den harmoniske bevegelsen kan skje i mer enn en dimensjon. En pendel kan for eksempel bevege seg langs en kjegle i stedet for i et plan. Den kalles da for en todimensjonal harmonisk oscillator. I fysikken finnes det mange eksempel på tredimensjonale oscillatorer som mange ganger også kan være koblet sammen med hverandre.
I kvantemekanikken spiller den harmoniske oscillator en overraskende viktig rolle. Det skyldes først og fremst at den representerer et av meget få mekaniske system hvis bevegelse kan eksakt beregnes kvantemekanisk på en enkel måte. Denne kan derfor benyttes som utgangspunkt til å gi tilnærmede beskrivelser av andre kvantesystem som ikke har eksakte løsninger. Men denne oscillatoren er også selve grunnelementet for all kvantefeltteori da alle frie kvantefelt kan beskrives som bestående av en uendelig sum av slike sammenkoblede, tredimensjonale harmoniske oscillatorer. Kjennskap til én kvantisert harmonisk oscillator gjør det da mulig å beregne alle egenskaper til kvantefeltet.
Anvendelser[rediger | rediger kilde]
Den harmoniske oscillatoren er et viktig eksempel i fysikkundervisning siden likningene er forholdsvis lett håndterlige og gir en forståelse for oscillasjoner som kan relateres til hverdagslige fenomener.
Spenningen i det norske strømnettet er ett eksempel på en størrelse som oscillerer harmonisk. Amplituden er på cirka 320 volt (med en effektivverdi av 230 volt), og frekvensen er 50 Hz. Gamle pendelur gjør seg bruk av det faktum at svingeperioden til pendelen er essensielt uavhengig av utslaget, så lenge utslaget er lite. Dette gjør at en klokke-eier slipper å tenke på hvor mye hen trekker pendelen ut til sida.
Matematisk beskrivelse[rediger | rediger kilde]

La oss tenke oss en partikkel eller gjenstand med masse m som kan bevege seg uten friksjon i en retning under påvirkning av en kraft F. Denne kan for eksempel skyldes en fjær. Strekkes denne et stykke x fra sin likevektsposisjon, vil den prøve å trekke massen tilbake til denne. I det enkleste tilfellet er kraften i fjæren beskrevet ved Hookes lov som sier at F = - kx hvor k er fjærkonstanten. Minustegnet tilsvarer at kraften virker i retning mot likevektsposisjonen.[1] Bevegelsen til massen er gitt ved Newtons andre lov som her betyr at
Dette er en differensialligning av andre orden. Løsningen vil derfor i alminnelighet inneholde to konstanter som må bestemmes ut fra grensebetingelser. Ofte velges de å være posisjon og hastighet ved et gitt tidspunkt og kan uttrykkes ved en amplitude A og fasefaktor φ. Dermed kan den generelle løsningen skrives på formen
Settes dette inn i differensialligningen, finner man at
som er vinkelfrekvensen. Den gir også perioden T = 1/f til den sinusformete bevegelsen hvor den vanlige frekvensen f = ω/2π. Oscillatoren svinger desto raskere når massen blir mindre og fjærkonstanten større.
Fasefaktoren forteller i hvilken posisjon den starter i og amplituden er maksimalt utslag. For en fjær som trekkes og slippes ved tiden t = 0, er φ = 0 og A er posisjonen den slippes fra. Hvis grensebetingelsene i stedet er at den starter i posisjon x = 0 ved tiden t = 0, men med en hastighet dx/dt = v, ville φ = π /2 og amplituden A = v/ω.
Energier[rediger | rediger kilde]
Den kinetiske energien til oscillatoren er
når man skriver hastigheten som . Tilsvarende er den potensielle energien
Dermed er den totale, mekaniske energien
er konstant. Den avhenger av amplituden A og fjærkonstanten k, men er uavhengig av massen til den oscillerende partikkelen. Under sin bevegelse svinger energien fra å være ren stillingsenergi i de to ytterpunktene og ren bevegelsesenergi i midtpunktet mellom disse.
Løsning av bevegelsesligning[rediger | rediger kilde]
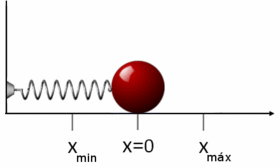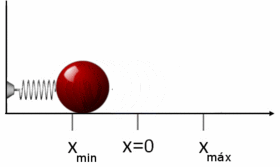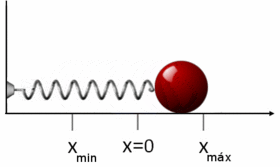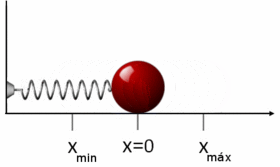
Differensialligningen som beskriver bevegelsen til oscillatoren, kan skrives som
Den vil i alminnelighet ha flere løsninger. Hvis x1(t ) er en løsning og x2(t ) er en annen løsning, så vil også summen (eller «superposisjonen») a x1(t ) + b x2(t ) være en løsning hvor a og b er vilkårlige konstanter. Ligningen sies derfor å være lineær med x1(t ) og x2(t ) som delløsninger.
Slike delløsninger av en lineær differensialligning finnes på enkleste måte ved å anta at de kan skrives som en eksponensialfunksjon.[2] Da er x(t ) = exp(αt) hvor foreløbig størrelsen α er ukjent. Settes denne antagelsen inn i ligningen, finner man
Denne er kun oppfylt når α = ±iω hvor i = √-1 er den imaginære enhet. Derfor er den generelle løsningen av differensialligningen
Da koordinaten x er et reelt tall, må de to integrasjonskonstantene a og b være komplekskonjugerte av hverandre. Ved å benytte Eulers formel for eksponensialfunksjonene, kan løsningen skrives på formen
etter å ha erstattet de to opprinnelige integrasjonskonstantene med to andre, reelle konstanter B og C. Alternativt kan nå dette skrives på den opprinnelige formen x = A cos(ωt - φ) når man innfører B = A cosφ og C = A sinφ og gjør bruk av den trigonometriske identiteten for cosinus til en differanse av to vinkler. Maksimalt og minimalt utslag er henholdsvis xmax = A og xmin = -A.
Andre utledninger[rediger | rediger kilde]
Differensialligningen som beskriver bevegelsen til oscillatoren, kan finnes på andre måter som ved bruk av Lagrange-mekanikk eller Hamilton-mekanikk.[3] Men den enkleste måten tar utgangspunkt i at den totale energien
er konstant. Den deriverte med hensyn på tiden er derfor null slik at
hvor er den dobbeltderiverte av x. For at denne ligningen skal være oppfylt, må enten eller at innholdet i parentesen er null. Det første alternativet er uinteressant da den betyr at partikkelen har null hastighet og derfor ligger i ro. Men den andre betingelsen betyr at ligningen
må være oppfylt. Den er den samme som tidligere funnet og kalles vanligvis for svingeligningen for vinkelfrekvens ω. Det er den fundamentale bevegelsesligningen for den harmoniske oscillator.
Dempet oscillator[rediger | rediger kilde]
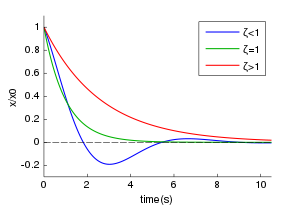
I praksis vil en harmonisk oscillator være utsatt for friksjon. Denne vil bevirke at hastigheten blir redusert eller «dempet» slik at utslagene blir mindre og mindre og til slutt dør helt ut. Ofte kan denne friksjonskraften antas å være proporsjonal med hastigheten. Dermed blir bevegelsesligningen for oscillatoren forandret til
hvor b er friksjonskonstanten. Friksjonskraften er ikke konservativ, og en dempet oscillator i bevegelse vil alltid ende opp i ro ved at dens energi E er gått over i friksjonsvarme. Det følger fra
hvor leddet på høyre side alltid er negativt. Energien avtar derfor med tiden uansett hvordan oscillatoren beveger seg.[4]
Skriver man den som b = 2mγ, tar ligningen for den dempete oscillatoren standardformen
hvor nå ω0 = √(k/m) er vinkelfrekvensen for den udempete svingningen. Det er fremdeles en differensialligning av andre orden slik den generelle løsningen vil igjen involvere to integrasjonskonstanter.
Den nye bevegelsesligningen er lineær og kan igjen løses ved antagelsen x(t ) = exp(αt). Da må den ukjente størrelsen α oppfylle
Denne andregradsligningen har i alminnelighet to løsninger som er
De fysiske egenskapene til løsningene avhenger av hvor stor friksjonskoeffisienten γ er i forhold til egenfrekvensen ω0. Man finner dermed tre kategorier av dempete svingninger.
Overdempning[rediger | rediger kilde]
Når γ > ω0 er begge verdiene for α negative. Den generelle løsningen for bevegelsen er da
hvor igjen A og B er konstanter og
Hvis oscillatoren starter med null hastighet, beveger den seg langsomt tilbake mot likevektspunktet som den først når etter uendelig lang tid.
Kritisk dempning[rediger | rediger kilde]
I det meget spesielle tilfellet at γ = ω0 faller de to løsningene for α sammen. Dempningen er da «kritisk». Det kan da se ut til at det bare er en løsning med α = - γ. Men det vises lett at nå er også t exp(αt) en løsning. Derfor er den generelle løsningen i dette kritiske tilfellet
Igjen er det ingen oscillasjoner i bevegelsen. Men hvis den starter med null hastighet, kan den i dette tilfellet bevege seg litt forbi likevektspunktet x = 0 før utslaget langsomt går mot null. Dette avhenger av det relative forholdet mellom konstantene A og B.
Underdempning[rediger | rediger kilde]

Når dempningen er svak, vil γ < ω0 og begge løsningene for α er komplekse tall. Skrives disse som
- ,
kan den generelle løsningen i dette tilfellet med «underdempning» skrives som
Dette er en harmonisk svingning med en litt redusert frekvens
og en amplitude som blir mindre med tiden på grunn av den eksponentielle dempningsfaktoren i løsningen.
Hvis man betrakter det generelle tilfellet at oscillatoren starter i posisjon x0 med hastighet v0, kan de to konstantene A og B bestemmes. Da blir løsningen
Hvis dempningen nå øker slik at γ → ω0, vil frekvensen Ω → 0. Benytter man da at i denne grensen vil sin Ωt /Ω → t, finner man derved den generelle løsningen for kritisk dempning.
Tvungen svingning[rediger | rediger kilde]
Av stor praktisk og teoretisk betydning er forståelsen av hvordan en dempet oscillator beveger seg når den er påvirket av en ytre kraft F(t ) som varierer med tiden. Oscillatoren sies da å være «drevet» og vil utføre en tvungen svingning beskrevet ved bevegelsesligningen
Den er fremdeles en lineær, men inhomogen på grunn av leddet på høyre side. Generelt vil den ha mange forskjellige løsninger avhengig av tilstanden til oscillatoren når kraften begynner å virke. Betrakter man to forskjellige løsninger og vil da differensen oppfylle den homogene ligningen. Den er uavhengig av kraften, men bestemt av begynnelsesbetingelsene. Kalles dette en «homogen løsning» vil hver løsning av den fulle ligningen kunne skrives som
Her er én bestemt, «partikulær løsning» av den inhomogene ligningen. Når oscillatoren er dempet, vil den homogene løsningen etter en stund gå mot null. Derfor er den stabile tilstanden til en drevet oscillatoren gitt ved den partikulære løsningen, uavhengig av begynnelsesbetingelsene.[4]
En partikulær løsning av en lineær differensialligning kan formelt finnes ved bruk av Greens funksjon. For det spesielle tilfellet at kraften varierer harmonisk med en viss frekvens, kan en eksplisitt løsning finnes. Etter en viss tid som er bestemt av dempningen, vil oscillatoren da begynne å svinge på en stabil måte. Når frekvensen til kraften nærmer seg egenfrekvensen ω0 til oscillatoren, kan amplituden til utslaget bli meget stort. Oscillatoren oppfører seg da som en resonator. Denne form for resonans er spesielt viktig for elektriske svingekretser og danner grunnlaget for all radioteknologi.[5]
Harmonisk kraft[rediger | rediger kilde]
Når kraften varierer med frekvens ω, kan bevegelsesligningen til oscillatoren skrives
hvor konstanten b angir styrken av den drivende kraften. Den partikulære løsningen vil nå svinge med samme frekvens ω, men med en ukjent amplitude a. Den kan beregnes ved å beskrive den ytre kraften som den reelle delen av den komplekse kraften f (t ) = b e-iωt. Det betyr at den søkte løsningen har den tilsvarende formen

hvor nå amplituden a i alminnelighet vil være kompleks. Det fysiske utslaget x(t ) er den reelle delen av denne komplekse funksjonen.
Når denne løsningsformen innsettes i differensialligningen, finnes amplituden som
Skriver man den komplekse nevneren i brøken som
med absoluttverdi og fasevinkel gitt ved blir dermed utslaget til den tvungne svingningen
Nevneren R blir mindre og mindre desto nærmere den påtrykte frekvensen ω er oscillatorens grunnfrekvens ω0. Det betyr at størrelsen til amplituden av utslaget øker til en maksimalverdi ved resonans der ω/ω0 = 1.
Oscillasjoner i flere retninger[rediger | rediger kilde]
Når oscillatoren bare kan svinge i en retning, kalles det en «endimensjonal harmonisk oscillator». Man kan lett inkludere muligheten for svingninger i flere retninger. Hvis for eksempel partikkelen med masse m er påvirket av fjærkrefter både i x- og y-retning, vil den totale kraften som virker på den være gitt ved vektoren
når man antar at fjærkonstantene i de to retningene har den samme verdien k. Skriver man ned Newtons andre lov, finner man den samme svingeligningen både i x- og i y-retning. Den totale bevegelsen er derfor gitt ved de kombinerte løsningene
som involverer fire integrasjonskonstanter. For passende begynnelsestidspunktet t = 0 er det alltid mulig å bestemme de slik at φx = 0. Herav følger at partikkelen følger i alminnelighet en ellipsebane i xy-planet hvor hovedaksen til ellipsen danner en vinkel med x-aksen som er bestemt av integrasjonskonstantene. Denne vinkelen er null hvis φy = π /2. Hvis i tillegg Ax = Ay , roterer partikkelen rundt på en sirkel med vinkelhastighet ω = √(k/m).

Den harmoniske kraften F som virker på partikkelen, er konservativ og kan derfor skrives som en gradient
hvor V er den potensielle energien eller potensialet. For denne todimensjonale oscillatoren har man derfor
som fremstiller en rotasjonsparaboloide i rommet.[4]
Tilsvarende, for en harmonisk oscillator som beveger seg i tre dimensjoner med samme fjærkonstant i alle retninger, er den potensielle energien
hvor r er posisjonsvektoren for partikkelen som beveger seg i dette potensialet. Oscillasjonene i alle tre retninger foregår med samme vinkelfrekvens ω og partikkelen beveger seg i alminnelighet på en ellipsoide.
Harmonisk oscillator som approksimasjon[rediger | rediger kilde]
Hvis et mekanisk system kommer litt ut av en likevektstilstand, vil det automatisk først søke tilbake til denne. Hvis den opprinnelige likevektstilstanden er «stabil», vil systemet da begynne å svinge harmonisk rundt denne. Dette er et generelt fenomen av stor praktisk og teoretisk betydning.[3]
Det kan illustreres ved å betrakte en partikkel med masse m som kan bevege seg i en dimensjon og er utsatt for en kraft F = -dV/dx fra et potensial V(x). En likevektsposisjon x0 er definert ved at kraften i dette punktet er null slik at partikkelen ikke får noen akselerasjon. Hvis man nå skriver potensialet som en Taylor-rekke utviklet rundt denne posisjonen, har man
Men her er nå det andre leddet lik null da likevektspunktet er definert ved at dV/dx skal være null der. Hvis man nå betrakter små utslag ξ = x - x0, kan høyere ordens ledd i Taylor-rekken antas å være neglisjerbare i forhold til leddet som inneholder den andrederiverte
Den er positiv hvis likevektsposisjonen er stabil. Potensialet tar da den approksimative formen
Mens det første leddet er bare en konstant som ikke spiller noen dynamisk rolle, er det andre leddet kvadratisk i utslaget ξ. Det betyr at bevegelsen til partikkelen blir en harmonisk svingning med en fjærkonstant som er lik med den dobbeltderiverte av potensialet. Vinkelfrekvensen blir dermed
Derimot, hvis den dobbeltderiverte hadde vært negativ, ville denne frekvensen da ha blitt imaginær som betyr at likevektsposisjonen ville ha vært ustabil da partikkelen ville ha beveget seg bort fra denne med økende hastighet.
Eksempel[rediger | rediger kilde]
Et eksempel på denne approksimasjonen er en svingende pendel med lengde l. Der er potensialet
hvor θ er utslaget fra likevektsposisjonen θ0 = 0 og g er tyngdeakselerasjonen. For små utslag θ << 1 kan nå potensialet approksimeres med
Da den kinetiske energien til pendelen er
- ,
blir derfor vinkelhastigheten for den harmoniske svingningen
Perioden til pendelen er uavhengig av utslaget i denne approksimasjonen. Men det er ikke lenger tilfelle for større utslag. For dette spesielle potensialet kan perioden beregnes for vilkårlig stort utslag ved bruk av elliptiske funksjoner. Svingningen er da fremdeles periodisk, men ikke lenger harmonisk.
Koblete oscillatorer[rediger | rediger kilde]

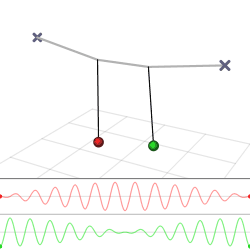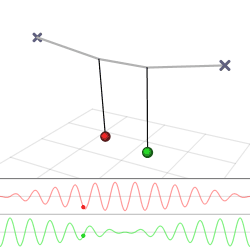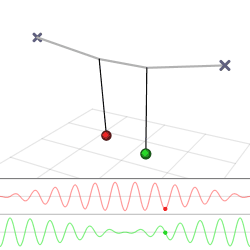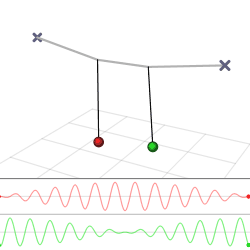
I mange sammenhenger vil en oscillator være koblet tll andre slik. Deres svingninger er derfor ikke lenger frie, men vil være påvirket av hverandre. Det enkleste eksemplet er to masser som kan bevege seg langs x-aksen og er forbundet med en fjær. Samtidig er hver av dem er koblet via to andre fjærer til hvert sitt faste punkt som vist i figuren. Her kan det antas at alle massene og fjærkonstantene er like store.
Hvis man kaller utslaget fra likevektsstillingen til den første massen for x1(t ) og utslaget til den andre for x2(t ), så blir forlengelsene til de tre fjærene henheoldsvis x1, x2 - x1 og - x2. De to massene vil derfor oppfylle bevegelsesligningene
De kan enkelt løses ved å legge dem sammen eller trekke dem fra hverandre. Da finner man de to ekvivalente ligningene
Hver av dem representerer en harmonisk oscillasjon, men med forskjellige frekvenser. Setter man u1 = (x1 + x2)/√2 og u2 = (x1 - x2)/√2, har man med en gang løsningene
De representerer hver en harmonisk svingning med en bestemt frekvens som er en egenfrekvens for systemet. Disse speseielle løsningene omtales derfor som egenmoder eller normalmoder.
De generelle løsningene for de to utslagene kan nå skrives som
og er lineærkombinasjoner av normalmodene. Man kan eksitere systemet ved tiden t = 0 i den første moden med frekvens ω1 ved å trekke begge massene like mye ut til siden. Da vil A2 = 0. Ved alle senere tidspunkt vil da x1(t ) = x2(t ). Begge masse svinger da synkront til den ene siden, så synkront sammen til den andre siden og deretter slik frem og tilbake. Denne moden sies å være «symmetrisk». Den andre moden med frekvens ω2 kan eksiteres ved å trekke de to massene ut til motsatte sider ved t = 0 slik at A1 = 0. De vil deretter fortsette å svinge med motsatte utslag slik at man alltid har x1(t ) = -x2(t ). Detter da en «antisymmetrisk mode».
Egenmoder fra matriser[rediger | rediger kilde]
Beregning av egenmoder for flere koblete oscillatorer gjøres mest systematisk ved bruk av matriser. En egensvingning er karakterisert ved at massene svinger med samme frekvens og fase. Med to masser antar man da at begge svinger som
hvor i = 1,2 og ai er foreløbig to ukjente konstanter. Settes dette inn i de to bevegelsesligningene, får man ligningsettet
etter å ha kansellert den felles cosinus-faktor og innført ω0 = √(k/m). Dette kan skrives på matriseformen
ved å definere vektoren a = (a1, a2) og matrisen
Denne er symmetrisk og vil derfor ha to reelle egenverdier som er de mulige egenfrekvensene. Verdiene finnes fra betingelsen
hvor I er 2 × 2 enhetsmatrisen. Skrevet ut, blir denne egenverdiligningen
hvis løsninger er gitt ved ω2 = 2ω02 ± ω02. Det gir de samme frekvensene ω1 og ω2 som funnet tidligere.
Etter å ha funnet egenfrekvensene kan man så beregne amplitudene a1 og a2 som inngår i vektoren a. For løsningen ω1 = ω0 blir a1/a2 = 1, mens for løsningen ω2 = √3 ω0 blir a1/a2 = -1. Det er hensiktsmessig å la disse to egenmodene være beskrevet ved enhetsvektorer slik at de dermed er
Disse to vektorene står vinkelrette på hverandre da a1⋅a2 = 0. Det er typisk for egenvektorer som tilhører forskjellige egenverdier.
Den generelle svingetilstanden for disse to massene er nå en lineærkombinasjon av disse to løsningene multipliert med vilkårlige konstanter A1 og A2. På den måten kan man skrive den som
hvor u1 og u2 er de tidligere funne egenmodene. Denne formen til den generelle løsningen kan tas over til å gjelde for et vilkårlig antall koblete oscillatorer.
Tre koblete oscillatorer[rediger | rediger kilde]
Når tre like store masser er koblet sammen med fjærer på samme måte, blir bevegelsesligningene
Egenverdiene blir dermed bestemt av matrisen
som igjen er symmetrisk. Den gir en tredjegradsligning for egenfrekvensene som i dette tilfellet forholdsvis lett lar seg løse med resultatet
De tilsvarende egenvektorene blir
når de ortonormeres slik at de tilfredsstiller ai⋅aj = δij uttrykt ved Kronecker-delta. Den generelle bevegelsen til de tre massene kan nå skrives som
når man innfører de tre uavhengige modefunksjonene u i(t ) = A i cos(ω it - φ i) hvor konstantene A1, A2 og A3 er bestemt av grensebetingelsene.
N koblete oscillatorer[rediger | rediger kilde]

En kjede med N koblete massepunkt hvor de to ytterste massene er koblet til faste punkt, kan tenkes som en del av en lengre kjede hvor utslagene x0 og xN+1 er lik med null. Et vilkårlig punkt i denne kjeden har da bevegelsesligningen[6]
For å finne modene må man i dette tilfellet finne egenverdiene til en N×N matrise. Her lar det seg gjøre ved å skrive utslagene i en bestemt mode på den tldligere formen xn(t ) = an cos(ωt - φ) hvor nå an er n-te komponent av egenvektoren a. Bevegelsesligningen kan da oppfylles ved å sette an = A sinKn hvor K foreløbig er en ubestemt konstant. Det verifiseres ved å sette inn denne antagelsen. Resultatet kan skrives som
og kan videre forenkles ved å bruke den trigonometriske identiteten for sinus til en sum av to vinkler. Det gir ω2 = 2ω02(1 - cos K) slik at
Dermed er egenfrekvensene bestemt hvis den ukjente K kan finnes. Den følger nå fra kravene a0 = aN+1 = 0 for en endelig kjede med N koblete massepunkt. Det første kravet er automatisk oppfylt med antagelsen an = A sinKn, mens det andre kravet gir K(N + 1) = mπ hvor heltallet m = 1, 2, ... ,N karakteriserer de forskjellige modene. Som ventet er det derfor ialt N egenmoder hvor hver kan tilordnes en verdi
og tilhørende egenfrekvens
For de korteste kjedene med N = 2 og N = 3 gir denne enkle formelen de tidligere funne egenfrekvensene. Også komponentene an = A sinKn til egenvektorene a kommer ut riktig for disse to tilfellene.[6] Den mest generelle bevegelse for det n-te massepunktet finnes nå ved å summere over bidragene fra alle modene,
hvor konstantene Am og φm bestemmes av grensebetingelsene til de N massepunktene som utgjør den endelige kjeden.
Tenkes de koblete massepunketene å legge veldig tett, vil kjeden i praksis være en elastisk streng som utfører longitudinale svingninger. Den generelle løsningen som her er funnet, representerer da en «stående bølge» til en svingende streng som er holdt fast i begge ytterpunktene. Størrelsen K tilsvarer «bølgetallet». Hver egenfrekvens vil kunne frembringe en tone hvis strengen er en del av et musikkinstrument.
Referanser[rediger | rediger kilde]
- ^ J.R. Lien og G. Løvhøiden, Generell fysikk for universiteter og høyskoler, Bind 1, Universitetsforlaget, Oslo (2001). ISBN 9788215000053.
- ^ M.L. Boas, Mathematical Methods in the Physical Sciences, John Wiley & Sons, New York (1983). ISBN 0-471-04409-1.
- ^ a b H. Goldstein, Classical Mechanics, Addison-Wesley Publishing Company, New York (1959).
- ^ a b c V. Barger and M. Olsson, Classical Mechanics: A Modern Perspective, McGraw-Hill Co., New York (1994). ISBN 0-07-003734-5.
- ^ P. Tipler, Physics for Scientists and Engineers, W. H. Freeman, New York (2004). ISBN 0-7167-0809-4.
- ^ a b D. Morin, Normal modes, Lectures at Harvard University (2010).
Litteratur[rediger | rediger kilde]
- R. Fitzpatrick, Damped Harmonic Oscillation, forelesninger ved University of Texas.
Eksterne lenker[rediger | rediger kilde]
- «Svingninger. Harmonisk oscillator», Forelesning i TFY4106, en del av serien: Fysikk. Av: Jon Andreas Støvneng, NTNU














































































