Sinuskurve
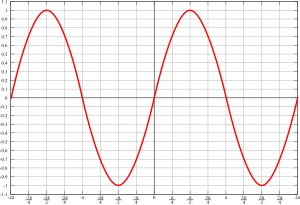
Sinuskurven, eller sinusoiden betegner formen til den grafiske fremstillingen av de to trigonometriske funksjonene sin(x) og cos(x), som begge er projeksjonen av et punkts bevegelse langs en sirkel.

Egenskaper[rediger | rediger kilde]
En sinuskurve er fullstendig beskrevet av to størrelser: avstanden mellom to topper i x-retning (kalt perioden) og avstanden fra midtlinja til maksimal- eller minimalverdien i y-retning (kalt amplituden).
Sinuskurven er spesielt viktig for å beskrive mekaniske og elektroniske bevegelsesfenomener, det vil si når x beskrives som tid. Da er avstanden mellom to topper lik periodetiden og er den inverse av frekvensen. t = 1/f.
Den deriverte av en sinuskurve beskriver stigningen til kurven, og den deriverte er også en sinuskurve.
Det er denne derivasjons-egenskapen som gjør at sinuskurven er allestedsnærværende innen elektronikk. Ingen annen kurveform kommer uforandret gjennom hvilket som helst nettverk av motstander, spoler og kondensatorer. Amplituden blir i allmennhet ikke uforandret.

Sinuskurven kommer også ut av differensialligningene for enkle oscillatorer med resonansegenskap, som masse-fjær -og spole-kondensator-systemer.
For praksiske beregninger er det svært viktig at den deriverte av en sinuskurve blir en cosinuskurve som har samme amplitude som sinuskurven. Dette letter regnearbeid betraktelig siden faktoren blir lik 1 ved operasjonen. Ved en bestemt sammenheng mellom x og frekvensmålet vil dette inntreffe: x = ω*t, der ω = 2*π*f. Dette kommer av at perioden til sin(x) har lengden 2*π i ren matematikk. Vinkelmålet 360°/(2*π) = 57.2958° har fått navnet radian og frekvensen ω måles i radianer per sekund. f er gitt i Hz, svingninger (perioder) per sekund.
Se også:
