Lineært ligningssystem
Et lineært ligningssystem er i matematikk et system av to eller flere lineære ligninger som inneholder de samme variablene.
Det følgende lineære systemet har tre ligninger med tre ukjente x, y og z:
Lineære ligningssystemer opptrer ofte med like mange ligninger som ukjente, og systemet kalles da kvadratisk. Et system med flere ligninger enn ukjente sies å være overbestemt, mens et underbestemt system har færre ligninger enn ukjente.
En løsning av ligningssystemet er et sett av verdier for de ukjente variablene som gjør at alle ligningene er simultant oppfylt. Lineære ligningssystem kan ha ingen, én eller uendelig mange løsninger. Eksemplet over har én løsning, gitt ved x = 4, y = 1 og z = 2,5.
Koeffisientene i lineære ligningssystem er ofte relle eller komplekse tall, og løsningen tilhører samme mengde av tall. Mer generelt vil teori og metoder for lineære ligningssystem være gyldig for koeffisienter og løsninger i en vilkårlig kropp.
Studiet av lineære ligningssystem har en lang historie i matematikk. Allerede på 1700-tallet ble Cramers regel funnet som gir løsninger ved bruk av determinanter. Også i moderne matematikk er teori for lineære ligningssystemer fundamental, studert i fagfeltet lineær algebra. Metoder for numerisk løsning av lineære ligningssystemer spiller en viktig rolle i mange fagfelt, som fysikk, kjemi, ingeniørvitenskap, informatikk og økonomi. Matematisk modellering i disse fagfeltene gir ofte opphav til komplekse ikke-lineære ligninger som ikke lar seg løse eksakt, men modelligningene kan likevel tilnærmes ved et sett av lineære ligninger. Lineære ligningssystem som har opphav i slike problemer kan inneholde flere millioner ukjente.
Elementært eksempel[rediger | rediger kilde]
Den enkleste formen for et lineære ligningssystem er to ligninger med to ukjente, som i det følgende eksemplet:
Ligningssystemet kan løses ved innsetting (kalt innsettingsmetoden) eller substitusjon, der den ene ligningen brukes til å uttrykke en variable ved hjelp av den andre:
Ved å sette inn uttrykket fra den første ligningen, kan den ukjente x nå elimineres i den andre:
Ligningen inneholder nå bare den ukjente y, og en finner lett løsningen y = 3. Deretter gir den første ligningen løsningen x = 7.
Generell form[rediger | rediger kilde]
Et generelt system av m lineære ligninger med n ukjente variabler kan skrives på formen:
Her er x1, x2, ...,xn de ukjente variablene, mens a11, a12,..., amn er koeffisientene i systemet. Høyresiden har konstantleddene b1, b2,...,bm.
Ligningssystemet er homogent dersom alle leddene på høyre side er lik null, det vil si dersom bi = 0 for i=1,....,m. Et system som ikke er homogent er inhomogent.
Vektorform[rediger | rediger kilde]
Et lineært ligningssystem kan skrives på vektorform, der de ukjent variablene er vekter til en lineærkombinasjon av kolonnevektorer:
Fra denne formen framkommer at ligningssystemet har en løsning hvis og bare hvis høyreside-vektoren b kan skrives som en lineærkombinasjon av koeffisientvektorene aj, j=1,...,n:
Matriseform[rediger | rediger kilde]
Et lineært ligningssystem kan også skrives på matriseform:
Her er koeffisientmatrisen A en (m×n)-matrise, x er en n-dimensjonal vektor, og b er en m-dimensjonal vektor.
Teori for lineære ligningssystemer er nært knyttet til teori for matriser. Ofte blir egenskaper til den tilhørende matrisen også brukt for å karakterisere et lineært ligningssystem, slik at matrisetypen og ligningstypen karakteriseres samtidig. For eksempel har et triangulært ligningssystem en triangulær matrise og et glissent ligningssystem har en glissen matrise.
Totalmatrisen til ligningssystemet er en matrise definert ved å legge til en ekstra kolonne i koeffisentmatrisen med elementer fra høyresiden i ligningssystemet:
Løsningsmengde[rediger | rediger kilde]

En løsning av et lineært ligningssystem er et sett av verdier for variablene i ligningssystemet som gjør at alle ligningene er simultant oppfylt. Mengden av alle mulige løsninger kalles løsningsmengden.
Tre ulike situasjoner kan opptre for et lineært ligningssystem:
- Systemet har uendelig mange løsninger
- Systemer har én entydig løsning
- Systemet har ingen løsninger
For et system med uendelig mange løsninger, kalles en bestemt løsning for en partikulærløsning. Et homogent system vil alltid ha null-løsningen definert ved at alle de ukjente er lik null. En løsning ulik null-løsningen kalles en egentlig løsning.
Geometrisk tolkning[rediger | rediger kilde]

I et lineært ligningssystem med to ligninger og to reelle ukjente vil hver ligning beskrive en linje i planet. Siden en løsning av et lineært ligningssystem må tilfredsstille alle ligninger simultant, er løsningsmengden gitt lik snittet mellom linjene. Løsningsmengden er dermed enten en linje, et punkt eller den tomme mengden.
For tre lineære ligninger med tre ukjente, vil hver ligning beskrive et plan i det tredimensjonale rommet og løsningsmengden er snittet av de tre planene. Løsningsmengden kan være et plan, en linje, et punkt eller den tomme mengden.
For n variabler representerer hver ligning et hyperplan i det n-dimensjonale rommet. Løsningsmengden er gitt som snittet av samtlige hyperplan.
Antall løsninger[rediger | rediger kilde]
Antall løsninger for et lineært ligningssystem bestemmes generelt av forholdet mellom antall ligninger og antall ukjente.
- Vanligvis vil et underbestemt system, det vil si et system med færre ligninger enn ukjente, ha uendelig mange løsninger.
- Vanligvis vil et kvadratisk system med like mange ligninger som ukjente ha én entydig løsning. Dette vil alltid være tilfelle dersom ligningene er lineært uavhengige. Er ligningene lineært avhengige, kan systemet ha uendelig mange løsninger.
- Vanligvis vil et overbestemt system, det vil si et system med flere ligninger enn ukjente, ikke ha noen løsning. Er ligningene lineært avhengige kan systemet imidlertid ha én eller mange løsninger.
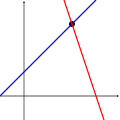
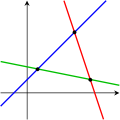
De følgende figurene viser de tre alternativene for et ligningssystem med to ukjente:
Gitt ved alle punktene på den blå rette linjen, har det første systemet uendelig mange løsninger. Gitt ved skjæringspunktet mellom de to fargede rette linjene, har det andre systemet én entydig løsning, Og siden de tre rette fargede linjene ikke har noe felles punkt, har det tredje systemet ingen løsning,
Figurene viser bare de vanligste tilfellene. Er to ligninger lineært avhengige, vil de tilhørende rette linjene være parallelle, og systemet kan ha ingen eller uendelig mange løsninger.
Romstruktur[rediger | rediger kilde]
Et homogent kvadratisk system gitt på formen:
vil ha egentlige løsninger hvis og bare hvis matrisen A er singulær. En egentlig løsning er en løsning der ikke alle de ukjente er lik null. Løsningsmengden vil da være et underrom av verdimengden til operatoren A, definert som nullrommet til operatoren. Dette kan beregnes ved Gauss-eliminasjon.
For et inhomogent kvadratisk system vil løsningsmengden enten være tom eller et affint rom. Vektorene i dette tilhører nullrommet til matrisen A. Dette løsningsrommet har derfor samme dimensjon som nullrommet.
Egenskaper[rediger | rediger kilde]
Uavhengighet[rediger | rediger kilde]
Kan ingen av ligningene utledes algebraisk fra de andre, er ligningene i et lineært ligningssystem lineært uavhengige. Når ligningene er lineært uavhengige, inneholder hver ligning ny informasjon om variablene. Fjernes en av ligningene, øker størrelsen på løsningsmengden.

Ligningene
er ikke lineært uavhengige—de er skalert med en faktor på to og er ligninger for den samme rette linjen i planet.
Et litt mer komplekst eksempel er gitt ved det følgende lineære ligningssystemet:
Ligningene er ikke lineært uavhengige, da den tredje ligningen er summen av de to første. En vilkårlig ligning av de tre kan utledes fra de to andre, og en av ligningene kan fjernes uten å endre løsningsmengden. Grafisk kan dette illustreres som tre rette linjer som krysser hverandre i et enkelt punkt.
Konsistens[rediger | rediger kilde]
Et lineært ligningssystem er konsistent om det har minst én løsning, ellers er det inkonsistent. Fra et inkonsistent system er det mulig å utlede en selvmotsigelse, som for eksempel at 0 = 1.
Et eksempel på et inkonsistent system er gitt ved ligningene:
Ved å subtrahere den første ligningen fra den andre, får en ligningen 6 = 0. Grafisk representerer ligningene to parallelle rette linjer.
Et ligningssystem der totalmatrisen T har høyere rang enn koeffisientmatrisen A vil være inkonsistent.
Ekvivalens[rediger | rediger kilde]
To lineære ligningssystemer er ekvivalente om de har samme sett av variable og det ene systemet kan utledes algebraisk fra det andre. Dette vil være tilfelle om begge systemene er inkonsistente, eller om enhver ligning i det ene systemet kan uttrykkes som en lineærkombinasjon av ligningene i det andre. To systemer er dermed ekvivalente hvis og bare hvis de har samme løsningsmengde.
Kvadratiske system[rediger | rediger kilde]
I et kvadratisk lineært ligningssystem er det like mange ligninger som ukjente, og koeffisientmatrisen vil være en kvadratisk (n×n)-matrise. Et slikt system vil ha en entydig løsning hvis og bare hvis determinanten til koeffisientmatrisen er ulik null. Matrisen er da ikke-singulær, og en invers av matrisen eksisterer. Løsningen kan dermed formelt skrives på formen:
- .
Et kvadratisk system med determinant ulik null, kalles et Cramersk ligningssystem, oppkalt etter den sveitsiske matematikeren Gabriel Cramer (1704-1752).
Underbestemte system[rediger | rediger kilde]
Et underbestemt system med færre ligninger enn ukjente, vil kunne ha uendelig mange løsninger. Den såkalte minste-kvadraters-løsningen er gitt som løsningen av ligningssystemet
der matrisen A nå har flere kolonner enn rekker. AT er den transponerte av koeffisientmatrisen til det opprinnelige ligningssystemet. Produktmatrisen (ATA) er en kvadratisk matrise, slik at minste-kvadraters-systemet har like mange ligninger som ukjente. Minste-kvadraters-løsningen eksisterer kun om matrisen (ATA) er ikke-singulær.
Løsningsmetoder[rediger | rediger kilde]
Det finnes en lang rekke metoder for å løse lineære ligningssystemer. Enkle systemer kan løses ved hjelp av substitusjon, som vist med det enkle eksempelet innledningsvis. Kvadratiske system kan løses ved Gauss-eliminasjon eller ved hjelp av Cramers regel.
Litteratur[rediger | rediger kilde]
- Fr. Fabricius-Bjerre (1977). Lærebog i geometri. Del 1: Analytisk geometri. Lineær algebra. Lyngby,: Polyteknisk forlag. ISBN 978-8-7502-0439-8.