Mengde
En mengde er i matematikk en veldefinert samling ulike objekter, betraktet som en helhet. Begrepet er et av de viktigste og mest grunnleggende i moderne matematikk, og teori for mengder kalles mengdelære. Mange andre matematiske størrelser blir definert ved hjelp av mengder.
Mengdelæren går tilbake til slutten av 1800-tallet, med Georg Cantor som en viktig bidragsyter. Hans definisjon av en mengde er «en samling av bestemte, forskjellige objekter, betraktet som et hele». Intuitive definisjoner av mengder fører imidlertid til uløselige paradokser, som for eksempel Cantors paradoks og Russells paradoks. Av den grunn lar man i aksiomatisk mengdelære være å definere begrepet mengde, men anser det som et udefinerbart grunnbegrep. I stedet brukes aksiomer til å beskrive hvilke egenskaper mengder har.
Elementene i en mengde[rediger | rediger kilde]
En mengde inneholder visse objekter, kalt elementer. Elementene kan i prinsippet være hva som helst, for eksempel tall, personer, biler, eller andre mengder. En mengde må være veldefinert: for ethvert objekt må det være mulig å avgjøre om objektet er med i mengden eller ikke. Hvis x er et element i mengden M, skriver man
At x ikke er et element i M kan skrives som
En mengde kan inneholde mer enn ett eksemplar av et element, men det andre eksemplaret vil være overflødig. Altså vil {a, b, b} være den samme mengden som {a, b}. Mengden kan inneholde et endelig eller et uendelig antall elementer.
Definisjonen av en mengde skrives ofte som et sett av klammeparenteser {}, med en beskrivelse av mengden mellom parentesene. Beskrivelse kan være en opplisting av elementene i mengden:
Flere etterfølgende punktum kan brukes istedenfor å liste alle elementene:
Alternativ kan mengden beskrives ved en regel P(x) som definerer elementene x:
Definisjonen kan leses som «Mengden M består av elementene x som oppfyller P». Et kolon blir også brukt som alternativ til den vertikale streken. Dersom en vil spesifisere en større mengde A som elementene tilhører, så kan definisjonen skrives som
Eksempler på regeldefinisjoner:
- Naturlige tall mindre enn 100:
- Definisjon ved operasjon mellom mengder:
En mengde kan også defineres rekursivt: 0 ∈ M, og hvis x ∈ M, så er x+1 ∈ M.
Mengden som ikke inneholder noen elementer, kalles den tomme mengden eller nullmengden og blir betegnet med ∅. En mengde som inneholder minst ett element er ikketom.
Delmengder[rediger | rediger kilde]

Hvis A og B er mengder, og ethvert element i A også er et element i B, så kalles A en delmengde eller en undermengde av B, og man skriver A ⊂ B. Dersom B i tillegg inneholder elementer som ikke er i A og A er ikke-tom, så er A er en ekte delmengde. Mengden {1, 2} har fire delmengder, den tomme mengden, {1}, {2} og {1, 2}. Bare {1} og {2} er ekte delmengder.
Hvis B også er en delmengde av A, må begge mengdene inneholde nøyaktig de samme elementene. Per definisjon er da A lik B, og man skriver A = B.
To delmengder er disjunkte dersom de ikke inneholder felles element. Mengdene {1,2} og {3,4} er disjunkte.
Mengder er ofte betraktet som elementer av en større fast mengde, kalt universalmengden.[1]
En partisjon av en mengde M er en oppdeling av mengden i disjunkte ikke-tomme delmengder, slik at alle elementene i M er medlem av én og kun én delmengde.
Operasjoner på mengder[rediger | rediger kilde]
Flere binære operasjoner kan defineres for mengder: Snitt, union, komplement og kartesisk produkt.[2]
Snitt[rediger | rediger kilde]

Mengden av elementer som er felles for A og B kalles snittet av A og B og betegnes A ∩ B.
Symbolet betegner «og». Snittet av mengdene {1,2,3} og {2,3,4} er lik {2,3}.
Snittet er en assosiativ og kommutativ operasjon:
Dersom A og B er disjunkte, så er snittet lik den tomme mengden.
Union[rediger | rediger kilde]

Mengden av elementer som enten er med i A eller i B (eller i begge) kalles unionen av A og B og betegnes A ∪ B:
Symbolet betegner «eller». Unionen av mengdene {1,2,3} og {3,4} er lik {1,2,3,4}.
Unionen er en assosiativ og kommutativ operasjon:
Komplement[rediger | rediger kilde]
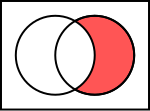
Komplementet til mengden A refererer til elementer som ikke er med i A. Det relative komplementet til mengden A i B er mengden av elementer i B som ikke tilhører A:
Komplementoperasjonen kan betraktes som en differanseoperasjon for mengder. Det relative komplementet til mengden {1,2,3} i {3,4,5} er mengden {4,5}. Mengden av irrasjonelle tall er det relative komplementet til mengden av rasjonale tall i mengden av reelle tall:
Dersom A tilhører en universalmengde M, så er det absolutte komplementet - eller bare komplementet - alle elementer som ligger i M, men ikke i A. Komplementet til A kan skrives AC eller A'.
Kartesisk produkt[rediger | rediger kilde]
Produktmengden eller det kartesiske produktet av to mengder A og B er mengden av alle ordnede par av elementer, (a,b), der a ∈ A og b ∈ B.[3] Produktet skrives A × B:
Definisjonen kan generaliseres til et endelig antall mengder: A × B × C × D.
Det todimensjonale rommet R2 kan defineres som det kartesisiske produktet av de reelle tallene R med seg selv: R2 = R × R.
Det kartesiske produktet er ikke kommutativt, det vil si at A × B generelt ikke er lik B × A.
Det kartesiske produktet er oppkalt etter den franske matematikeren René Descartes (1596-1650).
Relasjon mellom operasjoner[rediger | rediger kilde]
Det finnes mange satser og teorem som sier hvordan operasjonene relaterer seg til hverandre.[4] Dersom A, B og C alle er mengder, så gjelder distributive lover:
Dersom M også er en mengde, så gjelder også De Morgans lover:
Ordnede mengder[rediger | rediger kilde]
I en ordnet mengde M er det definert en binær relasjon betegnet med < , med de to følgende egenskapene:[5]
- Dersom både x ogy er elementer i M, så er ett og kun ett av de følgende utsagnene riktige:
- Dersom x, y og z alle er elementer i M, og i tillegg x < y og y < z, da er x < z.
Mengden av rasjonale tall Q er en ordnet mengde, der relasjonen x < y er definert til å bety at differansen ( y - x ) er positiv.
Venndiagram[rediger | rediger kilde]
Mengder og deres egenskaper kan også illustreres ved et såkalt Venndiagram. I dette blir universalmengden illustrert med en firkant, men denne blir også ofte utelatt. Ulike mengder og forholdet mellom disse blir illustrert ved areal innenfor universalmengden.
Venndiagram har blitt brukt over til å illustrere union, snitt og komplement. Illustrasjonsmåten ble introdusert omkring 1880 av engelskmannen John Venn (1834-1923).
Tallmengder[rediger | rediger kilde]
De viktigste tallmengdene er
- , mengden av naturlige tall
- , mengden av hele tall
- , mengden av rasjonale tall
- , mengden av reelle tall
- , mengden av komplekse tall
- , mengden av kvaternioner
- , mengden av oktonioner
Dersom elementene i en tallmengde kan kombineres ved multiplikasjon og divisjon, og resultatet er definert i samme mengden, så danner mengden en tallkropp. Mengden av reelle tall er en tallkropp. Mengden av naturlige tall er derimot ikke en kropp, da man ikke generelt kan dividere to hele tall med hverandre slik at resultatet også er et helt tall.
Se også[rediger | rediger kilde]
Referanser[rediger | rediger kilde]
- ^ R.D.Milne, 1980, s.4
- ^ R.D.Milne, 1980, s.5
- ^ H.F.Aas, 1974, s.6
- ^ H.F.Aas, 1974, s.4
- ^ W.Rudin, 1976, s.3
Litteratur[rediger | rediger kilde]
- Walter Rudin (1953, 1964, 1976). Principles of mathematical analysis. Singapore: McGraw-Hill International Book Co. ISBN 0-07-085613-3. Sjekk datoverdier i
|dato=(hjelp)
- Hans Fredrik AAs (1974). Forelesningsreferater i matematisk analyse. I. Bergen: Matematisk Institutt, Universitetet i Bergen.
- Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.




























