Determinant

Determinanten til en kvadratisk matrise er et reelt eller komplekst tall entydig bestemt av elementene i matrisa. Mer presist kan en si at determinanten er en funksjon med definisjonsmengde lik mengden av alle kvadratiske matriser og med verdimengde lik mengden av reelle eller komplekse tall.

Determinanten til matrisa A betegnes ofte det A eller det(A). Notasjonen |A| brukes også for determinanten, men det er lett å forveksle denne med absoluttverdien av matrisen. Ønsker en å presisere elementene i matrisa skrives determinanten vanligvis ved å omgi elementene med loddrette streker:

$\operatorname{det}\, A= \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nm} \end{vmatrix}$

Generelt kan determinanten defineres ved hjelp av Laplaces formel eller ved Leibniz’ formel, begge beskrevet i mer detalj i påfølgende avsnitt.

Eksempler

Volumet til dette parallellepipedet er absoluttverdien til determinanten av 3x3-matrisen som er formet av vektorene r1, r2 og r3.

2×2-matrise

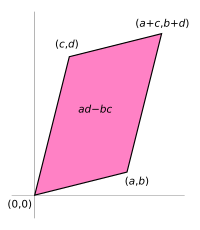
Determinanten til en 2×2-matrise A er definert ved

$\operatorname{det}\, A = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc$

3×3-matrise

Determinanten til en 3×3-matrise A er definert ved

$\operatorname{det}\, A=\begin{vmatrix}a&b&c\\ d&e&f\\g&h&i\end{vmatrix} = aei - afh - bdi + bfg + cdh - ceg.$

Sarrus’ regel er en metode for å huske denne formelen. Definerer en tre vektorer r1 = (a,b,c), r2 = (d,e,f) og r3 = (g,h,i), så er absoluttverdien av determinanten lik volumet utspent av de tre vektorene.

Definisjon ved Laplaces formel

La $\begin{vmatrix} a_{ij}\end{vmatrix}$ være determinanten til matrisa A, og la $M_{kl} = \begin{vmatrix} a_{ij}; k,l \end{vmatrix}$ være determinanten til den matrisa en får ved å stryke rekke k og kolonne l i den opprinnelige matrisa A. Determinanten $M_{kl}$ kalles minoren til matrise-elementet $a_{ij}$. Tilsvarende er kofaktoren $T_{kl}$ til matrise-elementet lik minoren med en fortegnsmodifikasjon:

$T_{kl} = (-1)^{k+l} \begin{vmatrix} M_{kl} \end{vmatrix} \,$

Laplace-ekspansjon av determinanten basert på en tilfeldig kolonne j er gitt ved

$\operatorname{det}\, A = \sum_{k=1}^n a_{kj} T_{kj}$

Tilsvarende formel gjelder for en tilfeldig rekke i:

$\operatorname{det}\, A = \sum_{k=1}^n a_{ik} T_{ik}$

Definisjon ved Leibniz’ formel

Leibniz’ formel for determinanten til en matrise A har forma

$\operatorname{det}\, A = \sum_{p \in S_n} \sgn(p) \prod_{i=1}^n A_{i,p(i)}.$

Summasjonen skal utføres over alle permutasjoner pav tallene {1, 2, ..., n}. En permutasjon er en funksjon som re-organiserer rekkefølgen til denne heltalsmengda. Fra kombinatorikk er det kjent at det eksisterer n fakultet n! = 1 · 2 · 3 · ... ·n slike permutasjoner. Mengden av alle permutasjoner er gitt betegnelsen S_n. For en vilkårlig permutasjon p definerer en signaturen sgn(p) lik +1 dersom permutasjonen er jamn og lik −1 dersom permutasjonen er odde.

Egenskaper

• Determinanten til en matrise der en kolonne eller en rad inneholder bare nullelement er lik null.

• Determinanten til en identitetsmatrise er lik 1.

• Dersom to rekker eller kolonner i matrisa bytter plass, så vil determinanten skifte fortegn.

• Dersom hvert element i en rekke eller en kolonne blir multipliser med en skalar k, så vil determinanten bli multiplisert med samme faktor.

• Determinanten er uendret dersom man til en rekke eller en kolonne adderer til et multiplum av en annen rekke eller kolonne.

• Determinanten til den transponerte matrisa $A^T$ er lik determinanten til matrisa A.

• Dersom to rekker eller kolonner i matrisa er lineært avhengige vil determinanten være lik null. Et spesialtilfelle av dette er dersom matrisa har to like rekker eller kolonner.

• En matrise er ikke-singulær hvis og bare hvis determinanten er ulik null.

• En matrise er invertibel hvis og bare hvis determinanten er ulik null.

• Similære matriser har lik determinant.

Bruk av determinanter

Løsningen til et lineært ligningssystem kan skrives eksplisitt ved hjelp av determinanter og Cramers regel.

Det karakteristiske polynomet $p(x)$ til matrisa A er definert ved ligningen

$p(x) = \operatorname{det}\, (A - Ix) \,$

der I er identitetsmatrisa med samme dimensjon som A. Røttene i det karakteristiske polynomet er egenverdiene til A.

Volumet til et parallellepiped utspent av tre vektorer er lik absoluttverdien av determinanten til 3x3 matrisa definert ved de tre vektorene.