Eulers tall

Eulers tall (/ˈɔɪlər/) er en matematisk konstant med en numerisk verdi som tilnærmet er lik 2,71828 og betegnes med bokstaven e. Denne betegnelsen ble gitt av den sveitsiske matematiker Leonhard Euler som oppdaget de fleste av tallets spesielle egenskaper. Den opptrer i mange grener av moderne matematikk på samme måte som konstantene π og i. De er knyttet sammen ved eiπ + 1 = 0 som er Eulers likhet.
Denne konstanten er et transcendentalt tall som kan defineres på mange måter. Den er grunntallet for naturlige logaritmer slik at lne = 1. Dermed er den også grunntallet for den naturlige eksponentialfunksjon ex som har den spesielle egenskapen at den er identisk med sin egen deriverte.
Euler selv skrev at denne konstanten er gitt ved uttrykket
der ∞ betegner et uendelig stort tall. Ved bruk av binomialformelen til Newton kan man herav utlede den uendelige rekken:
Denne og lignende rekker gjør det mulig å beregne en numerisk verdi for konstanten med så mange desimaler som man måtte ønske. Tar man med 50 siffer etter desimaltegnet, finner man
I noen sammenhenger omtales Eulers tall som Napiers konstant etter John Napier som utviklet det første system med logaritmer der denne konstanten opptrådte på en indirekte måte. Den må ikke forveksles med Euler-Mascheronis konstant γ.
Historie
[rediger | rediger kilde]Det som i dag kalles Eulers tall, opptrådte indirekte første gang i arbeidet Mirifici Logarithmorum Canonis Descriptio hvor John Napier innførte logaritmer i 1614. Han la merke til at for alle tallpar som skilte seg med en faktor 2, var differensen mellom deres logaritmer 6 931 469. Dette er nesten nøyaktig den naturlige logaritmen ln 2 = 0,6931 472 multiplisert med 10 000 000 da han regnet med heltall som var vanlig på den tiden.[1]

I den andre utgaven av Napiers verk som ble oversatt til engelsk av Edward Wright like før han døde i 1615, finnes det et tillegg som er en tabell med naturlige logaritmer. Det er uklart hvor den kom fra, men mest sannsynlig var William Oughtred opphavsmannen.[2]
På midten av 1600-tallet ble det klart at det var en direkte sammenheng mellom logaritmer og hyperbelen y = 1/x. Christiaan Huygens og andre kunne da definere den hyperbolske logaritmen ved integralet.
som er arealet under kurven for hyperbelen mellom 1 og x. Dette gjorde mulig en eksplisitt beregning av logaritmene til hvert positivt tall.
I et brev som Huygens mottok fra Gottfried Leibniz i 1690 blir det nevnt at dette arealet er 1 for et bestemt tall som han kalte b.[3] Det danner da grunntallet for de hyperbolske logaritmene og er akkurat slik som Euler noen tiår senere definerte samme tallet, men da betegnet med bokstaven e.[1]
Jakob og Johann Bernoulli
[rediger | rediger kilde]På samme tid arbeidet Jakob Bernoulli med matematikken rundt rentes rente. Hvis man for eksempel har 1 kr i banken med 100 % rente, vil dette beløpet bli 2 kr ved årets slutt. Men hvis renten blir lagt til hvert halvår, vil det bli (1 + 1/2)(1 + 1/2) = 2,25. Enda bedre er resultatet (1 + 1/4)4 = 2,44 hvis den blir lagt til ved slutten av hvert kvartal. Slik kan man fortsette og kan oppnå (1 + 1/365)365 = 2,71 når renten legges til hver dag. I grensen der den legges kontinuerlig til beløpet, vil det derfor bli
ved årets slutt når man benytter Eulers betegnelse for denne størrelsen. Bernoulli klarte ikke å finne dens nøyaktig verdi, men beviste i 1683 at den måtte være større enn 2 og mindre enn 3.[2]
Jakob Bernoulli hadde en yngre bror Johann Bernoulli som også var en anerkjent matematiker. Han undersøkte egenskaper ved eksponentialfunksjonen og var klar over at denne var den inverse til logaritmefunksjonen. I tillegg underviste han den unge Euler i matematikk.[4]
I 1714 benyttet Roger Cotes den uendelige rekken for e i sitt verk Logometria og beregnet tallet med 12 desimalers nøyaktighet.[5]
Leonhard Euler
[rediger | rediger kilde]
Fra 1727 da han var 20 år, var Euler ansatt ved Det russiske vitenskapsakademiet i St. Petersburg.[6] Samme år brukte han bokstaven e for konstanten 2,71828 i et manuskript om prosjektilers bevegelse. Den var definert ved at dens hyperbolske logaritme lne = 1. Denne notasjonen benyttet han også i et brev til Christian Goldbach i 1731 og i læreverket Mechanica som kom ut i 1736.[7]
Da Euler flyttet til Berlin i 1745, hadde han avsluttet sitt store verk Introductio in Analysin Infinitorum som ble utgitt først i 1748.[8] Her ga han en fullstendig fremstilling av alle viktige egenskaper ved e. Den numeriske verdien kunne han presentere med 23 desimalers nøyaktighet.[9]
Sammenhengen med den hyperbolske logaritmen følger fra dens deriverte. Fra definisjonen er
når man benytter analysens fundamentalteorem som forbinder derivasjon med integral, Men samtidig skal dette også følge fra en direkte beregning, det vil si
Men dette kan omformes til
når man skriver h/x = 1/n der n → ∞ når h → 0 og x holdes fast. Så når den hyperbolske logaritmen lne = 1, vil den deriverte av logaritmefunksjonen være ganske enkelt 1/x som er mest naturlig. Siden har hyperbolske logaritmer også blitt kalt naturlige logaritmer og betegnes vanligvis som ln x, loge x eller ganske enkelt log x når det ikke kan oppstå noen misforståelse.[10]
De faktiske årsakene til bruken av bokstaven e er ukjente, men det kan være fordi den er den første bokstaven i ordet eksponentiell. En annen mulighet er at e var den første ledige bokstaven da a, b, c og d kanskje ble brukt for andre størrelser. At Euler skulle ha brukt denne bokstaven med tanke på sitt eget navn, er lite sannsynlig.[7]
Definisjoner
[rediger | rediger kilde]Etter Eulers banebrytende arbeid i verket Introductio in Analysin Infinitorum fra 1748 hadde man mange ekvivalente definisjoner av e.[8] Ved å benytte binomialformelen på Bernoullis definisjon
fremkommer den uendelige rekken
som er absolutt konvergent. Den egner seg godt til en numerisk bestemmelse av konstanten.
Naturlig eksponentialfunksjon
[rediger | rediger kilde]Fra uttrykket for e finner man direkte for den naturlige eksponentialfunksjonen den uendelig rekken
Herav følger ved å derivere ledd for ledd at
slik at funksjonen er lik med sin egen deriverte.
Omvendt kan dette benyttes å til definere funksjonen. Den skal være en løsning av den enkle differensialligningen dy/dx = y med grensebvtingelsen y(x = 0) = 1. Da alle høyere deriverte dermed også vil være samme funksjon, finner man akkurat Taylor-rekken for den naturlig eksponentialfunksjon.[10]
Naturlig logaritmefunksjon
[rediger | rediger kilde]
Den inverse funksjon y(x) til eksponentialfunksjonen ex vil per definisjon måtte tilfredsstille
og er den naturlige logaritmefunksjonen y = ln x med e som grunntall slik at ln e = 1. Ved å derivere begge sider av ligningen ved bruk av kjerneregelen, finner man da
Den deriverte av logaritmefunksjonen er derfor dy/dx = 1/x som er utgangspunktet for den hyperbolske logaritmen. Ved denne formuleringen skrives funksjonen på den mest anvendelige form som
Når absoluttverdien |x | < 1, kan integranden utvikles i en geometrisk rekke som dermed kan integreres ledd for ledd. Det gir
som er praktisk for numerisk utregning av logaritmer. Rekken kan føres tilbake til Newton, men ble også utledet av Nicholas Mercator som har fått sitt navn knyttet til den.[1]
Kjedebrøker
[rediger | rediger kilde]Euler kunne i Analysin Infinitorum også definere verdien til e ved uendelige kjedebrøker. For eksempel er e = [2;1,2,1,1,4,1,1,6,1,1,8, .. ,1,1,2n, ...] eller mer eksplisitt
Denne er ekvivalent med formene
som igjen kan skrives på andre måter.[11]
Tallverdien til e er senere blitt uttrykt på mange andre måter ved forskjellige rekker og uendelige produkt.[12]
Kompleks eksponentialfunksjon
[rediger | rediger kilde]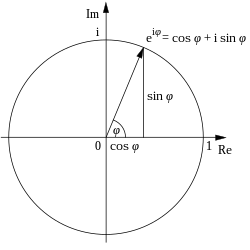
Da den uendelige rekken for ex er absolutt konvergent, kan funksjonen derfor utvides til å gjelde også for komplekse argument z = x + iy der i er den imaginære enheten definert som kvadratroten av -1. Generelt har man derfor
I det spesielle tilfellet at z er rent imaginær, det vil si z = iφ, splittes rekken i en reell og en imaginær del som begge kan uttrykkes ved trigonometriske funksjoner ved identiteten
Den kalles Eulers formel og ble også presentert av han i 1748. I dag anvendes den i mange forskjellige sammenhenger. For eksempel benyttes den til å fremstille periodiske svingninger og bølger som komplekse fasevektorer.
Det ekvivalente uttrykket
var blitt utledet av Roger Cotes allerede i 1714 fra en beregning av overflaten til en ellipsoide som han kunne gjøre på to forskjellige måter.[5] Men på den tiden var ikke sammenhengen mellom hyperbolske logaritmer og Eulers tall tilstrekkelig klarlagt for å skrive den på den mer kompakte formen som Euler fant senere.[4]
Når φ = π , gir formelen at
da cosπ = -1 og sinπ = 0. Dette magiske resultatet omtales vanligvis som Eulers likhet og er ekvivalent med ln(-1) = iπ .
Steiners problem
[rediger | rediger kilde]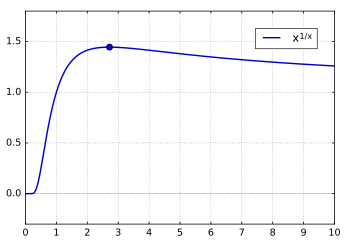
Den direkte sammenhengen mellom eksponentialfunksjonen og logaritmefunksjonen har mange praktiske anvendelser. Et eksempel er forbundet med den sveitsiske matematiker Jakob Steiner. Han viste rundt 1850 at Eulers tall kunne defineres som det positive, relle tallet x hvis x-te rot er størst mulig.[13] Det tilsvarer å vise at e er maksimum til funksjonen
som kan skrives om til
Ved et maksimum må den deriverte
være null. Det betyr at ln x = 1 som tilsvarer løsningen x = e. Maksimalverdien i dette punktet er e1/e som numerisk blir 1,444 667 861... .
På samme måte kan vises at funksjon xx har et minimum for x = 1/e.
Kuriositeter
[rediger | rediger kilde]
Da Google ble børsnotert i 2004, hadde de som mål å skaffe en kapital på $2 718 281 828.[14] For å skaffe seg nye medarbeidere med spesielle evner og interesse for matematikk, annonserte de ved flere kjente amerikanske universiteter ved å be potensielle søkere om å finne det første primtallet med 10 siffer i påfølgende desimaler til Eulers tall. Svaret var 7427466391 som begynner på 99. plass etter desimaltegnet. Klarte man denne oppgaven, ble man ledet til enda en av lignende type basert på hva som skjuler seg i den numeriske verdien til e.[15]
Donald Knuth som laget TeX, utviklet senere Metafont for å lage nye fonter. Dette programmet hadde versjonsnummer som var 2, 2.7, 2.71, 2.718 og så videre.[16]
Huskeregler
[rediger | rediger kilde]Det eksisterer mange tips for å huske de 16 første desimalene i e. For eksempel følger de første 16 fra 2,7 (disse må man huske selv) 1828 (Henrik Ibsens fødselsår) 1828 (Ibsens fødselsår igjen) 459045 (gradene i en rettvinklet, likebeint trekant er 45 grader, 90 grader og 45 grader) 2 (dette er den 16. desimalen, og er det samme sifret som vi begynte med og både π og e har 2 som 16. desimal).
Alternativt kan man se bort fra denne regelen over og fortsette den med 235 (første ustabile uranisotop), 360 en hel sirkel, 28 (Ibsens fødselsår forkortet) og 747 (Boeing flytype "Jumbojet").
På engelsk får man fra we require a mnemonic to remember e whenever we scribble math når man teller antall bokstaver i hvert ord som gir de første sifrene 2,71828 18284.
Referanser
[rediger | rediger kilde]- ^ a b c C.B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1968). ISBN 0-691-02391-3.
- ^ a b E. Maor, e: the Story of a Number, Princeton University Press, New Jersey (1994). ISBN 978-0-691-14134-3.
- ^ G. Leibniz, Brev fra Leibniz til Huygens, korrespondanse 1690.
- ^ a b C.E. Sandifer, How Euler Did Even More, The Mathematical Association of America (2015). ISBN 978-0-88385-584-3.
- ^ a b R. Cotes, Logometria, Philosophical Transactions of the Royal Society of London, 29(338), 5–45 (1714).
- ^ R. Calinger, Leonhard Euler: The First St. Petersburg Years (1727–1741), Historica Mathematica 23, 121–166 (1996).
- ^ a b F. Cajori, Use of the letter e to represent 2.718... i D. E. Smith, A Source Book in Mathematics, McGraw-Hill, New York (1929), archive.org online, pp 95-99.
- ^ a b L. Euler, Introductio in Analysin Infinitorum, Marc Michel Bousquet & Co, Lausanne (1748), archive.org online
- ^ L. Euler, Introductio in Analysin Infinitorum, Volume I, p. 90, e med 23 desimaler.
- ^ a b T. Lindstrøm, Kalkulus, Universitetsforlaget, Oslo (2016). ISBN 978-82-15-02710-4.
- ^ E. Sandifer, How Euler did it: Who proved e is irrational?, MAA Online, February 2006.
- ^ M.Abramowitz and I. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover Publications, New York (1964). ISBN 0-486-61272-4.
- ^ H. Dörrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover Publications, New York (1965). ISBN 0-486-61348-8.
- ^ S. Levy, In the Plex, Simon & Schuster, New York (2011). ISBN 978-1-4165-9658-5.
- ^ M. Kazmierczak, Google Billboard Problems, blogg (2004).
- ^ D. Knuth, The future of TeX and METAFONT, TeX Mag 5(1), 145 (1990).
Eksterne lenker
[rediger | rediger kilde]- A. Shell-Gellasch, Napier's e: Leonhard Euler, MAA Convergence (2010).
- E. Weisstein, MathWorld, e, Wolfram MathWorld.
- MacTutor, The number e, University of St. Andrews, Scotland.
- R. Wilson, The story of e, forelesning ved Gresham College (2007).









![{\displaystyle {\begin{aligned}e&=\lim _{n\to \infty }\left[1+{n \choose 1}{\Big (}{1 \over n}{\Big )}+{n \choose 2}{\Big (}{1 \over n}{\Big )}^{2}+{n \choose 3}{\Big (}{1 \over n}{\Big )}^{3}+\cdots \right]\\&=\lim _{n\to \infty }\left[1+{n \over 1!n}+{n(n-1) \over 2!n^{2}}+{n(n-1)(n-2) \over 3!n^{3}}+\cdots \right]\\&=1+{1 \over 1!}+{1 \over 2!}+{1 \over 3!}+{1 \over 4!}+{1 \over 5!}\cdots =\sum _{k=0}^{\infty }{1 \over k!}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba718be053f417f4403508f3cc9fdb4b880513a4)














