Naturlig logaritme

Naturlig logaritme til et positivt, reelt tall er logaritmen til tallet når grunntallet i logaritmen er Eulers tall e = 2.71828 1828 459... . I tillegg til å være reelt, er dette tallet også transcendentalt.
Generelt skrives den naturlige logaritmen av tallet x som ln x, loge x eller noen ganger når grunntallet e er underforstått, bare log x. Noen ganger omsluttes argumentet x med en parentes slik at man skriver ln(x ) eller loge (x ) istedet. Dette gjøres spesielt når argumentet er en sammensatt eller mer komplisert størrelse.
Enkelt sagt er den naturlige logaritmen til et tall x den potensen som e må opphøyes i for å gi tallet x. For eksempel, ln 7.5 er 2.0149... fordi 7.5 = e 2.0149.... Den naturlige logaritme til e er 1 fordi e 1 = e, mens den naturlige logaritmen til 1 er 0 da e 0 = 1.
Den naturlige logaritmen ln x kan betraktes som en reell funksjon av the positive argumentet x og kalles for den naturlige logaritmefunksjonen. Fra definisjonen følger at
for all reelle tall x > 0. Funksjonen er jevnt økende i dette åpne intervallet. Den naturlige logaritmefunksjonen er derfor den inverse av den naturlige eksponentialfunksjonen. Det er ekvivalent med at ln e x = x.
Ved bruk av naturlige logaritmer kan generelle logaritmer med andre grunntall lett regnes ut. For eksempel er de vanlige, briggske logaritmene med grunntall 10, lik med de naturlige logaritmene dividert med ln 10 = 2.302 585... . På den måten kan de spesielle og gunstige egenskapene til naturlige logaritmer overføres til bruk av logaritmer med andre grunntall.
Den naturlige logaritmefunksjonen kan utvides til å gjelde også for negative og komplekse argument. Men da er den generelt ikke lenger entydig, men spiller likevel en sentral rolle i kompleks analyse.
De naturlige logaritmene er tett knyttet til de opprinnelige, nepperske logaritmene som John Napier foreslo og beregnet i 1614. Men i stedet for grunntallet e, er disse basert på grunntallet 1/e. Denne logaritmen av et tall blir derfor mindre desto større tallet er. I tillegg hadde de den upraktiske egenskapen at logaritmen til 1 ikke var null. I noen sammenhenger blir også naturlige logaritmer kalt for nepperske, særlig i eldre litteratur.
Sentrale egenskaper[rediger | rediger kilde]

Fra definisjonen e ln x = x og egenskapene til den naturlige eksponentialfunksjonen, følger som forventet ln 1 = 0 og ln e = 1. På samme måte finner man
slik at
Ved å velge y = 1/x, har man da
da ln 1 = 0. I praksis betyr dette at logaritmer til små tall kan finnes fra de tilsvarende store, inverse tallene. For eksempel er ln 0.02 = - ln 50 = - 3.91 202... .
Det betyr at ln(x/y) = ln x - ln y. Likedan følger at lnx 2 = ln x⋅x = 2 ln x som kan utvides til å gi
for alle eksponenter p. Logaritmen er kvadratroten av et tall er halvparten av logaritmen til tallet, mens det kvadrerte tallet har en logaritme som er dobbel så stor.
Dette er sentrale egenskaper som karakteriserer alle logaritmer.[1]
Derivasjon og integrasjon[rediger | rediger kilde]
Den deriverte av den naturlige logaritmefunksjonen y = ln x finnes mest direkte ved å betrakte den inverse funksjonen x = e y. Da den deriverte av den naturlige eksponentialfunksjonen er funksjonen selv, vil dx/dy = e y = x. Herfra finnes nå den deriverte av logaritmefunksjonen som dy/dx = 1/(dx/dy) = 1/x eller
Ved å bruke kjerneregelen for derivasjon er derfor mer generelt
for en reell funksjon f(x ) > 0. Som et eksempel kan man betrakte den trigonometriske funksjonen sinx,
Ved å benytte analysens fundamentalteorem som forbinder derivasjon med integrasjon, har man nå at
hvor C er en vilkårlig integrasjonskonstant. For eksempel, så er
Det ubestemte Integralet av selve logaritmefunksjonen kan finnes ved delvis integrasjon,
Mer kompliserte integral hvor logaritmefunksjonen er multiplisert med en potens xn kan finnes på samme måte.[2]
Hyperbolsk definisjon[rediger | rediger kilde]
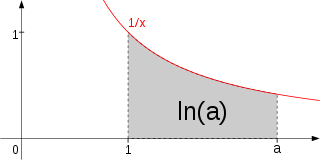
Verdien av den naturlige logaritmefunksjonen er gitt ved integralet
som tilsvarer arealet under hyperbelen y = 1/x fra x = 1 til x = a. Hvis a < 1, defineres arealet som negativt.
Det er mulig å definere den naturlige logaritmefunksjonen ved dette integralet.[3] Man kan lett verifisere at en slik fremgangsmåte vil gi funksjonen de ønskede egenskaper. For eksempel er
I det siste integralet på høyre side kan man innføre den nye integrasjonsvariable x' = ax. Det gir
hvorfra det meste følger. Før sammenhengen med eksponentialfunksjonen var kjent, ble denne geometriske definisjonen benyttet for den naturlige logaritmefunksjonen. Den ble derfor også omtalt som den hyperbolske logaritmefunksjonen.[4]
Rekkeutviklinger[rediger | rediger kilde]
Den hyperbolske definisjonen av den naturlige logaritmefunksjonen gjør det mulig å utvikle den i forskjellige, matematiske rekker. Skriver man den som
Når absoluttverdien |x | < 1, kan integranden skrives som en geometrisk rekke,
slik at man kan integrere hvert ledd i rekken for seg. Det gir
Isaac Newton utledet dette resultatet, men publiserte ikke beregningen da han oppdaget at Nicholas Mercator tidligere hadde funnet rekken. I ettertid er det derfor vanligvis Mercator som har fått navnet sitt knyttet til den.[4]
Rekken konvergerer langsomt og er derfor ikke så praktisk for numerisk beregning av logaritmer. Den konvergerer også for x = 1 og gir
Dette resultatet kan også benyttes til å beregne logaritmen til tall x > 1. Man dividerer det da så mange ganger n med 2 at det blir mindre enn 1 og benytter Mercators rekke på denne resten. På den måten finner man ln x = n ln 2 + ln(x/2n).
For x = - 1 ser man at rekken blir den negative av den harmoniske rekken
som er divergent. Tar man med de N første leddene i denne rekken, vil den vokse som ln N pluss Euler-Mascheronis konstant.[2]
Beregning av logaritmer[rediger | rediger kilde]
Ved å kombinere rekkene for ln(1 + x) og ln(1 - x) finner man
Denne rekken konvergerer raskere for |x| < 1 enn de to opprinnelige rekkene og kan benyttes til å regne ut naturlige logaritmer av tall som følger etter hverandre. Setter man x = 1/(2N + 1), blir da
Dermed får man for N = 1 direkte at
som med ganske få ledd gir en nøyaktig verdi. Denne prosessen kan fortsettes. Rekken for N = 2 konvergerer enda raskere og gir ln 3 = 1.098 612... . Fra disse to verdiene finner man så direkte ln 4 = 2 ln 2 samt ln 6 = ln 2 + ln 3. Slik kan man fortsette for større tall.
Generell definisjon[rediger | rediger kilde]
Bortsett fra Napiers opprinnelige logaritmer, kan man definere den generelle logaritmefunksjonen L(x ) for det reelle tallet x ved den sentrale egenskapen
Setter man her x = 0, ser man at funksjonen ikke eksisterer for denne verdien av argumentet. På samme måte med x = 1 vil L(1) = 0 slik at
som følger fra definisjonen ved å sette y = 1/x. Likedan gir y = x at L(x 2) = 2L(x) med dets generalisering til vilkårlige potenser.[3]
Mer informasjon om funksjonens egenskaper finnes i dens deriverte. Ved å holde x fast og så ta den deriverte av den definerende ligningen med hensyn på y, får man sammenhengen x L' (xy) = L' (y). Velger man her y = 1, har man rsultatat
hvor konstanten k = L' (1) bestemmer grunntallet for logaritmen. Når denne er positiv, er logaritmefunksjonen L(x ) jevnt økende for alle argument x > 0.
Eulers tall[rediger | rediger kilde]
Hvert valg av konstanten k tilsvarer et bestemt grunntall for logaritmen. Det enkleste valget k = 1 gir den naturlige logaritmefunksjonen. Den betegnes med ln x for argumentet x og er gitt ved integralet
Siden funksjonen er jevnt økende, finnes det et tall e slik at ln e = 1. Dette er Eulers tall og kan bestemmes ut fra kravet at den deriverte av den tilsvarende logaritmefunksjonen skal ha k = 1.[3]
Generelt for k ≠ 1 vil logaritmefunksjonen L(x ) være basert på et annet grunntall a. For å indikere dette, er det vanlig å betegne den samme funksjonen som loga(x ). Dens deriverte er per definisjon gitt som
Innfører man her 1/n = h/x, vil n → ∞ når h → 0 og x holdes fast. Dermed blir
hvor Eulers tall er definert som
Hvis man hadde valgt grunntallet å være a = e, ville loge(e ) = 1. Det er da naturlig å skrive funksjonen loge(x ) som ln(x ) med derivert 1/x.
Ved å ta den naturlige logaritmen av Eulers tall e = a logae, får man at (lna)logae = 1. Det betyr at den deriverte av logaritmefunksjonen for et vilkårlig grundtal a > 0 kan skrives som
Dette generelle resultatet danner grunnlaget for all videreutvikling av logaritmefunksjonens egenskaper.[5]
Eksponentialfunksjonen[rediger | rediger kilde]

Den generelle eksponentialfunksjonen E(x ) kan også defineres generelt for alle reelle argument x ved egenskapen
En direkte konsekvens er derfor at funksjonen er positiv for alle verdier av argumentet. Setter man her x = 0, resulterer det i E(0) = 1. Det spesielle valget y = - x gir dermed at
På samme måte finner man fra y = x at E(2x) = E(x )⋅E(x ) = E 2(x ) som kan generaliseres til
for en vilkårlig eksponent p. Hele funksjonen kan derfor genereres fra verdien for x = 1. Kalles denne for E(1) = a, har man dermed for den generelle eksponentialfunksjonen
Her er a grunntallet som nødvendigvis må være positivt. Den deriverte av funksjonen blir dermed
Hvis man derfor benytter det spesielle grunntallet a = e, er den deriverte av eksponentialfunksjonen funksjonen selv.[5]
Disse to funksjonene er invers til hverandre. Det betyr at
Er grunntallet i funksjonene a, tilsvarer dette at
Ved å derivere begge sider av ligningen med hensyn på x, finner man
Igjen gir dette den deriverte av logaritmefunksjonen som (d/dx) logax = 1/x lna og dermed bekrefter at den kan betraktes som den inverse til eksponentialfunksjonen.
Se også[rediger | rediger kilde]
Referanser[rediger | rediger kilde]
- ^ A. Søgaard og R. Tambs Lyche, Matematikk for Realgymnaset, Vol. II, Gyldendal Norsk Forlag, Oslo (1955).
- ^ a b M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions, Dover, New York (1972).
- ^ a b c T. Apostol, Calculus, Volume I, John Wiley & Sons, New York (1966). ISBN 0-471-00005-1.
- ^ a b C.B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1968). ISBN 0-691-02391-3.
- ^ a b R. Tambs Tyche, Matematisk Analyse I, Gyldendal Norsk Forlag, Oslo (1961).
Litteratur[rediger | rediger kilde]
- R. Courant, Differential and Integral Calculus, Volume I, Blackie & Son Limited, London (1961).






































