Matematisk konstant
En matematisk konstant er et spesielt tall, som oppstår naturlig og er av «særlig interesse av en eller annen årsak».[1] Konstanter oppstår innenfor mange felt i matematikk, med konstanter slik som e og som opptrer på så forskjellig områder som geometri, tallteori og matematisk analyse.
Hva det betyr at en konstant oppstår «naturlig», og hva som gjør en konstant «interessant», er til syvende og sist et spørsmål om smak, og noen matematiske konstanter er mer interessante av historiske årsaker enn av deres iboende matematiske interesse. De mest populære konstantene har blitt studert lang tilbake i tid og blitt beregnet til svært mange desimalplasser.
Alle matematiske konstanter er definerbare tall og vanligvis også beregnbare tall. (Chaitin's konstant er et viktig unntak).
Vanlige matematiske konstanter[rediger | rediger kilde]
Dette er konstanter som man vanligvis blir kjent med i grunnutdanningen i mange land.
Arkimedes konstant [rediger | rediger kilde]
Utdypende artikkel: Pi

Konstanten (pi) har en naturlig definisjon i Euklidsk geometri (forholdet mellom omkretsen og diameteren i en sirkel), men kan bli funnet mange andre steder i matematikken. Noen eksempel er gausiske integralet i sannsynlighetsregning og enhetsrøtter i tallteori. Tilstedeværelsen er imidlertid ikke begrenset til ren matematikk, forekommer i mange formler i fysikk og mange fysiske konstanter er naturlig definert ved at eller dens inverse er faktorisert ut. Det er grunn til å debattere hvorvidt slik tilstedeværelse er fundamental. Eksempelvis er lærebokdefinisjonen av den ikke-relativistiske bølgefunksjonen for grunntilstanden i hydrogenatomet
Hvor er Bohr radiusen. Denne formelen inneholder , men det er uklart om det er fundamentalt fra et fysisk perspektiv, eller om det bare reflekterer som er formelen for en kule med radius . Videre gir formelen bare en approksimasjon av den fysiske realiteten, siden den utelater spin, relativitet og den kvantefysiske naturen til et elektromagnetisk felt i seg selv. Likeledes er forekomsten av i formelen for Coulombs lov i SI-enheter avhengig av valget av enheter og ved en historisk slump ble konseptet permittivitet av vakuum introdusert i feltet elektromagnetisme av Giovanni Giorgi i 1901. Det er sant at når noen konstanter er valg i en relasjon så er fremtredenen av i andre relasjoner uunngåelig, men fremtredenen har alltid en matematisk årsak og ikke en fysisk årsak, slik som i eksempelt med hydrogenets bølgefunksjon.
Den numeriske verdien av er tilnærmet 3.1415926535 følge A000796 i OEIS. Å huske så mange siffer som mulig av er noe man forsøker rekorder i.
Eulers tall e[rediger | rediger kilde]
Utdypende artikkel: Eulers tall
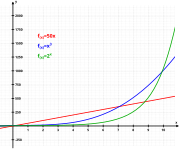
Eulers tall e, også kjent som eksponentiell vekst-konstanten, forekommer på mange felt i matematikken, og en mulig definisjon er verdien av det følgende uttrykket:
Eksempelvis oppdaget den sveitsiske matematikeren Jakob Bernoulli at e oppstår i rentes rente: En konto som starter med 1kr og får en årlig rente r med kontinuerlig rentes rente, vil akkumulere til er kroner på enden av året. Konstanten e har også anvendelser i sannsynlighetsteori, hvor den oppstår på en måte som ikke er åpenbart relatert til eksponentiell vekst. Anta at en spillemaskin med en til n sannsynlighet for å vinne blir spilt på n ganger. Da, for store n (slik som en million) vil sannsynligheten for at ingenting er vunnet gå mot 1/e og går mot denne verdien når n går mot uendelig.
En annen anvendelse av e, oppdaget delvis av Jacob Bernoulli sammen med den franske matematikeren Pierre Raymond de Montmort, et problem innen derangement, også kjent som hattinnsjekkingsproblemet.[2]. n gjester er invitert til en fest, og ved døren sjekker hver gjest inn en hatt med butleren som plasserer dem i merkede bokser. Butleren vet ikke navnet på gjestene, og må så putte dem i tilfeldig valgte bokser. Problemet til Montmort er: Hva er sannsynligheten for at ingen av hattene blir puttet i riktig boks. Svaret er
Når n nærmer seg uendelig, går dette mot 1/e.
Den numeriske verdien av e er tilnærmet 2.7182818284 følge A001113 i OEIS.
Referanser[rediger | rediger kilde]
- ^ Weisstein, Eric W. «Constant». MathWorld. Besøkt 13. april 2011.
- ^ Grinstead, C.M. «Introduction to probability theory». s. 85. Arkivert fra originalen 27. juli 2011. Besøkt 9. desember 2007.







