Elliptisk integral
Elliptisk integral er navnet som benyttes på en bestemt type integral som opptrer ved beregning av buelengden til en ellipse og i mange andre sammenhenger. De ble først systematisk studert av den franske matematiker Adrien-Marie Legendre og spilte en avgjørende rolle for Niels Henrik Abel og Carl Gustav Jacobi i deres etablering og utforskning av elliptiske funksjoner. Disse er inverse til de elliptiske integralene.
Matematisk sett sies et integral å være elliptisk når det har formen
hvor R(x,y) er en rasjonell funksjon og y2 = P(x) er et polynom av tredje eller fjerde grad. Integralet vil derfor inneholde kvadratrøtter av dette polynomet. Er graden til polynomet høyere, sies integralet å være hyperelliptisk.
De tre hovedtyper
[rediger | rediger kilde]Den generelle formen til et elliptisk integral er
hvor A, B, C og D er generelle polynomer, mens polynomet P har grad tre eller fire. Ved et skifte av integrasjonsvariabel kunne Lagrange i 1786 demonstrere at integralet med et tredjegrads polynom kunne overføres til et polynom av fjerde orden. I 1793 la Legendre frem et arbeid Mémoire sur les trascendantes elliptiques for det franske vitenskapsakademiet hvor han viste at alle slike integral kunne reduseres til tre hovedtyper.[1] Disse kan defineres på ulike måter med litt varierende notasjon.[2]
Første type
[rediger | rediger kilde]Det elliptiske integralet av første type kan skrives som
og er en funksjon av den øvre grensen x ≤ 1. Parameteren 0 < k < 1 kalles integralets modulus. Ved å innføre en ny integrasjonsvariabel t = sinθ, kan integralet alternativt skrives som
hvis den øvre grensen i integralet skrives som x = sinφ. Vinkelen φ kalles amplituden til integralet. Når denne tar sin maksimale verdi φ = π/2 som tilsvarer x = 1, har man det «fullstendige» integralet av første type,
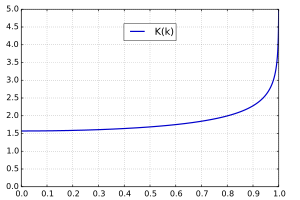
Ved å ekspandere integranden i en rekke med potenser av k2, kan verdien av dette integralet finnes fra
Alternativt kan det numeriske resultatet beregnes fra den aritmetisk-geometrisk middelverdi som
For å oppnå en viss nøyaktighet er denne metoden mye raskere enn å bruke rekkeutviklingen. Mens K(0) = π/2, er integralet logaritmisk divergent for k = 1.
Andre type
[rediger | rediger kilde]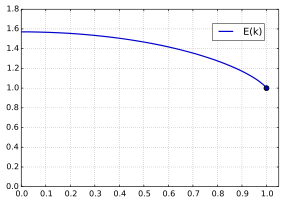
Det elliptiske integralet av andre type er definert som
Ved å innføre vinkelen φ som ny variable, kan det alternativt skrives som
Dermed er det fullstendige integralet av andre type gitt ved funksjonen
Ved en rekkeutvikling av integranden kan denne beregnes fra
Mens E(0) = π/2, er nå E(1) = 1 som sees direkte fra definisjonen. Dette fullstendige integralet gir omkretsen av en ellipse.
Tredje type
[rediger | rediger kilde]Det elliptiske integralet av tredje type er definert som
som alternativt kan skrives som
Her inngår en ny parameter n som kan ha en hvilken som helst verdi. Også for denne typen kan man definere et fullstendig integral på samme måte som for de to andre typene.
Buelengder av lemniskaten og ellipsen
[rediger | rediger kilde]Både lemniskaten og ellipsen har spilt en viktig rolle i utviklingen og den generelle forståelsen av elliptiske integral og elliptiske funksjoner. Mens beregning av buelengden til lemniskaten fremviste noen av de første, viktige egenskaper ved elliptiske integral, har beregning av buelengden til ellipsen gitt navnet til disse integralene. Mens hele omkretsen til lemniskaten er gitt ved et fullstendig elliptisk integral av første type, er omkretsen til ellipsen gitt ved det tilsvarende integralet av andre type.[3]
Lemniskaten
[rediger | rediger kilde]Ved bruk av polarkoordinater kan ligningen for en lemniskate skrives som r2 = 2a2cos 2θ. Her er 2a avstanden mellom dens brennpunkt som ligger på x-aksen symmetrisk om origo. Den delen av kurven som ligger i første kvadrant, utgjør en fjerdedel av hele kurven og er beskrevet ved at vinkelen θ varierer i intervallet 0 < θ ≤ π/4. Kvadratet ds2 = dr2 + r2dθ2 av den differensielle buelengden ds blir derfor
Buelengden til lemniskaten mellom origo og et punkt med polar vinkel θ' < π/4 er derfor gitt som
Dette integralet kan omskrives på standard Legendre form ved å innføre den nye integrasjonsvariable sinψ = √2 sinθ. Da er cosψ dψ = √2 cosθ dθ slik at buelengden er gitt ved det elliptiske integralet
med modulus k = 1/√2 og sinψ' = √2 sinθ' . Buelengden i første kvadrant tilsvarer θ' = π/4 som derfor betyr at ψ' = π/2. Hele omkretsen til lemniskaten er derfor gitt ved det fullstendige elliptiske integralet av første type som
Alternativt kan man benytte x2 = cos 2θ som ny integrasjonsvariabel. Den øvre grensen til integralet vil da tilsvare x' = 1 og
Det første integralet er gitt ved den lemniskatiske konstanten ω slik at Plem = 2ωa√2. Det kan derfor også betraktes som et fullstendig elliptisk integral av første type med modulus k2 = - 1 eller k = i = √-1 lik med den imaginære enhet. Man har derfor
som tilsvarer at K(1/√2) = √2 K(i ). På samme kan vises at E(i ) = √2 E(1/√2).
Ved å definere x = cos2φ i det siste integralet, ser man at uttrykket for omkretsen tar formen
- .
På denne formen kan integralet er gitt ved den aritmetisk-geometriske middelverdien av 1 og √2,
- .
Dette resultatet ble funnet av Gauss i 1800 og markerte begynnelsen på hans utforskning av elliptiske integral og funksjoner.[4]
Ellipsen
[rediger | rediger kilde]Ligningen for en ellipse med sentrum i origo og hovedakser a og b langs x- og y-aksen er
- .
Den kan parametriseres som x = a sinθ, y = b cosθ hvor vinkelen 0 < θ ≤ 2π . Kvadratet ds2 = dx2 + dy2 av den differensielle buelengden kan derfor skrives som
Lengden av buen mellom 0 < θ < θ' er derfor gitt ved et elliptisk integral av andre type,
- .
Modulus er lik med eksentrisiteten gitt som e 2 = 1 - b2/a2 .
Hele omkretsen til ellipsen kommer frem når den øvre grense θ' = 2π = 4 × π /2 og er derfor gitt ved fullstendige integralet
I grensen e → 0 går ellipsen over til å bli en sirkel med radius a. Da vil Pell → 2π a siden E(0) = π /2.
Legendres identitet
[rediger | rediger kilde]Ved direkte derivasjon av de fullstendige integralene K(k ) og E(k ) med hensyn på modulus k , finner man differensialligningene
- .
De kan kombineres til å gi en konsistensrelasjon som disse integralene på oppfylle. Ved å innføre den «komplimentære modulus»
- ,
samt de tilsvarende funksjonene K' (k ) = K(k' ) og E' (k ) = E(k' ), kan man vise at den deriverte dL/dk = 0 hvor L = KE' + EK' - KK' . Denne spesielle kombinasjonen av de fullstendige elliptiske integralene er derfor uavhengig av k og lik med en konstant. For å finne denne kan man for eksempel regne den ut i grensen k → 0 hvor integralene kan beregnes analytisk. Det gir identiteten
som første ble funnet av Legendre.[5]
For den spesielle verdi k = 1/√2 er K' = K og E' = E. Identiteten til Legendre reduseres da til (2E - K )K = π /2. Høyresiden kan nå forenkles siden
Ved å benytte at K(1/√2) = √2 K(i ) og E(i ) = √2 E(1/√2), har man da at
Dette spesielle resultatet var blitt funnet på en helt annen måte allerede i 1782 av Euler i forbindelse med hans utforskning av lemniskatens egenskaper.[6]
Addisjonsteorem
[rediger | rediger kilde]Det elliptiske integralet av første type opptrer i forbindelse med beregning av buelengden til lemniskaten. Allerede i 1754 hadde Euler vist at summen av to slike integral kunne skrives som et nytt integral av samme type og med samme modulus, men med en annen øvre grense.[7] Dette var et av de første eksempel på hva som Niels Henrik Abel senere generalisert til sitt berømte addisjonsteorem.
Mer konkret viste Euler at
hvor
Hvis disse integralene utvides til å gjelde i det kompleks planet, kan man i alminnelighet få ekstra termer på høyre side som kommer fra periodene de kan inneholde ved at integrasjonsveiene går rundt poler til integranden. Det er det samme som skjer i det enklere tilfellet når polynomet i kvadratroten i nevneren er av andre grad i stedet for fjerde grad som her.
Dette potensielle problemet unngås ved å innføre x = sinφ som Legendre gjorde. Da har man addisjonsteoremet
hvor nå
med
- .
Tilsvarende, men noe mer omstendlige addisjonsegenskaper har også de to andre typene av elliptiske integral.[2] Disse resultatene førte Legendre meget nær til oppdagelsen av elliptiske funksjoner. Dessverre for han ble han meget raskt innhentet og tilbakelagt på dette feltet av Niels Henrik Abel og Carl Gustav Jacobi.
Elliptiske funksjoner
[rediger | rediger kilde]Abel og Jacobi gjorde sin store gjennombrudd ved å invertere de elliptiske integralene. Det betyr at man betrakter den øvre grensen i integralet som en funksjon av integralets verdi. Denne funksjonen er en elliptisk funksjon. Jacobi tok utgangspunkt i den første typen med verdien F(x;k ) = u hvor u er en funksjon av x. Den «elliptiske sinusfunksjonen» defineres så som den inverse funksjonen til dette integralet, det vil si x = sn(u,k ). Med bruk av trigonometriske variable er derfor
og tilsvarende for den elliptiske cosinusfunksjonen
Disse er de to viktigste av Jacobis elliptiske funksjoner. I tillegg er det vanlig å definere
De oppfyller derfor relasjonene
og er generaliseringer av de trigonometriske funksjonene. Men i motsetning til disse som har perioden 2π , har de elliptiske funksjonene to perioder gitt ved de fullstendige integralene K og K' .
Addisjonsteoremet for integralet av første type som definere den elliptiske sinusfunksjonen sn(u,k ), kan nå skrives som u3 = u1 + u2. Det kan nå skrives som
når man for enkelhets skyld undertrykker den felles modulus k i alle funksjonene og skriver sn(u,k ) = snu. Denne identiteten tilsvarer den trigonometriske setningen for sinus til en sum av to vinkler. De andre elliptiske funksjonene tilfredsstiller tilsvarende addisjonsteorem.
Landens transformasjon
[rediger | rediger kilde]Ved å skifte integrasjonsvariable i de elliptiske integralene kan disse uttrykkes på andre måter. Spesielt viktig er Landens transformasjon som ble tatt i bruk av Legendre. Hvis man kaller den transformerte amplitude for φ1 og den transformerte modulus k1, så er sammenhengen med de opprinnelige verdiene φ og k gitt ved [1]
Dette kalles en «avtagende transformasjon» da den nye modulus er mindre enn den opprinnelige. Det følger fra
Sammenhengen mellom verdien til integralet før og etter transformasjonen sammenfattes i ligningen
Transformasjonen gir en reduksjon av modulus som er meget rask og k nærmer seg null etter en håndfull gjentagelser. I denne grensen kan integralet regnes ut analytisk.[2]
Spesielt enkelt blir dette for det fullstendige integralet som tilsvarer φ = π/2. Den transformerte amplituden blir da φ1 = π slik at K(k) = (1 + k1)K(k1). Gjentas så transformasjonen videre i det uendelige, vil man til slutt ende opp med en modulus som er lik null. Ved å benytte at K(0) = π/2 kan det fullstendige integralet regnes raskt ut fra
- .
De andre typene av elliptiske integral kan også beregnes numerisk ved den samme transformasjon.
Tas transformasjonen i motsatt retning, kan man gå til integral med større modulus. En slik «økende Landen-transformasjon» kan også benyttes i numeriske beregninger av de elliptiske integralene.[8]
Modulære transformasjoner
[rediger | rediger kilde]Under en avtagende Landen-transformasjon forandres den elliptiske modulusen k til
hvor k' er den opprinnelig, komplimentære modulus. Den nye blir
- .
En slik forandring av modulus i et elliptisk integral kalles en «modulær transformasjon». Da blir 1 + k1 = 2/(1 + k' ) eller
- .
Transformasjonen kan også inverteres slik at den opprinnelige modulus uttrykkes ved den transformerte. Det følger fra k' = (1 - k1)/(1 + k1) som gir
Av dette ser man at k1 forholder seg til k som k' til k1'. Fra sammenhengen K = (1 + k1)K1 mellom de fullstendige integralene vil man derfor også ha K1' = (1 + k ') K ' hvor det er naturlig å skrive K' = K(k' ) og K1' = K(k1'). Disse to resultatene kan kombineres til å gi
- .
som er typisk for en modulær transformasjon. For en økende Landen-transformasjon erstattes faktoren 2 med 1/2.[9]
Mer generelt kan man konstruere transformasjoner som erstatter faktoren 2 med andre primtall. Disse resultatene ble første initiert av Abel og Jacobi. I de følgende årene utviklet modulære transformasjoner seg til et meget stort og viktig del av algebraisk geometri basert på de periodiske egenskapene til elliptiske funksjoner.
Gauss' transformasjon
[rediger | rediger kilde]Samme modulære transformasjon kan fremkomme på forskjellige måter. Gauss fant et alternativ til Landens økende transformasjon ved å uttrykke integrasjonsvariablen θ i det elliptiske integralet av første type med den nye vinkelen ψ definert ved transformasjonen[9]
- .
Beregner man den deriverte av dette uttrykket, fremkommer igjen faktoren slik at man skrive
Her kan nå høyresiden forenkles ved å benytte identiteten
hvor den transformerte modulus er
- .
Derfor har man resultatet
som kan skrives mer kompakt som F(φ1,k1 ) = (1 + k )F(φ,k). Dette skiller seg med en faktor 2 fra resultatet for den tilsvarende Landen-transformasjonen. Men sammenhengen mellom amplitudene i integralene er også annerledes. Spesielt gir den at φ1 = π/2 når φ = π/2 slik at K1 = (1 + k )K som stemmer overens med hva som følger fra en økende Landen-transformasjon.
Hyperelliptiske integral
[rediger | rediger kilde]Elliptiske integral er bare en liten undergruppe av en mye større klasse av Abelske integral som Niels Henrik Abel undersøkte i sin store Paris-avhandling. Disse inneholder algebraiske funksjoner fra polynomligninger av vilkårlig høy grad. Da det så ut til at avhandlingen ble oversett eller var forsvunnet, så han seg nødt til å skrive en kortere versjon vel et år senere.[10] Den behandler den spesielle klassen av integral som involverer algebraiske funksjoner gitt ved y2 = P(x) hvor polynomet P(x) er av femte eller sjette grad. Abel viste at av disse er det to fundamentale integral med formen
hvor k = 1,2 og som oppfyller hans addisjonsteorem på en enkel måte. De kom snart til å spille en viktig rolle i den generalisering av elliptiske funksjoner som Jacobi lyktes med. Generelt når graden til polynomet P(x) er større enn fire, blir integral av denne sort omtalt som «hyperelliptiske».
Referanser
[rediger | rediger kilde]- ^ a b H. Hancock, Elliptic Integrals, John Wiley & Sons, New York (1917).
- ^ a b c M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, New York (1964). ISBN 0-486-61272-4.
- ^ R. Ayoub, The lemniscate and Fagnano's contributions to elliptic integrals, Archive for History of Exact Sciences, 29 (2), 131-149 (1984).
- ^ D.A. Cox, The arithmetic-geometric mean of Gauss, L’Enseignement Mathématique, 30, 275-330 (1984).
- ^ P. Duren, The Legendre Relation for Elliptic Integrals, in J. H. Ewing, F.W. Gehring, Paul Halmos: Celebrating 50 years of Mathematics, Springer-Verlag, New York (1991). ISBN 978-1-4612-6964-9.
- ^ G. Almkvist and B. Berndt, Gauss, Landen, Ramanujan, the Arithmetic-Geometric Mean, Ellipses, π, and the Ladies Diary Arkivert 4. august 2016 hos Wayback Machine., The American Mathematical Monthly, 95 (7), 585-608 (1988).
- ^ M. Kline, Mathematical Thought from Ancient to Modern Times, Volume 2, Oxford University Press, New York (1972). ISBN 0-19-506136-5.
- ^ A. Cayley, An elementary treatise on elliptic functions, Deighton, Bell and Co, Cambridge (1876).
- ^ a b H. McKean and V. Moll, Elliptic Curves: Function Theory, Geometry, Arithmetic; Cambridge University Press, Cambridge (1997). ISBN 0-521-65817-9.
- ^ N.H. Abel, Remarques sur quelques propriétés générales d’une certaine sorte de fonctions transcendantes, Journal für die reine und angewandte Mathematik, Bd. 3, 313-323 (1828).
Eksterne lenker
[rediger | rediger kilde]- Digital Library of Mathematical Functions, Chapter 19: Elliptic Integrals, National Institute of Standard and Technology (NIST).
- E. W. Weisstein, Elliptic Integral, Wolfram MathWorld.
- Wolfram Mathematica, Complete Elliptic Integrals.
- Encyclopedia of Mathematics, Elliptic Integral.






![{\displaystyle K(k)={\frac {\pi }{2}}\left[1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}k^{6}+\dots \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffbf6d189ce5ae3da043ef831335ac1925d32a89)




![{\displaystyle E(k)={\frac {\pi }{2}}\left[1-\left({\frac {1}{2}}\right)^{2}{\frac {k^{2}}{1}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {k^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {k^{6}}{5}}\cdots \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22b031cc4126019c8e36a74cabb268dfda62318c)











![{\displaystyle ds^{2}=a^{2}\cos ^{2}\theta d\theta ^{2}+b^{2}\sin ^{2}\theta d\theta ^{2}=a^{2}{\Big [}1-{\Big (}1-b^{2}/a^{2}{\Big )}\sin ^{2}\theta {\Big ]}d\theta ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0438e738c09ea9e0934b4bd013e0f32297b74d49)

































