Absoluttverdi

Absoluttverdien eller tallverdien til et reelt tall er i matematikk den numeriske verdien til tallet uten hensyn til fortegnet. For eksempel vil absoluttverdien til både 3 og -3 være lik 3. Absoluttverdien av et tall x skrives |x|.

Definisjonen av absoluttverdi kan også utvidest til å omfatte komplekse tall og begrepet modulus brukes da ekvivalent med absoluttverdi.

For vektorer i et endelig-dimensjonalt vektorrom brukes ofte betgnelsen absoluttverdien av vektoren som synonym for den euklidske vektornormen. Dette svarer til den geometriske lengden til vektoren.

Absoluttverdien kan også defineres formelt som en funksjon definert på en ordnet ring.

Absoluttverdien av reelle tall

Absoluttverdi-funksjonen for reelle tall.

Formell definisjon

Absoluttverdien av et reellt tall er definert som funksjonen f: R $\rightarrow$R⁺ gitt ved

$f(x) =\left\{\begin{matrix} x, & x \ge 0 \\ -x, & x < 0 \end{matrix}\right.$

Funksjonen skrives vanligvis som f(x) = |x|.

Absoluttverdien kan alternativt defineres som funksjonen

$|x| = \sqrt{x^2}. \,$

Fundamentale egenskaper

Absoluttverdien for reelle tall har følgende fundamentale egenskaper:

$\begin{alignat}{2} &|a| \ge 0 \\ &|a| = 0 \iff a = 0 \\ &|ab| = |a||b|. \\ \end{alignat}$

Trekantulikheten

Trekantulikheten har forma

$|a+b| \le |a| + |b|.$

En nedre grense for absoluttverdien av en sum er gitt ved

$| \; |a| - |b| \; | \le |a+b|.$

Disse skrives ofte sammen som

$| \; |a| - |b| \; | \le |a+b| \le |a| + |b|.$

Derivert

Den deriverte av absoluttverdifunksjonen for positive verdier av argumentet er lik 1, og for negativ verdier lik -1. Den deriverte er ikke definert i vanlig forstand i punktet x = 0, der funksjonen har et knekkpunkt. I en utvidet klasse av distribusjoner er den deriverte av absoluttverdifunksjonen definert overalt lik tegnfunksjonen, definert som

$\sgn(x) = \begin{cases} -1 & \text{if } x < 0, \\ 0 & \text{if } x = 0, \\ 1 & \text{if } x > 0. \end{cases}$

Antiderivert

Absoluttverdifunksjonen er integrerbar og den antideriverte er gitt ved

$\int|x|dx=\frac{x|x|}{2}+C.$

Intervalldefinisjon med absoluttverdi

Et åpent intervall av relle tall blir ofte definert ved hjelp av absoluttverdifunksjonen som

$D_1 = \left \{x| \; |x-a| < b \right \} \,$

Her er a midtpunktet i intervallet, og lengden av intervallet er lik 2b. Et lukket intervall defineres tilsvarende som

$D_2 = \left \{ x| \; |x-a| \le b \right \} \,$.

Absolutt konvergens for rekker

En rekke $\sum a_n$ sies å konvergere absolutt dersom rekken $\sum | a_n |$ konvergerer. Dersom $\sum a_n$ konvergerer, mens $\sum | a_n |$ divergerer, sies rekken å konvergere betinget.

Absoluttverdien av komplekse tall

Formell definisjon

Argand-diagram for det komplekse tallet z = (a,b) = a + ib.

Absoluttverdien eller modulus til et komplekst tall er definert som funksjonen f: C $\rightarrow$R⁺ gitt ved

$|z| = \sqrt{zz^*}= \sqrt{(\text{Re}\; z)^2 + (\text{Im}\;z)^2} \,$

Her er z ^* er den kompleks konjugerte av z. Videre er Re z lik realdelen av z og Im z er imaginærdelen. Dersom imaginærdelen er lik null samsvarer definisjonen for komplekse tall med definisjonen for reelle tall.

Geometrisk tolkning

Ved hjelp av absoluttverdien, samt polarvinkelen ϕ kan ethvert komplekst tall skrives på eksponetialformen

$z = |z| e^{i \phi},\,$

I et Argand-diagram, der et komplekst tall representeres ved et punkt i et to-dimensjonalt koordinatsystem, svarer absoluttverdien av det komplekse tallet til lengden av vektoren fra origo til punktet. I figuren til høyre er |z| = r.

Egenskaper

De samme fundamentale egenskapene gjelder for komplekse tall som for reelle tall. Også trekantulikheten har samme form. I tillegg gjelder relasjonene

$|z| \ge |\text{Re}\; z| \ge \text{Re}\; z \;$

$|z| \ge |\text{Im}\; z| \ge \text{Im}\; z \;$

Absoluttverdien av vektorer

Geometrisk illustrasjon av trekantulikheten for vektorer.

Formell definisjon

For vektorer i et endelig-dimensjonalt euklidsk vektorrom definerer en del lærebøker absoluttverdien til en vektor til å være lik normen til vektoren. For en koordinatvektor v = (x,y,z) i et tre-dimensjonalt rom er aboluttverdien da definert ved

$|v| = ||v||_2 = \sqrt{x^2 + y^2 +z^2} \,$

Absoluttverdien er da lik den geometriske lengden av vektoren.

Egenskaper

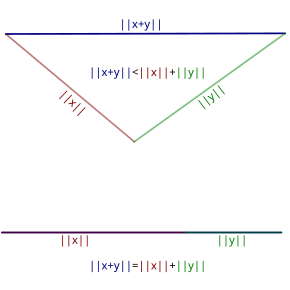
Trekantulikheten gjelder for vektorer på samme form som for relle tall. Den geometriske tolkningen av denne ulikheten er at den korteste veien mellom to punkt er en rett linje. Den geometriske illustrasjonen av trekantulikheten viser øverste et eksempel med streng ulikhet, nederst et eksempel med likhet i relasjonen.

Absoluttverdi av matriser

Formell definisjon

Absoluttverdien til en matrise A = {a_ij} betegnes med |A| eller |A|_abs og er definert lik en matrise med elementer lik absoluttverdien av elementene i den opprinnelige matrisen:

$|A|_{abs} = \begin{bmatrix} |a_{11}| & |a_{12}| & \cdots & |a_{1m}| \\ |a_{21}| & |a_{22}| & \cdots & |a_{2m}| \\ \vdots & \vdots & \ddots & \vdots \\ |a_{n1}| & |a_{n2}| & \dots & |a_{nm}| \end{bmatrix}$

En del lærebøker bruker |A| som notasjon for determinanten til A.

Egenskaper

Trekantulikheten gjelder også for absoluttverdien av matriser:

$|A+B|_{abs} \le |A|_{abs} + |B|_{abs} \;$

Dersom matriseproduktet AB er definert, så er

$|AB|_{abs} \le |A|_{abs} |B|_{abs} \;$

Diverse

I programmeringsspråk kalles absoluttverdifunksjonen ofte abs().

Litteratur

• Fr Fabricius-Bjerre (1949, 1968, 1977). Lærebog i geometri. I: Analytisk geometri, lineær algebra. Polyteknisk forlag, Lyngby. ISBN 97-502-0440-8.

• Helmut Lütkepohl (1996). Handbook of Matrices. John Wiley and Sons, Chichester. ISBN 0-471-97015-8.

Eksterne lenker

• Absoluttverdi (definisjon) - matematikk.net