Hippokrates fra Khíos
| Hippokrates fra Khíos | |||
|---|---|---|---|
| Født | 470 f.Kr. Khios | ||
| Død | 410 f.Kr. | ||
| Beskjeftigelse | Matematiker, astronom, filosof | ||
Hippokrates fra Khíos (gresk: Ἱπποκράτης ὁ Χῖος, født ca. 470, død 410 f.Kr.) var en gresk matematiker fra øya Khíos. Han arbeidet spesielt med geometriske problem som var av størst interesse i antikkens Hellas. I denne forbindelse skrev han en av de første lærebøker i geometri. Av egne bidrag huskes best hans forsøk på å løse problemet rundt sirkelens kvadratur og kubens fordobling, men uten å lykkes. Derimot viste han at arealet av spesielle figurer avgrenset av to sirkelbuer kunne beregnes geometrisk. Disse halvmåneformede figurene har senere fått navnet Hippokrates' luner.
Hippokrates var også opptatt med spørsmål innen astronomi. I forbindelse med observasjoner mente han at vi kan se ved at lysstråler blir sendt ut fra øyet. Dette var også Platon for, men Aristoteles argumenterte for at de ble mottatt av øyet.
Vitenskapelig liv[rediger | rediger kilde]
Da Hippokrates vokste opp på Khíos, er det sannsynlig at han tidlig ble kjent med arbeidene til Pythagoras da denne kom fra naboøya Samos. Dette kan ha vært en medvirkende årsak til at han tok interesse i logiske bevis og innførte i denne sammenhengen metoden med reductio ad absurdum. Forskjellige beretninger sier at han viet seg fullstendig til løsning av geometriske problem etter at han hadde opplevd flere mislykkede pengetransaksjoner.
Hippokrates skrev den første, kjente lærebok i geometri.[trenger referanse] Den het Elementer (gresk: Στοιχεῖα, Stoicheia) og inneholdt fundamentale definisjoner og teorem som andre senere kunne bygge videre på. Euklid kalte knapt hundre år senere også sitt læreverk i geometri for Elementer. Hippokrates var den som begynte å betegne punkter med bokstaver som A, B og C, slik at et triangel kunne omtales som figuren ABC.
Kubens fordobling[rediger | rediger kilde]
På den tiden Hippokrates levde var et av de største problemene innen geometrien å finne sidekanten i en kube med dobbelt så stort volum som en gitt kube. Løsning av denne oppgaven fikk derfor navnet kubens fordobling. Den tilsvarende oppgaven med et kvadrats fordobling visste man kunne løses ved å konstruere mellomproporsjonalen eller det geometriske middel av tallene 1 og 2. Dette ledet Hippokrates til å vise at fordobling av kuben kunne løses ved å finne to mellomproporsjonaler mellom de samme tallene. Hvordan dette skulle gjøres i praksis, visste han ikke. Men likevel var dette resultatet avgjørende da Menaikhmos senere viste at disse mellomproporsjonalene var gitt som skjæringspunkt mellom forskjellige kjeglesnitt.
Hippokrates' luner[rediger | rediger kilde]

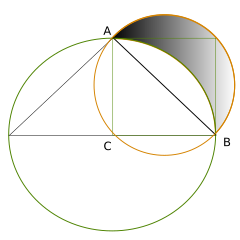
Tidligere hadde Hippokrates arbeidet med å finne arealet innenfor en sirkel. Dette ble formulert som å finne et kvadrat med like stort areal, noe som medførte at problemet blir omtalt som sirkelens kvadratur. I denne forbindelsen oppdaget han at visse deler av sirkelflaten kunne beregnes eller konstrueres. Disse så ut som sigder og blir nå kalt for luner da formen minner som halvmåner.
Senter til halvsirkelbuen ligger i punktet D som er midtpunktet til diameteren AB i denne mindre halvsirkelen. Men nå er linjestykket AB en faktor √(2) mindre enn diameter AC i den store halvsirkelen. Derfor er arealet av halvsirkelen med senter i D halvparten av arealet til den større sirkelen med senter i O, det vil si lik med arealet av kvadranten AFBO. Da disse to arealene begge inneholder segmentet AFBD, betyr det at arealet til Hippokrates' skraverte lune AFBE er lik med arealet til den skraverte trekanten ABO.
Dette resultatet viste at en del av arealet til sirkelflaten kunne uttrykkes som arealet til en trekant, det vil si ved konstruerbare tall. Da arealet av hele sirkelflaten er gitt ved størrelsen π, ga dette håp om at denne kunne uttrykkes som et rasjonelt tall. Etter omtrent to tusen år viste det seg at dette ikke var mulig, π er et transcendentalt tall.

Ved å bruke Pytagoras’ læresetning for den grønne, rettvinklete trekanten i figuren til høyre, har man at summen av kvadratene til diameterene i de to, røde lunene er gitt ved kvadratet til diameteren i halvsirkelen som går gjennom hjørnepunktene A, B og C,
Da arealene til hver av halvsirklene på trekantens sider er proporsjonale med kvadratene av de tilsvarende diametrene, følger direkte ved samme argumentasjon som over for en lune, at summen av arealene til to to røde lunene er lik med arealet til den grønne trekanten.
Litteratur[rediger | rediger kilde]
- Viggo Brun, Alt er tall, Universitetsforlaget, Oslo (1994). ISBN 82-13-00151-6.
- Carl B. Boyer, A History of Mathematics, Princeton University Press, New Jersey (1985). ISBN 0-691-02391-3.
Eksterne lenker[rediger | rediger kilde]
- MacTutor, Hippocrates of Chios, University of St. Andrews, Scotland.

