Trekanttall

Trekanttall er figurtall basert på den geometriske formen til en likesidet trekant. De utgjør en heltallsfølge hvor det n-te tallet betegnes med Δn eller Tn. Tallet angir antall prikker eller kuler som kan arrangeres som en slik trekant med n prikker langs hver side. De første er
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190 osv
Tallene tilhører den større klassen av polygontall som er basert på regulære mangekanter med flere sidekanter enn i trekanten. Av disse er kanskje kvadrattallene mest kjent.
Hvert trekantall Δn består av summen av de n første naturlige tallene. Videre er summen av de n første trekanttallene det n-te tetraedertallet. Denne egenskap viser at de også tilhører en annen klasse av figurtall som kalles simplekstall og kan leses direkte ut fra Pascals trekant.
Aritmetiske egenskaper[rediger | rediger kilde]
De fem første trekanttallene kan illustreres ved prikkene i trekantene
| 1 | 3 | 6 | 10 | 15 | 21 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
Man ser at hvert trekanttall Δn er summen av det forrige trekanttallet Δn-1 pluss et linjestykke (eller «tokant») med n prikker. Derfor kan de beregnes fra rekursjonsrelasjonen

med utgangspunktet at Δ1 = 1. Det gir Δ2 = 1 + 2 = 3, Δ3 = Δ2 + 3 = 1 + 2 + 3 = 6 og så videre. Generelt er derfor det n-te trekanttallet gitt ved summen
da den utgjør en enkel, aritmetisk rekke. Alternativt kan dette utledes ved induksjon. Formelen er gyldig for n = 2. For n + 1 har man fra rekursjonsformelen
som bekrefter uttrykket for Δn.
Dette har også et enkelt, geometrisk innhold. Hvis man kombinerer prikkene til to trekanter med Δn prikker i hver, kan man lage et rektangel med sider bestående av n og n + 1 prikker. Derfor er 2Δn = n(n + 1) som gir formelen.
Summen av to påfølgende trekanttall[rediger | rediger kilde]
Hvis man legger sammen to trekanttall som følger etter hverandre, får man et kvadrattall. For eksempel er 3 + 6 = 9 = 32 og 10 + 15 = 25 = 52.
Det kan også vises geometrisk som illustrert i de følgende figurene hvor prikkene fra de to trekantene alltid kan kombineres til å danne et kvadrat,
| 4 | 9 | 16 | 25 | 36 | ||||
|---|---|---|---|---|---|---|---|---|
| |
|
|
|
Matematisk følger dette resultatet for addisjon av påfølgende trekanttall ved ligningen
Summasjon av trekanttall[rediger | rediger kilde]
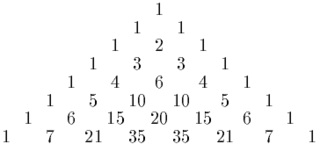
På samme måte som at summen av de n første, naturlige tallene er det n-te trekanttallet, er summen av de de n første trekanttallene er nytt figurtall. I dette tilfellet er det et tetraedertall Tn basert på et tetraeder med samme form som en pyramide. Tetraedertallene er derfor også del av en større klasse som kalles pyramidetall.
Både trekanttallene og tetraedertallene kan leses ut av Pascals trekant. Mens de første ligger på den andre linjen som går fra toppunktet i denne trekanten ned mot venstre, ligger tetraedertallene på den neste, parallelle linjen. De første er 1, 4, 10, 20, 35, etc. Mens summen av de tre første trekanttallene er 1 + 3 + 6 = 10 som er det tredje tetraedertallet, er summen av de fire første 1 + 3 + 6 + 10 = 10 + 10 = 20 som er det fjerde av disse figurtallene. Generelt har man
Geometrisk kan man forstå dette resultatet ved at det n-te tetraedertallet Tn er antall prikker eller kuler i en pyramide med en likesidet trekant som grunnflate med n kuler i hver av de tre sidene. Denne flaten inneholder derfor Δn kuler. I etasjen over ligger det en kule i hver fordypning til laget av kulene under, det vil si Δn-1 kuler. Slik fortsetter lagene i pyramiden til toppen hvor det ligger Δ1 = 1 kule. Dette tilsvarer rekursjonssrealsjonen
Ut fra plasseringen i Pascals trekant, kan det n-te trekanttallet uttrykkes ved binomialkoeffisienten som
På samme måte er det n-te tetraedertallet
Summasjonsformelen for trekanttallene tilsvarer da summen
som er en kjent sammenheng mellom binomialkoeffisientene i Pascals trekant.
Induksjonsbevis for summasjonsformelen[rediger | rediger kilde]
Resultatet Tn for summen av de n første trekanttallene, kan også vises ved induksjon. Ved direkte utregning viser man at formelen er riktig for n = 2. Derfor følger det at
En indirekte konsekvens av denne summasjonsformelen er at den gir også resultatet for summen S2(n) av de n første kvadratene av de naturlige tallene. Denne summen utgjør også det n-te, kvadratiske pyramidetallet og følger fra
som gir
Her er den siste koeffisienten B2 = 1/6 definert som det andre Bernoulli-tallet. For mer enn tre hundre år siden kunne Jakob Bernoulli beregne de neste av disse viktige tallene ved å summere tetraedertallene og videre på tilsvarende vis med tallene langs de neste skrålinjene i Pascals trekant.
Formelen til Nikomakhos[rediger | rediger kilde]

På lignende måte som at summen av de n første kvadrattallene kan uttrykkes ved egenskaper til trekanttallene, kan også formelen for summen av de n første kubikktallene utledes. Betrakter man et kvadrat med høyde som er en lengdeenhet og sidelengder som er det n-te trekanttallet Δn målt i denne enheten, kan det deles opp i mindre kvadrat og halv-kvadrat. Disse kan så kombineres til n kuber med sidelengder fra 1 til n. Det betyr at
Denne berømte formelen blir vanligvis forbundet med Nikomakhos gjennom hans lærebøker i aritmetikk. Den betyr at summen
Da dette polynomet ikke inneholder et ledd som er proporsjonalt med n, betyr det ut fra definisjonen at Bernoulli-tallet B3 = 0. Bernoulli kunne ved tilsvarende betraktninger finne den generelle formelen for summen Sp(n) av vilkårlig store potenser k p av naturlige tall.
Litteratur[rediger | rediger kilde]
- A. Holme, Matematikkens Historie 1, Fagbokforlaget, Bergen (2001). ISBN 82-7674-678-0.
- J.H. Conway and R.K. Guy, The Book of Numbers, Springer-Verlag, New York (1996). ISBN 978-1-4612-8488-8.
Eksterne lenker[rediger | rediger kilde]
- AbeLie, Figurtall og Tallmønster, norske websider














