Konform avbilding

En konform avbilding gir et bilde av en flate eller metrisk rom på en tilsvarende mangfoldighet slik at vinkelen mellom to linjer som skjærer hverandre, forblir den samme. Derfor sies avbildningen å være vinkeltro. En tilstrekkelig liten figur, vil få samme form ved avbildningen og har derfor gitt opphav til betegnelsen konform. Derimot vil en endelig polygon avbildes som en ny polygon med de samme hjørnevinklene, men generelt med en ganske annen form.
I alminnelighet vil alle lengder bli forandret ved denne transformasjonen. Et lite linjeelement dσ vil få lengden ds i bildet. Matematisk er den konforme avbildningen definert ved sammenhengen
hvor skalafaktoren k(x) varierer fra punkt til punkt og er uavhengig av retningen til linjeelementet. Det betyr for eksempel at koordinatlinjene i et kartesisk koordinatsystem vil bli krumme kurver som står vinkelrett på hverandre i bildet.
Når skalafaktoren k = 1, sies avbildning å være isometrisk. Translasjoner og rotasjoner i et euklidsk rom er eksempel på slike spesielle transformasjoner. Derimot er inversjoner konforme transformasjoner med variabel skalafaktor.
Ved fremstilling av kart ønsker man ofte at avbildningen skal være konform. Både Mercator-projeksjonen og den stereografiske projeksjonen oppfyller dette kravet i motsetning til den gnomoniske projeksjonen. Likedan kan konforme transformasjoner benyttes til å løse problem innen hydrodynamikk, elektromagnetisme og andre grener innen teoretisk fysikk.
Matematisk beskrivelse[rediger | rediger kilde]
For en N-dimensjonal mangfoldighet Σ med metrisk tensor gμν og koordinater uμ kan man skrive det kvadrerte linjeelementet som
Her benyttes Einsteins summekonvensjon hvor man summer fra 1 til N over alle par med like indekser. Denne mangfoldigheten skal nå avbildes på en annen Σ' med samme dimensjon.[1] For enkelhets skyld kan man anta at dette er et euklidsk rom med koordinater xα og metrikk som kan settes lik med Kronecker-deltaet δαβ. Hvis denne avbildningen er konform, må det da finnes N deriverbare funksjoner uμ(x) mellom koordinatene på disse to mangfoldighetene slik at man har
der k(x) er en skalafaktor. Her er ds 2 = δαβ dxα dxβ = (dx1)2 + (dx 2)2 + ... + (dxN) 2 det kvadrerte linjeelement på den euklidske mangfoldigheten Σ' .
En vektor med komponenter Aμ på mangfoldigheten Σ vil avbildes på Σ' med komponenter A' μ. De er forbundet ved ligningene
som følger fra transformasjonen mellom disse to koordinatsystemene. Indreproduktet mellom to slike vektorer blir dermed
Indreproduktene mellom vektorene kan uttrykkes ved deres lengder A og B og vinkelen θ mellom dem som A⋅B = AB cosθ. Da skalafaktoren k(x) også opptrer mellom lengden A og A' før og etter transformasjonen, må cosθ = cosθ' . Avbildningen forandrer derfor ikke vinkelen mellom de to vektorene slik at den er konform.[2]
Det samme gjelder for vinkelen mellom to kurver som skjærer hverandre. Vinkelen mellom dem er da definert som vinkelen mellom deres tangentvektorer i skjæringspunktet. Denne vil på samme måte forbli uforandret ved en slik konform transformasjon.
Eksempel: Sirkelinversjon[rediger | rediger kilde]
Kanskje det eldste og mens kjente eksempel på en konform avbildning er inversjon i en sirkel.[3] Den befinner seg i et todimensjonalt plan, og man kan her sette dens radius R = 1. Hvert punkt r med koordinater (x,y) blir transformert til det inverse punktet r → r/r 2 med koordinater (u,v) hvor
Det transformerte linjeelementet er dσ 2 = du 2 + dv 2 hvor de to differensialene blir
Dermed er
slik at transformasjonen er konform. Den er derfor vinkelbevarende som man også kan bevise med rent geometriske metoder.[3]
Inversjon kan vises på samme måte å være konform når den foretas mellom to euklidske rom med dimensjon N > 2. Et geometrisk bevis er ikke enkelt i dette generelle tilfellet.[2]
Komplekse funksjoner[rediger | rediger kilde]

Konforme transformasjoner i N = 2 dimensjoner er av spesiell stor betydning. Det kommer klart frem ved å betrakte en slik transformasjon xμ → uμ(x) som involverer koordinater xμ = (x,y) og uμ = (u,v) i to euklidske plan.[1] Da er
For at dette skal være proporsjonalt med ds 2 = dx 2 + dy 2, må derfor de to funksjonene u = u(x,y) og v = v(x,y) oppfylle betingelsene
sammen med
I denne siste ligningen kan man sette ∂u /∂x = ε ∂v /∂y hvor ε er en ukjent størrelse. Den gir da at ∂v /∂x = -ε ∂u /∂y. Kombineres dette med de to første betingelsene, ser man at ε 2 = 1. Det finnes derfor uendelig mange konforme transformasjoner i to dimensjoner kun gitt ved disse to kravene til deres deriverte.[1]
Cauchy-Riemanns ligninger[rediger | rediger kilde]
Når ε = 1, er kravet for en konform avbildning at
Dette er Cauchy–Riemanns ligninger for en kompleks funksjon w(z) = u(x,y) + iv(x,y) hvor z = x + iy er den komplekse variable. Enhver slik analytisk funksjon w = f(z) gir derfor opphav til en konform avbildning i det komplekse planet. En spesielt viktig rolle har Möbius-transformasjoner som overfører linjer og sirkler på linjer og sirkler.
I det motsatte tilfelle med ε = -1 vil man på samme vis ha en konform transformasjonen hvor den kompleks konjugerte variable er . Dette er en antiholomorf transformasjon som tar en figur med en viss orientering til en tilsvarende figur med motsatt orientering. Dette skjer for eksempel ved sirkelinversjon i planet.
De to funksjonene u = u(x,y) og v = v(x,y) som gir konforme avbildninger i to dimensjoner, er harmoniske funksjoner. Det følger direkte fra Cauchy–Riemanns ligninger som gir at
Derfor oppfyller begge funksjonene Laplace-ligningen i to dimensjoner. Den opptrer også i mange forskjellige anvendelser, for eksempler innen elektrostatikken for det elektriske potensialet. Beregnes dette i et bestemt område i to dimensjoner, kan man da med en kompleks transformasjon finne det i et annet område med en forskjellig, geometrisk form.[4]
Kompleks avbildning er vinkeltro[rediger | rediger kilde]
En kurve i det komplekse planet kan generelt skrives som z(t ) = x(t ) + iy(t ) der t er dens reelle parameter. Under en kompleks transformasjon z → f(z ) vil den avbildes på en ny kurve w(t ) = f(z(t ). Dens retning er gitt ved tangentvektoren
Hvis man skriver den opprinnelige tangenten som har den en vinkel θ med x-aksen. Kalles den tilsvarende vinkelen for den transformerte tangenten for θ' , vil derfor denne være θ' = θ + ψ når man på samme vis skriver Retningen til den opprinnelige tangentvektoren blir dermed dreidd en vinkel ψ som er uavhengig av kurven og gitt ved transformasjonen alene. Skjærer to kurver derfor hverandre i et punkt z0, vil begge deres tangentvektorer dreies like mye under avbildningen. Dermed forblir vinklene mellom dem uforandret under transformasjonen.[1]
Konforme kartprojeksjoner[rediger | rediger kilde]
Mange kartprojeksjoner er konforme. Selv om slike avbildninger er vinkeltro, vil likevel deler av kartet ha mer eller mindre forvrengning da skalafaktoren eller målestokken varierer med stedet.
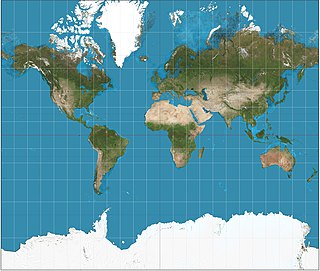
Et godt eksempel er den mye brukte Mercator-projeksjonen som avbilder en kuleflate på en sylinder som tangerer den. Settes dens radius R = 1, kan hvert punkt på sfæren angis med kulekoordinater (θ,φ) slik at den er beskrevet med metrikken
Denne kan omskrives som
etter å ha innført nye koordinater (x,y) der dx = dφ og dy = -dθ/sinθ. De kan betraktes som kartesiske koordinater på sylinderen med x = φ. Fortegnet til y-koordinaten er valgt slik at den avtar med vinkelen θ. Ved å skrive sinθ = 2sin(θ /2)cos(θ /2), finner man da ved direkte integrasjon at y = ln cot(θ /2) etter å ha bestemt integrasjonskonstanten slik at y = 0 for θ = 90°. Dette er nå en konform avbildning av kuleflaten med en skalafaktor k = sinθ som bare varierer i y-retning.[5]
Når man i et verdenskart vil ha minst forvrengning i områder på begge sider av ekvator, kan man la sylinderen tangere kuleflaten langs denne storsirkelen θ = 90°. Hvis man benytter vanlige lengdegrader λ = φ og breddegrader β = 90° - θ, vil da de kartesiske koordinatene på kartet være
Lengdegradene og breddegradene fremstilles på kartet som rette linjer som står vinkelrett på hverandre. På grunn av skalafaktoren øker forvrengningen mot polene slik at både Arktis og Antarktis synes å ha veldig stor utstrekning.
Stereografisk projeksjon[rediger | rediger kilde]

Den første kartprojeksjon ble ikke benyttet til å gi en avbildning av Jorden, men av himmelhvelvingen. Fremgangsmåten ble beskrevet allerede av Klaudius Ptolemaios i hans verk Planisphaerium. Navnet benyttes fremdeles i dag for en planisfære som er et kart over stjernehimmelen med koordinater. Den er en stereografisk projeksjon av en himmelhvelvingen på et plan med den spesielle egenskap at den er både konform og avbilder alle sirkler på sfæren som sirkler i planet.[6]
Både den gnomiske og den stereografiske projeksjonen av en kuleflate er sentralprojeksjoner fra punkt på en diameter i kulen på et plan som står vinkelrett på diameteren. Mens den første benytter kulens sentrum som projeksjonspunkt, foretas den stereografiske projeksjonen fra en av polene der diameteren møter kuleflaten. Projeksjonsplanet kan legges gjennom kulens sentrum eller som tangentplan i den motsatte polen.

Hvis man for eksempel vil avbilde områdene på den sydlige halvkule med minst forvrengning, er det naturlig å benytte Nordpolen som projeksjonspunkt og et projeksjonsplan som tangerer Sydpolen. Ved bruk av kulekoordinater (θ,φ) for et punkt P på overflaten, vil dette bli avbildet på et punkt P' med koordinater (x,y) i kartplanet hvor x = r cosφ og y = r sinφ. Her er nå r = 2 tan(θ /2) hvis man setter kulens radius R = 1 og benytter loven om periferivinkler. Derfor er hvor
Fra følger . Videre betyr at . Linjeelementet på kuleflaten transformeres dermed til
Denne delen av kuleflaten er derfor konformt ekvivalent med et euklidsk plan. Lengdegradene er radielle linjer ut fra polen, mens breddegradene er konsentriske sirkler om dette punktet. Hadde kartplanet istedet gått gjennom ekvator, ville det tilsvare forandringene x → 2x og y → 2y i metrikken. Hvis radius R til kulen hadde blitt tatt med, ville faktoren 1/4 i nevneren i stedet blitt 1/4R 2 hvor K = 1/R 2 er den gaussiske krumningen til kuleflaten.
Andre anvendelser[rediger | rediger kilde]

Konforme avbildninger kan gjøres av mangfoldigheter med dimensjoner N > 2. For eksempel kan en N-dimensjonal kuleflate eller sfærisk rom SN avbildes på et euklidsk rom EN ved en stereografisk projeksjon. Hvis dette skjer gjennom et hyperplan gjennom kulens sentrum, vil den sfæriske metrikken ta formen
på samme måte som i N = 2 dimensjoner. Her er x = (x1, x2, ... , xN) kartesiske koordinater i det euklidske rommet.
Mens det sfæriske rommet SN har konstant, positiv krumning, har det hyperbolske rommet HN konstant, negativ krumning. Det kan formelt beskrives som en kuleflate med imaginær radius. Metrikken for dette rommet kan dermed oppnås fra den sfæriske ved substitusjonen R 2 → - R 2. På den måten finner man det kvadrerte linjeelementet
Det hyperbolske rommet er derfor også konformt ekvivalent med det euklidske rommet EN og blir avbildet på innsiden av en N-dimensjonal kule.
Denne hyperbolske metrikken ble først etablert av Eugenio Beltrami som gjorde bruk av den nye differensialgeometrien til Bernhard Riemann. I N = 2 dimensjoner inneholder den viktige symmetrier som ble avdekket av Henri Poincaré. Derfor omtales også geometrien ofte som Poincarés diskmodell for det hyperbolske planet.
Penrose-diagram[rediger | rediger kilde]

Spesiell relativitetsteori kan beskrives i et 4-dimensjonalt Minkowski-rom. Når lyshastigheten settes lik med c = 1, kan det beskrives ved koordinater (t,x,y,z) eller tilsvarende kulekoordinater (t;r,θ,φ). Mange prosesser i dette rommet er uavhengige av den radielle retningen gitt ved vinklene (θ,φ) slik at linjeelementet effektivt er dσ 2 = dt 2 - dr 2. Lysstråler følger nå baner r = ± t som er rette linjer som danner 45° med aksene i det 2-dimensjonale Minkowski-rommet.
Dette uendelig store tidrom kan konformt avbildes på et endelig tidrom med koordinater (p,q) hvor
og som tar verdier i intervallet fra -π /2 til π /2. Den reduserte Minkowski-metrikken tar dermed formen
Ved å innføre konform tid T = p + q og radiell avstand R = p - q, er denne proporsjonal med ds 2 = dT 2 - dR 2 slik at hele Minkowski-rommet befinner seg innen et endelig kvadrat. En lysstråle som fulgte en bane med dσ = 0, vil etter transformasjonen følge ds = 0 som betyr at den fortsatt danner 45° med disse nye koordinataksene. Det resulterende bildet av tidrommet blir vanligvis omtalt som et Penrose-diagram etter den britiske fysiker Roger Penrose.[7]
Tidrommet rundt et sfærisk symmetrisk, sort hull kan også fremstilles i et slikt Penrose-diagram. Man benytter da Schwarzschild-løsningen av Einsteins ligninger ved bruk av Kruskal-Szekeres-koordinater. Fordelen med denne konforme fremstillingen er at den gir en bedre forståelse av geometrien og fysiske prosesser innenfor horisonten gitt ved Schwarzschild-radien.
Referanser[rediger | rediger kilde]
- ^ a b c d R. Tambs Lyche, Matematisk Analyse II, Gyldendal Norsk Forlag, Oslo (1961).
- ^ a b D.E. Blair, Inversion Theory and Conformal Mapping, Student Mathematical Library. No. 9, AMS (2000).
- ^ a b H.S.M. Coxeter and S.L. Greitzer, Geometry Revisited, Mathematical Association of America, Washington, DC (1967). ISBN 0-8838-5619-0.
- ^ R.V. Churchill, Complex Variables and Applications, McGraw–Hill, New York (1974). ISBN 978-0-07-010855-4.
- ^ E. Kreyszig, Differential Geometry, Dover Publications, New York (1991). ISBN 0-486-66721-9.
- ^ G. van Brummelen, Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry, Princeton University Press, New Jersey (2013). ISBN 978-0-691-14892-2.
- ^ C.W. Misner, K.S. Thorne and J.A. Wheeler, Gravitation, W. H. Freeman, San Francisco (1973). ISBN 0-7167-0344-0.
Eksterne lenker[rediger | rediger kilde]
- E. Weisstein, Conformal Mapping, Wolfram MathWorld









![{\displaystyle {\begin{aligned}d\sigma ^{2}&=du^{2}+dv^{2}\\&=\left[{\Big (}{\partial u \over \partial x}{\Big )}^{2}+{\Big (}{\partial v \over \partial x}{\Big )}^{2}\right]dx^{2}+\left[{\Big (}{\partial u \over \partial y}{\Big )}^{2}+{\Big (}{\partial v \over \partial y}{\Big )}^{2}\right]dy^{2}\\&+2\left({\partial u \over \partial x}{\partial u \over \partial y}+{\partial v \over \partial x}{\partial v \over \partial y}\right)dxdy\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/999207222c48f64ca22f5822a09dd20c0bd52b5f)























