Trigonometri

| Områder i geometri |
| Algebraisk geometri |
| Differensialgeometri |
| Euklidsk geometri |
| Ikke-euklidsk geometri |
|
Elliptisk geometri |
| Topologi |
| Trigonometri |
Trigonometri (fra gresk trigonon = tre vinkler, og metro = måling) er en gren innen matematikken som studerer forholdet mellom vinkler og sider i en trekant. Trigonometri anvendes i matematikk, astronomi og landmåling, men også innen felter som ikke er direkte forbundet med dette, som numerisk analyse, mekanikk og frekvensanalyse (lyd, lys, optikk, kvantemekanikk). Det er uenighet om trigonometrien er en egen matematisk gren eller om den er underlagt geometrien.
Notasjon og benevnelser[rediger | rediger kilde]
I trigonometrien blir sider og vinkler bokstavert på samme måte som ellers i geometrien.
Den lengste siden kalles hypotenusen. De andre sidene kalles for kateter. Den kateten som er spent mellom vinkelbeina til den gjeldende vinkel kalles for den motstående kateten. Den kateten som utgjør et av vinkelbeina kalles for den hosliggende kateten.
Benevnelsen på forholdene i trekanten blir forkortet. Sinus blir til sin, cosinus blir cos, og tangens blir tan. Vinkelen det gjelder for blir skrevet etter forholdet, for eksempel cos v, eller tan 38.
Når forholdet blir satt i potens skrives det med verdien av forhøyelsen til forholdet, før vinkelen, for eksempel . Hvis det feilaktig blir skrevet etter vinkelen uten paranteser kan det lett misoppfattet til at vinkelen skal i potens som i som ikke er det samme.
Forholdene i en trekant[rediger | rediger kilde]

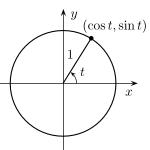
Forholdet mellom sidene og vinklene i en trekant vil alltid avhenge av hverandre, og forholdet mellom sidene kan beregnes ved hjelp av vinkelen mellom dem. Dersom lengden på den ene siden endres, vil alltid lengden på de andre sidene også endres i takt med den første siden. Så lenge vinklene er de samme, vil forholdet mellom sidene være det samme. Det er disse forholdene som danner grunnlaget for trigonometrien, og kalles sinus, cosinus og tangens. Ettersom forholdet sier noe om vinkelen, blir navnet til forholdet benevnt med hvilken vinkel det gjelder, for eksempel sin v.
- Sinus til en vinkel blir definert som forholdet mellom den motstående kateten og hypotenusen.
- Cosinus til en vinkel blir definert som forholdet mellom den hosliggende kateten og hypotenusen.
- Tangens til en vinkel blir definert som forholdet mellom den motstående kateten og den hosliggende kateten.
Utdypende artikkel: Trigonometriske funksjoner






