Sekant

En sekant er en rett linje som skjærer i gjennom en kurve i minst to punkt. Den delen av sekanten som ligger mellom to nabopunkt, er en korde. I figuren er linjen S sekanten, mens det rette linjestykket PQ er korden. Ordet sekant kommer av det latinske ordet secare som betyr å kutte eller skjære over.
Derivasjon[rediger | rediger kilde]

Sekanten kan anvendes til å finne tangenten til en kurve i et punkt. Når sekanten går gjennom de to punktene P og Q, så kommer sekanten til å nærme seg tangenten til kurven i punktet P når Q nærmer seg dette punktet langs kurven. Dette er illustrert i animasjonen til venstre.
Stigningstallet[rediger | rediger kilde]

Hellningen til sekanten er dens stigningstall. Dette kan beregnes når kurven er definert ved en funksjon y = f(x) i et kartesisk koordinatsystem. Har punktet P koordinatene (x, f(x)) og punktet Q koordinatene (x + h, f(x + h)), blir stigningstallet for sekanten gjennom disse to punktene
I grensen hvor h → 0, vil sekanten nærme seg tangenten i punktet (x, f(x)) slik at dette stigningstallet blir lik den deriverte av funksjonen y = f(x) i dette punktet. Både i analytiske og numeriske arbeider blir denne metoden benyttet til å utføre derivasjoner.
Sirkelsekanter[rediger | rediger kilde]


For en sirkel vil en sekant gi maksimalt to skjæringspunkt. Faller de sammen, går sekanten over til å bli en tangent. Den tilsvarende korden har størst lengde når sekanten går gjennom sirkelens sentrum. Korden er da en diameter i sirkelen.
To sekanter kan skjære en sirkel i maksimalt fire punkter. Disse bestemmer vinkelen ψ mellom de to sekantene. Ligger skjæringspunktet S inni sirkelen, er skjæringsvinkelen
hvor vinklene θ1 og θ2 er de to sirkelbuene som ligger mellom sekantene. Dette sees ved å trekke korden BC i figuren til høyre. Vinkel DBC er da en periferivinkel. Den har derfor en størrelse som er lik halvparten av sirkelbuen DC, det vil si θ2/2 . På samme måte er periferivinklen BCA lik halvparten av sirkelbuen AB, det vil si θ1/2 . Da nå skjæringsvinklen ψ er en utvendig vinkel i trekanten SBC, vil den være lik summen av periferivinklene DBC og BCA. Herav følger resultatet.
Hvis derimot skjæringspunktet S mellom sekantene ligger utenfor sirkelen som i den nederste figuren, vil skjæringsvinkelen ψ mellom dem være gitt som
Dette kan vises ved å trekke korden BD. Da er periferivinkelen BDA en utvendig vinkel i trekanten SBD og derfor lik skjæringsvinkelen pluss periferivinkelen DBS. Uttrykt ved gradtallene til vinklene, betyr det at θ2/2 + ψ = θ1/2 som er resultatet.
Potensen til skjæringspunktet[rediger | rediger kilde]
Mens sirkelbuene mellom sekantenes skjæringspunkt med sirkelen bestemmer vinkelen mellom dem, er produktet av de to linjestykkestykkene mellom S og hvert av de to skjæringspunktene det samme for alle sekanter gjennom S som skjærer sirkelen. Hvis S ligger innenfor sirkelen, er for eksempel SA⋅SC = SB⋅SD og med samme verdi for alle andre sekanter gjennom S. Når dette punktet ligger utenfor sirkelen, er på tilsvarende måte SA⋅SD = SB⋅SC. Man kan forklare dette ved å benytte egenskapene til periferivinkelene og de trekantene hvor de inngår.
Dette konstante produktet kalles potensen til punktet S og var kjent allerede på Euklids tid. På 1800-tallet ble det utdypet nærmere av den sveitsiske matematiker Jakob Steiner.
Elliptiske kurver[rediger | rediger kilde]
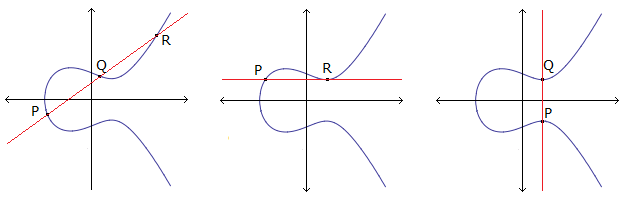
En sekant som skjærer gjennom en elliptisk kurve, vil ha maksimalt tre skjæringspunkt. Det skyldes at den er beskrevet ved en ligning av formen y2 = P(x) hvor polynomet P(x) er av tredje grad. For noen sekanter kan det også bare opptre to skjæringspunkt, for eksempel når den er tangerer kurven i et punkt.
Elliptiske kurver er viktig i tallteori og har i de senere årene fått stor, praktisk betydning i forbindelse med kryptering. Det er mulig da punktene på kurven kan adderes på en slik måte at det vil være umulig å finne ut av for en utenforstående. En sekant vil i alminnelighet ha tre skjæringspunktet P, Q og R med kurven. Summen P + Q kan nå defineres ut fra kjennskap til det tredje tallet R. Denne addisjonsloven betyr at P + Q = Q + P slik at resultatet er uavhengig av rekkefølgen til de to tallene. Den definerer derfor en abelsk gruppe med et identitetselement som tilsvarer punktet i det uendelig fjerne. Disse beregningene kan utføres i datamaskiner som benyttes i moderne datanettverk.
Litteratur[rediger | rediger kilde]
- A. Søgaard og R. Tambs Lyche, Matematikk for den høgre skolen, vol II, Gyldendal Norsk Forlag, Oslo (1955).
- A. Ash and R. Gross, Elliptic Tales, Princeton University Press, New Jersey (2012). ISBN 978-0-691-15119-9.



