Elektrisk resistans

Elektrisk resistans eller elektrisk motstand er et fysisk fenomen som uttrykker at det koster energi å transportere elektriske ladninger. Tallverdien for resistansen i en leder er definert som forholdet mellom den elektriske spenningen, målt i Volt, som ligger over lederen og den elektriske strømmen, målt i Ampere, som går gjennom den. Denne tallverdien er høyere jo mer energi det koster å transportere en gitt ladning per tidsenhet gjennom lederen, for eksempel et gitt antall elektroner per sekund. Ladning per tidsenehet er det samme som elektrisk strøm.
Formelsymbolet for resistans er R og SI-enheten er (Ohm). For metalliske ledere og for komponenten motstand (resistor) er dette forholdet en konstant, uavhengig av spenningens verdi. Men ved økende temperatur vil motstandsverdien oftest vanligvis bli litt større.
Fundamentale formler[rediger | rediger kilde]
Per definisjon er motstandsverdien R gitt av:
- hvor
- R er komponentens motstandsverdi i Ohm, []
- U er spenningen over komponenten i Volt [V]
- I er strømmen gjennom komponenten i Ampere [A]
Der verdien R for en komponent er en konstant for alle rimelige verdier av U, og når komponentens temperatur holdes konstant, kalles komponenten lineær eller Ohmsk, og den følger da Ohms lov.
Den inverse størrelsen til resistans kalles ledningsevne eller konduktans og er gitt av
G måles i Siemens (S), men betegnelsen Mho er også i bruk, særlig i USA.
For mange ledere endrer verdien av R seg med det påtrykte spenningen U. Resulterende strøm I er da ikke proporsjonal med U. Slike ledere kalles ulinjære og de følger da ikke Ohms lov.
I et spenning-strøm-diagram med spenning som X-akse og strøm som Y-akse, representeres en linjær resistans av en rett linje som går gjennom origo. Et gitt spenningspåtrykk representeres som et punkt på denne linjen. En lav R-verdi som en kortslutning ses som en vertikal linje og en svært stor motstandsverdi, som i en isolator, ses som en horisontal linje. Der linjen er krum, er lederen ulinjær og hvis den ikke går gjennom origo kan komponenten levere energi. Enhver motstand må ligge plassert i en av de to kvadrantene som har samme fortegn for strøm og spenning, altså i kvadrantene 1 og 3. I disse kvadrantene forbrukes energi, som blir til varme. I de to andre kvadrantene avgir komponenten energi og er således ikke en motstand, og en teoretisk motstandsverdi ville da være negativ.

Resistivitet[rediger | rediger kilde]
Utdypende artikkel: Resistivitet
Resistivitet (spesifikk motstand eller spesifikk resistans) er en materialegenskap. Denne er av betydning for for materialer som skal lede elektrisk strøm, som kraftledninger og motstander. Vanlig symbol for resistivitet er ρ, SI-enhet er Ohm-meter (Ωm). Resistivitet er definert som resistansen i et materialstykke med lengde 1 meter og tverrsnitt 1 m². Motstanden i lederen er gitt av
hvor
- er stykkets resistans i Ohm
- er stykkets lengde i meter
- er stykkets areal (tverrsnitt) i kvadratmeter
Temperaturavhengighet[rediger | rediger kilde]
Temperaturen har som regel innflytelse på resitiviteten. Motstandsverdien øker med stigende temperatur for de aller fleste stoffer. 20 grader celsius blir oftest brukt som referansetemperatur ved spesifikasjon av resitivitetens verdi. Matematisk beskrives resistansen som funksjon av temperaturen i et førsteordens system som:
hvor T er temperaturen målt i grader celsius og er første ordens temperaturkoeffisient (TCR) med dimensjonen "per grad" eller (°C)-1. kan være positiv eller negativ. Det finnes naturligvis stoffer som er utviklet for å ha ekstreme temperaturkoeffisienter. Komponenter laget av disse stoffene kan gruppere som
- NTC-motstander (Negative temperature Coefficient), eller varmledere, er sterkt negativ.
- PTC-motstander (Positive temperature Coefficient), eller kaldledere, er sterkt positiv
I slike motstander er verdien av oftest ikke linjær, varierer altså med temperaturen.
I tillegg finnes legeringer som oppviser nesten ingen temperaturavhengighet i motstanden. Et eksempel på en slik legering er konstantan. Konstantan er en legering av omtrent 55 % kopper og 45 % nikkel, av og til med noe mangan. Sammensetningen kan variere noe. Cirkaverdier er
Kanthal er en FeCrAl-legering med liten temperaturkoeffisient.
Det første forsøk på å gi en mikroskopisk forklaring av elektrisk motstand ble gitt i Drude-modellen rundt 1900 like etter at elektronet var oppdaget. Den inneholder også en enkel forklaring på hvorfor motstanden øker med temperaturen.
Strekkavhengighet[rediger | rediger kilde]

En strekking eller en sammenstuing av en leder vil deformere den noe, siden alle materialer er elastiske. Deformasjonen fører til en endring av resistansen. For eksempel ved strekking av en kabel vil den bli både lengre og tynnere, og begge deler fører til øket resistans.
Denne effekten utnyttes i strekk-sensorer (engelsk: strain gauges), som består av en isolerende flate med flere parallelle, seriekoplede ledere. Sensoren limes fast til den mekaniske delen som skal undersøkes. Siden endringene i resistansen er ganske små, blir sensoren ofte satt inn som en av fire like store resistanser i en balansert wheatstone-bro for å øke målingens sensitivitet. De tre andre bro-grenene har da faste resistanser.
Som del av impedans[rediger | rediger kilde]
Impedans er et begrep som bare har gyldighet for vekselspenninger og -strømmer. Resistansen kalles den såkalt reelle delen av en impedans. Den andre delen er reaktansen, som kan være kapasitiv eller induktiv. Resistansen er den delen av impedansen som forbruker energi (omdanner den til varme). Reaktansene opptar, lagrer og avgir energi i løpet av en periode, men kan ikke forbruke den. For en impedans er strømmen gjennom den og spenningen over den ikke i fase, men forskjellen er begrenset til +/- 90 grader.
Vekselstrøm[rediger | rediger kilde]
Resistansen er like mye gyldig for likestrøm som for vekselstrøm. Man kan snakke om motstand for spoler og kondensatorer, og mener da deres impedans.
Resistansen til en metallisk leder vil øke ved høye frekvenser, siden strømledningen inne i lederen reduseres da strømmen tvinges ut mot overflaten. Effekten kalles 'skin effect' på engelsk, som betyr hud- eller overflate-effekt. Av denne grunn blir høyfrekvensspoler ofte viklet av forsølvet koppertråd, eller av tynne sølvbånd.
I tillegg kommer 'proximity effect', da strømledere påvirker hverandre når de fører vekselstrøm. I en fram- og tilbakeleder som ligger nært, vil strømmen prøve å komme så nært som mulig den andre lederen. Dette gir også høyere resistans.
Spenningstap i linjeresistans[rediger | rediger kilde]
Elektriske ledere som brukes til energitransport over avstander kalles kraftlinjer. Slike linjer oppviser en motstand som fører til at en del av energien tapes på veien fordi spenningen reduseres noe på veien. Dette følger av innledningens observasjon: det koster energi å transportere ladninger. Differansen mellom spenningsverdien ved kilden og verdien ved forbrukeren kalles spenningstapet til linjen. Strømmen er lik på begge sider.
Både effekttapet og spenningstapet varierer med mengden av energi som transporteres; større transportert energi fører til større tap.
Sett nøyere er det strømmen gjennom linjen som fører til tap. Spenningstapet på veien øker lineært med strømmen som
der spenningstapet er UT, linjeresistansen er RL, og strømmen er: IL
Effekttapet beregnes som UT*IL og blir
Effekttapet er derfor proporsjonalt med strømmen i kvadrat, og er uavhengig av linjespenningen. For å redusere transporttapene reduseres derfor strømmen. For samme mengde transportert energi må da spenningen over linjen økes tilsvarende for at verdien P=U*I skal være konstant; U er her linjespenningen. Derfor brukes høyspenning for å redusere strømmen der det er snakk om mye energi og lange strekninger. Spenningen reduseres så i en transformatorstasjon lokalt før den gis videre til forbrukerne. Den lokale spenningen 220-240 V er gitt som et kompromiss mellom høyest mulig spenning og dens farlighetsgrad for mennesker. Land som bruker 110-120 V er mere konservative her.
I prinsipp er det ikke noe annerledes ved bruk av vekselstrøm eller trefase; beskrivelser og beregninger blir bare noe mer komplisert.
En kraftlinje har forøvrig ikke bare resistans; både induktiviteter og kapasiteter langs linjen har innflytelse på linjens oppførsel.
Flateresistans[rediger | rediger kilde]
En isolerende flate dekket av et jevnt ledende sjikt danner en flateresistans. Dens motstandsverdi oppgis som Ohm per kvadrat siden ethvert kvadrat uansett størrelse oppviser den samme motstandsverdien fra kant til kant.
Dette er gitt av et kvadrat med doblet sidelengde kan betraktes som en parallellkopling av to seriekoplinger.
Negativ differensiell resistans[rediger | rediger kilde]
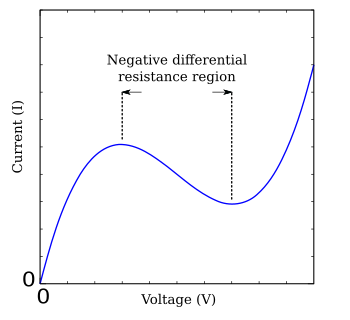
En negativ resistans kan ikke finnes som passiv komponent siden den ville avgi energi. Det finnes imidlertid spesielle komponenter som reduserer strømtrekket når de får tilført mere spenning. Dette fenomenet kalles negativ differensiell resistans og kan bare opptre i en begrenset del av karakteristikken. I hele området gjelder likevel at resistansen som absoluttverdi er positiv. Tetroder kan ha små (uønskede) områder med negativ differensiell resistans, og tunnelldioder er laget med dette som formål. De kan fungere som enkle oscillatorer sammen med reaktive komponenter og en forsyningsspenning. Andre komponenter eller fenomen med denne egenskapen er elektriske lysbuer, lysstoffrør, IMPATT- og Gunn-dioder, unijunction-transistorer og flere.
Serie- og parallellkopling av to resistanser[rediger | rediger kilde]
Når to resistanser koples i serie deler de strømmen og får hver sin spenning slik at
Når resistanser parallellkoples deler de spenningen og får hver sin strøm slik at ledningsevnene kan adderes.
eller uttrykt med R:
Denne formelen illustreres best ved den geometriske Arbelos-figuren der den inneholder Archimedes' dobbeltsirkler. Parallellmotstanden er diameteren på hver av de øvre, like store, dobbeltsirklene, hvor de to innskrevne enkeltsirklenes diametre (som deler storsirkelens diameter i to deler) er de enkelte motstandsverdier. Seriekoplingen er selvfølgelig summen av de to, storsirkelens diameter. Arbelos (Nettstedet bruker Java. Nyere versjoner av Java vil forby kjøring av scripts som er ukjente, av sikkerhetsgrunner. For å legge inn tillatelse, i Windows, klikk Start, Alle programmer, åpne Java-mappen, klikk på Configure-delen, velg Security-tab, edit Site list, "add", og føy til URL-en http://www.retas.de.)
Denne formelen kan også brukes til parallellkopling:
Fordelen med denne er at man enkelt kan putte inn flere enn to resistanser.
Transformasjoner[rediger | rediger kilde]


Når det skal beregnes forhold i nettverk kan det fort komme til problemer med å sette opp passende ligninger. Et godt kjent eksempel er beregninger i en ubalansert wheatstone-bro. For å kunne forenkle nettverksdiagrammene kan en ty til transformasjon av tre motstander fra en konfigurasjon til en annen. Konfigurasjonene kalles stjerne og trekant (eng. star og delta).
En stjerne har tre motstander utgående fra et felles sentrum.
En trekant har tre motstander plassert i et triangel.
Disse konfigurasjonene er fullstendig likeverdige hvis motstandsverdiene deres er riktig tilpasset.
Transformasjon fra trekant til stjerne er enklest.
Nevneren er alltid den samme, telleren består av de to hosliggende resistansene for det samme punktet.
Fra stjerne til trekant kan en bruke samme formelen hvis en bruker ledningsevnene i stedet for motstandsverdiene og de to bakenforliggende motstandene.
Ellers er formelen for stjerne-trekant motstandsberegning:
hvor er den bortliggende resistansen. Her er telleren alltid lik.
Formlene må brukes en gang per motstand, altså tilsammen tre ganger. Formlene sier ikke noe om hvor mye effekt hver transformerte motstand må tåle.
Det viktigste er at stjernen oppfører seg nøyaktig likt som trekanten. Slik kan de fem wheatstone-motstandene reduseres til tre idet en får to enkle seriekoplinger som hver slås sammen til en motstand.
Effektforbruket[rediger | rediger kilde]
Produktet av spenningen over og strømmen gjennom motstanden sier oss hvor mye effekt som tilføres motstanden.
Denne effekten omgjøres til varme i motstanden.
Effekten P fås av
som kan omskrives for variasjon av spenningen til
eller til variasjon av strømmen som
Superledning[rediger | rediger kilde]
Ved superledning ledes strømmen helt uten motstand. Den spesifikke motstanden er null ved superledning.
Superledning er kun blitt påvist ved svært lave temperaturer, lavere enn -150 grader Celcius (123 grader Kelvin). Metaller blir superledende først under ca. 4 grader Kelvin.
Støy[rediger | rediger kilde]
Motstander er kilde til såkalt elektrisk støy. Denne støyen er et elektrisk signal som motstanden gir fra seg på grunn av elektronenes termiske bevegelser i motstandsmaterialet, og som er uavhengig av strømmen. Bevegelsene er i mengde proporsjonal med den absolutte temperaturen, altså temperaturen målt i grader Kelvin, derfor er også den potensielle støyenergien proporsjonal med denne temperaturen.
Støyspenningnen over en ubelastet motstand beskrives av formelen
der
vn er rms-verdien av støyspenningen over motstanden. For betydningen av betegnelsen rms, se voltmeter.
kB er Boltzmanns konstant
T er temperaturen i grad K, Kelvin
R er motstandsverdien i Ω, Ohm
Δf er båndbredden som betraktes, i Hz
Beregningsmessig er støyen å betrakte som en spennings-støykilde som er koplet i serie med en ideell motstand. En kortsluttet motstand vil derfor føre til en støystrøm gjennom den som er lik in = vn/R.
Eksempelvis vil en motstand med verdien 10 kΩ avgi et signal med en rms-verdi for støyspenningen lik 1.8 μV når bandbredden er 20 kHz.
Denne støyen kalles på norsk hovedsakelig termisk støy, men på engelsk brukes thermal noise, Johnson noise, Nyquist noise, eller Johnson-Nyquist noise og den er spektralt sett en hvit støy.
Se også[rediger | rediger kilde]
Litteratur[rediger | rediger kilde]
- Horowitz and Hill: The art of electronics, Cambridge University Press, England (1990). ISBN 0-521-37095-7
- M.A. Omar, Elementary Solid State Physics, Addison-Wesley Publishing Company, Reading Massachusetts (1975). ISBN 0-201-05482-5.


























