Spesifikk relativ drivmoment
Det spesifikke relative drivmomentet spiller en viktig rolle i himmelmekanikk for å løse tolegemeproblemet. Man kan vise at vektoren er konstant for en gitt bane under ideale forhold, noe som beviser Keplers andre lov.
Navnet spesifikk drivmoment kommer fra at man ikke ser på det egentlige drivmomentet , men på drivmomentet per masse
Det betyr at SI-enhet er: m2·s−1. betegner her den reduserte massen .
Kraver[rediger | rediger kilde]
Det som følger trenger noen forenklende kraver som også gjelder for Newtons gravitasjonsteori.
Man ser på to punktformede masser og som er i avstand fra hverandre. Tyngdekraften virker uten forsinkelse og over hvilken som helst distanse og er den eneste kraften. Koordinatsystemet er inersial.
Nå antar man at . Det betyr at er sentrallegemet i origo, og at er satellitten som går rundt den. Den reduserte massen er nå lik og tolegemeproblemets ligning er
med gravitasjonsparameteren og avstandsvektor (lengden er ) som peker fra origo (sentrallegemet) til satellitten fordi .[Fotnoter 1]
Det er viktig å ikke forveksle gravitasjonsparameteren med den reduserte massen som blir ofte betegnet med den samme bokstaven .
Spesifikk relativ drivmoment[rediger | rediger kilde]

Man får det spesifikke drivmomentet når man multipliserer (kryssprodukt) tolegemeproblemets ligning med avstandsvektoren
Kryssproduktet av en vektor med seg selv (høyre side) er 0. Den venstre siden forenkler seg slik
ifølge produktregelen i derivasjon.
Der betyr at er konstant (blir bevart). Og dette er akkurat satellittens drivmoment per masse [Referanser 1]
Vektoren står vinkelrett på banen. Den forblir pa det samme plan fordi drivmomentet er konstant.
Med definisjonen av "Flight Path Angle" og de transversale og radiale komponentene til hastighetsvektoren (se på bildet til høyre) får man noen viktig kunnskap om tolegemetproblemet. De neste tre ligningene er alle mulige former for å angi lengden til drivmomentvektoren
Keplers lover[rediger | rediger kilde]
Utdypende artikkel: Keplers lover
Med dem som ble funnet ut i det forrige avsnittet kan man bevise Keplers lover nesten direkte.
Keplers første lov[rediger | rediger kilde]
Beviseet begynner igjen med tolegemetproblemets ligning. Denne gangen multipliserer (kryssprodukt) man med det spesifikke relative drivmomentet
Den venstre siden er lik derivasjonen fordi drivmomentet er konstant.
Den høyre siden kan omskrives slik etter flere trinn
Hvis man setter begge lik og integrerer over tiden får man med integrasjonskonstanten
Nå multipliserer man dette (skalarprodukt) med
Til slutt følger ligningen til Omløpsbanen Schließlich erhält man die Bahngleichung [Referanser 2]
som beskriver et kjeglesnitt i polare koordinater med semi latus rectum og eksentrisiteten . Derved er Keplers første lov beviset som er i ord:
Planetene beveger seg i ellipser med Solen i det ene brennpunktet.
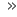
Keplers andre lov[rediger | rediger kilde]
Den andre av de tre ligningene for å angi lengden til drivmomentvektoren fører direkte til Keplers andre lov.
Forbinder man nemlig denne formen av ligningen med arealet av en sektor med en infinitesimal liten vinkel (altså arealet til en trekant med en veldig liten side), følger [Referanser 4]
som er ligningen til loven:
En rett linje fra Solen til planeten, radiusvektor, beskriver like store flater i like lange tidsrom.
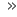
Keplers tredje lov[rediger | rediger kilde]
Den tredje loven får man ut av den andre loven. Integrasjon over et omløp gir omløpstiden
for arealet til en ellipse. Hvis man skriver for den liten halvaksen og for det spesifikke relative drivmomentet blir ligningen til [Referanser 4]
Det er altså en sammenheng mellom den store halvaksen og omløpstiden til en satellitt som er bare avhengig av en konstant til sentrallegemet. Det er det samme som Keplers formulering av loven:
Kvadratet av den sideriske omløpstid for en planet er proporsjonalt med 3. potens av dens midlere avstand fra Solen.
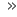
Se også[rediger | rediger kilde]
- Spesifikk baneenergi, en annen størrelse som bevares i tolegemeproblemet.
Fotnoter[rediger | rediger kilde]
- ^ Man må ikke anta dette for å utlede det spesifikke relative drivmomentet. Uten det er gravitasjonsparameteren , forblir den reduserte massen (ikke ) og origo ligger i Massesentrumet. Men forenklingen er nesten alltid god og det blir enklere og bevise Keplers lover.
Referanser[rediger | rediger kilde]
- ^ David A. Vallado (2013). Fundamentals of Astrodynamics and Applications (engelsk). Hawthorne, CA: Micorcosm Press. s. 24. ISBN 9781881883180.
- ^ David A. Vallado (2013). Fundamentals of Astrodynamics and Applications (engelsk). Hawthorne, CA: Micorcosm Press. s. 28. ISBN 9781881883180.
- ^ a b c «Keplers lover – Store norske leksikon». Store norske leksikon. Besøkt 7. juni 2016.
- ^ a b David A. Vallado (2013). Fundamentals of Astrodynamics and Applications (engelsk). Hawthorne, CA: Micorcosm Press. s. 30. ISBN 9781881883180.











































