Polarkoordinatsystem

To punkter med tilhørende koordinatsett angitt med polarkoordinater

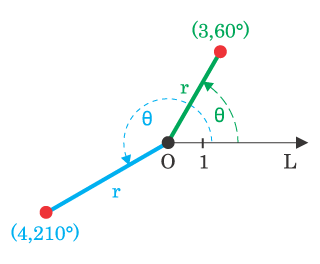
Et polarkoordinatsystem er et koordinatsystem hvor hvert punkt i et plan er bestemt ut ifra avstanden fra et gitt punkt (vanligvis origo) og vinkel i forhold til X-aksen. I et vanlig kartesisk koordinatsystem blir punktene bestemt ut ifra avstanden til hver koordinatakse.

Prinsippet i polarkoordinater er at man angir alle punkter ved hjelp av følgende informasjon:

• Punktets vinkel (grader eller radianer ) i forhold til hva man ville kalle x-aksen i et rektangulært koordinatsystem, θ.
• Punktets avstand fra origo, r.

Konvertering mellom polare og kartesiske koordinater

Et diagram som viser forholdet mellom polare og karteiske koordinater.

Omregning polarkoordinater til kartesiske koordinater kan gjøres ved:

$x = r \cos \theta \,$

$y = r \sin \theta, \,$

Mens omregningen fra karteiske koordinater til poolarkordinater kan gjøres ved:

$r = \sqrt{y^2 + x^2} \quad$ (Gitt ved Pythagoras’ læresetning), og

$\theta = \begin{cases} 0 & \mbox{hvis } x = 0 \mbox{ og } y = 0\\ \arcsin(\frac{y}{r}) & \mbox{hvis } x \geq 0 \\ \arcsin(\frac{y}{r}) + \pi & \mbox{hvis } x < 0\\ \end{cases}$

Alle disse formlene forutsetter at referansepunktet for polarkoordinatsystemet er origo. Arcsinfunksjonen er den inverse funksjonen til sinusfunksjonen og gir en løsning i intervallet [−π/2,+π/2], så formelen for θ vil gi en løsning i intervallet [−π/2,+π/2]. Dersom man vil finne θ i intervallet [0, 2π) kan man også bruke:

$\theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{hvis } x > 0 \mbox{ og } y \ge 0\\ \arctan(\frac{y}{x}) + 2\pi & \mbox{hvis } x > 0 \mbox{ og } y < 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{hvis } x < 0\\ \frac{\pi}{2} & \mbox{hvis } x = 0 \mbox{ og } y > 0\\ \frac{3\pi}{2} & \mbox{hvis } x = 0 \mbox{ og } y < 0\\ 0 & \mbox{hvis } x = 0 \mbox{ og } y = 0 \end{cases}$

Anvendelse av polarkoordinater

En sirkel

En ligning uttrykt i polarkoordinater er kjent som en polar ligning. Normalt er disse ligningene gitt ved å definere r som en funksjon av θ. Denne definisjonen gir visse fordeler i anvendelsen av polarkoordinater i forhold til hva man kan oppnå med rektangulære. Særlig fordelagtig er det å bruke polarkoordinater hvor det inngår noe sirkulært. Det enklest tenkelige eksempel er å fremstille en sirkel. Her er definisjonen av en sirkel med radius 1.

$\left. \begin{matrix} x = r \cdot \cos(\varphi)\\ y = r \cdot \sin(\varphi) \end{matrix} \right\} \quad , r = 1 \quad , \quad \varphi \in [0 , 2\pi]$

Lengden til det bevegelige punktet, settes altså konstant til å være lik én, som altså er avstanden fra origo til periferien. Deretter settes vinkelen til å variere mellem 0 og 2π eksklusiv (eller 0 og 360° i vinkler), hvor hele sirklen er med.

Arkimedisk spiral

En arm av en arkimedisk spiral ligningen r(θ) = θ for 0 < θ < 6π

En arkimedisk spiral er en spiral som ble oppdaget av Arkimedes, som kan forklares med polarkoordinater. Spiralen har formelen

$r(\theta) = a+b\theta. \,$

Ved å forandre a vil spiralen skifte form, mens b er distanseen mellom kurvene, som for en gitt spiral alltid er konstant. Den Arkimediske spiralen har to kurver, en for θ > 0 og en for θ < 0. De to kurvene starter i origo. Sett bort fra kjeglesnittene var denne kurven blandt de første til å bli beskrevet. Kurven er også et godt eksempel på kurver som blir best beskrevet med polarkoordinater.

Polar rose

En polar rose med ligning: r(θ) = 2 sin 4θ

En polar rose er en matematisk kurve som ser ut som en blomst med kronblader, denne kan defineres som en enkel polar ligning.

$r(\theta) = a \cos (k\theta + \phi_0)\,$

For enhver konstant $\phi_0$ (Inkludert 0). Dersom k er et heltall vil disse ligningene gi kurver hvor «blomsten» har k kronblader når k er et oddetall og 2k kronblader når k er et partall. Dersom k er et rasjonalt tall, men ikke et heltall vil man også få frem en blomst hvor kronbladene overlapper hverandre. Her må imidlertid definisjonsintervallet for kurven være større enn [0, 2π) for at «blomsten» skal bli komplett. Merk at det er umulig å definere en kurve hvor man får $4n +2$, hvor n er et heltall, kronblader. Variabelen a angir lengden på kronbladene.

Kjeglesnitt

Alle kjeglesnittene kan også uttrykkes ved hjelp av polarkoordinater gjennom formelen:

$r = { \ell\over {1 + e \cos \theta}}$

Hvor e er eksentrisiteten. og $\ell$ er semi latus rectum

Derson e > 1, vil ligningen gi en hyperbel; e = 1 gir en parabel mens e < 1 gir oss en ellipse. Spesialtilfellet e = 0 vil gi en sirkel mad radius $\ell$.

Anvendelse i tre dimensjoner

Polarkoordinater kan også anvendes til bruk i tre dimensjoner. Kulekoordinater og sylinderkoordinater inneholder begge polarkoordinatplanet, utvidet med en ekstra akse.

Sylinderkoordinater

Punktet P plottet med sylinderkoordinater

Sylinderkoordinater systemet er en utvidelse av polarkoordinater med en ekstra z-akse, på samme måte som det kartesiske koordinatsytemet i tre dimensjoner. Den tredje koordinaten er vanligvis uttrykt med en h eller en z, som beskriver høyden til det øvre planet i sylinderen. Alle tre koordinatene blir da skrevet (r, θ, h).

Sammenhengen mellom de tre sylinderkoordinatene og de respektive kartesiske koordinatene blir

$\begin{align} x &= r \, \cos\theta \\ y &= r \, \sin\theta \\ z &= h. \end{align}$

Kulekoordinater

Punktet P plottet med s kulekoordinat systemet

Kulekoordinatsystemet er et koordinatsystem basert på polarkoordinater. Kulekoordinater skiller seg fra polarkoordinater ved at høyden fra xy-planet blir beskrevet av en vinkel φ fra z-aksen, og at radien på xy-planet r er bekrevet med ρ som er radien fra origo til flaten til et legeme på et vilkårlig punkt. Vinkelen til φ varierer med en størrelsene 0°-180° eller 0-π radianer. Alle de tre koordinatene blir da skrevet (ρ, θ, φ).

Sammenhengen mellom de tre kulekoordinatene og de respektive kartesiske koordinatene blir;

$\begin{align} x &= \rho \, \sin\varphi \, \cos\theta \\ y &= \rho \, \sin\varphi \, \sin\theta \\ z &= \rho \, \cos\varphi. \end{align}$