Fermats prinsipp
Fermats prinsipp ble foreslått av den franske jurist og matematiker Pierre de Fermat (1601 - 1665) rundt 1660 for lysets bevegelse. I utgangspunktet sier prinsippet sier at en lysstråle som beveger seg fra et punkt til et annet, velger den veien som leder raskest frem til målet. I den følgende tid ble tilsvarende prinsipp for mekaniske system funnet av den franske naturviter Pierre Louis Maupertuis (1698 - 1759) og den irske matematiker William Rowan Hamilton (1805 - 1865). Disse virkningsprinsippene danner i dag grunnlaget for all moderne fysikk og fikk først en dypere forklaring med kvantemekanikken. Spesielt har den amerikanske fysiker Richard Feynman (1918 - 1988) bidratt til dette.
Hastigheten c til lys som går gjennom et medium, er mindre enn lyshastigheten c0 i vakuum. Matematisk uttrykkes dette som c = c0 /n hvor n > 1 er brytningsindeksen til mediet. Den kan variere med posisjonen r i mediet slik at man i alminnelighet har n = n (r). Lyset behøver derfor en tid dt = ds/c = n ds/c0 for å tilbakelegge en liten veilengde ds. Går lyset langs en bestemt bane fra et punkt A til et punkt B, trenger det da en endelig tid T = L/c0 hvor
er den optiske veilengden. Denne beskrivelsen er gyldig når bølgelengden til lyset er mye mindre enn karakteristiske lengder i systemet man beskriver. Man kan da benytte denne form for geometrisk optikk.
Fermats prinsipp sier at lyset velger den banen som gir den minste tiden T. Mer generelt sier det at denne tiden skal være ekstremal, det vil si enten være minimal eller noen ganger også maksimal. Det ekvivalent med å si at denne skal være stasjonær under små forandringer. En liten variasjon av banen skal gi en forsvinnende liten variasjon av den optiske veilengden. Matematisk skrives dette som
Den fysiske banen kan nå beregnes ved bruk av variasjonsregning som for andre virkningsprinsipp.
Refleksjon[rediger | rediger kilde]

Fermat foreslo dette nye prinsippet for å forklaring Snells brytningslov for avbøyning av lys når det går fra et medium til et annet. Den franske filosof og matematiker Descartes hadde tidligere forsøkt å gi en mekanisk utledning av denne loven. Men han måtte da anta at lyset beveget seg raskere i et tett medium som vann enn i et tynnere medium som luft. Dette fant Fermat vanskelig å akseptere, delvis kanskje fordi at det strider mot vanlig intuisjon.[1]
I stedet baserte han sin tenkning på bevegelsen av en lysstråle under refleksjon mot grenseflaten til et annet medium. Allerede fra antikken var det kjent at da vil innfallsvinkel θ være like stor som utfallsvinkelen θ', begge målt mot normalen til grenseflaten. Går lyset fra punkt A til punkt B, er det ekvivalent med at den tilbakelagte strekningen APB er minst mulig. Det er lett å se ved å betrakte det reflekterte punktet B'. Da linjestykket PB = PB', er også veien APB = APB'. Og linjen APB' mellom A og B' er kortest mulig når den er en rett linje. Kun da vil vinklene θ = θ' som sees direkte ut av figuren for det tilfellet.
Denne refleksjonsloven kan nå vises å være en konsekvens av Fermats prinsipp. La punktet A ligge på y-aksen i avstand y1 fra x-aksen, mens punkt A har koordinatene (x2, y2). For et vilkårlig punkt P på x aksen blir da den optiske lengden mellom A og B
For at denne skal ha et minimum, må den deriverte med hensyn på koordinaten x til punktet P være null. Det gir
Fra figuren ser man nå at det første leddet er sinθ, mens det andre leddet er sinθ' . Fermats prinsipp gir derfor
som er akkurat det forventete resultatet. I mer kompliserte situasjoner med refleksjon fra krumme flater gjør tilsvarende beregninger også det mulig å beregne lysets gang.[2]
Snells brytningslov[rediger | rediger kilde]

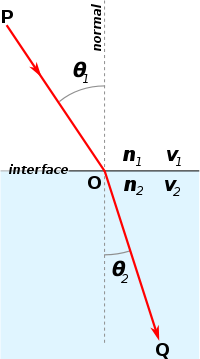
Når lyset går fra et medium 1 til et annet medium 2, vil det i alminnelighet avbøyes. I enkleste tilfelle kan man tenke seg de to medier adskilt med en plan grenseflate som vist i figuren. Den optiske avstanden langs en vei fra A til B er da
hvor x er koordinaten for et vilkårlig punkt P langs x-aksen hvor lysstrålen treffer grenseflaten, og n1 og n2 er brytningsindeksene i de to mediene. For at denne skal ha et minimum, må den deriverte med hensyn på x være null. Det gir
Fra figuren ser man nå at det første leddet er sinθ1, mens det andre leddet er sinθ2 . Fermats prinsipp gir derfor
som er Snells brytningslov. Hadde lyset gått den motsatte veien fra B til A, ville det opplagt ha fulgt den samme veien.
Variabel brytningsindeks[rediger | rediger kilde]
Man generelt kan man tenke seg et medium med et brytningsindeks n(r) som varierer med posisjonen r i mediet. Banen som lyset vil følge, blir da en eller annen kurve r = r(σ) hvor σ er en vilkårlig parameter. Hvis begynnelsespunktet A for banen har parameterverdi σA og tilsvarende σB for sluttpunktet B, kan den optiske veilengden for den søkte banen beregnes fra integralet
hvor den deriverte = d r/dσ. Her har man benyttet at den kvadrerte buelengden ds2 = d r⋅d r med vektornotasjon.
For å beregne en stasjonær verdi for dette integralet, kan man nå benytte standard variasjonsregning for funksjonen . Direkte derivasjon kan nå gjøres for hver komponent av den variable som her er posisjonsvektoren r for hvert punkt på den søkte banen. Resultatet kan sammenfattes på vektorform ved ligningene
- og
slik at Euler-Lagrange-funksjonen blir
På denne generelle formen er det vanskelig å si hva slags løsninger differensialligningen har og hva de sier om lysets bevegelse.[3]
Parametrisering[rediger | rediger kilde]
Fermats prinsipp gjør det mulig og bestemme banen r = r(σ) til en lysstråle. Den er en kurve i rommet, parametrisert ved σ som til nå ikke er nærmere spesifisert. Ved et fornuftig valg av denne parameteren, kan løsningen av bevegelsesligningene forenkles.
Den naturlige parametrisering for kurver er dens buelengde s. Da blir og den generelle Euler-Lagrange-ligningen forenkles til
Denne er nå mer egnet til å utlede fysiske konsekvenser for lysets utbredelse. For eksempel, i et laminært system vil brytningsindeksen bare variere i en koordinatretning. Lar vi denne være z-aksen, vil da n = n(z). Høyresiden av bevegelsesligningen gir da null både i x- og y-retning. Derfor må både ndx/ds og ndy/ds være konstante under lysets gang. Det betyr igjen at også n√(dx2 + dy2)/ds = konst. Her er faktoren som multipliserer n, sinus til vinkelen θ som lysstrålen danner med z-aksen. Resultatet er derfor
som er Snells brytningslov. Men i dette laminære tilfellet gjelder den lokalt i hvert punkt langs lysstrålen.
Optisk tid[rediger | rediger kilde]
En annen parametrisering er å velge σ slik at . Kaller vi denne parameteren for τ, blir derfor det differensielle linjeelementet ds = n dτ. Dermed opptrer denne nye parameteren som en slags tid og gjør det mulig å betrakte brytningsindeksen n som hastigheten til lyset. Selv om τ har like lite å gjøre med fysisk tid som n har med fysisk hastighet å gjøre, kan man matematisk benytte slike begrep her.[4]
Denne beskrivelsen av lysets gang, tilsvarer nå den som Descartes brukte for å forklare Snells brytningslov. Lyset har en fiktiv hastighet som er gitt ved brytningsindeksen og er derfor større i et tettere medium enn i et tynnere medium. Beveger det seg fra et tynnere medium mot en grenseflate til et tykkere medium, vil det bøyes inn mot normalen til grenseflaten.
Med denne parametriseringen forenkles nå Euler-Lagrange-ligningene til
Dette ser ut som Newtons andre lov for en partikkel som beveger seg i et potensial V = - (1/2)n2. Den vil bøyes i retning hvor potensialet avtar, det vil si hvor brytningsindeksen øker. Totalenergien til partikkelen
er konstant da brytningsindeksen ikke varierer med denne optiske tiden.
Man kan benytte denne beskrivelsen i praktiske anvendelser. For eksempel, i et optisk fiber avtar brytningsindeksen med avstanden fra sentrum. Det tilsvarer at det ekvivalente potensialet V øker utover i fiberet og kan dermed holde lysstrålen på plass.
Paraksial approksimasjon[rediger | rediger kilde]
For et optisk system hvor lyset i hovedsak beveger seg i z-retning med mindre avvik i x- og y-retningene, er det naturlig å bruke koordinaten z som parameter. Dermed kan lysets gang beskrives ved de to funksjoner x = x(z) og y = y(z). Da vil
hvor x' = dx/dz og y' = dy/dz angir lysstrålens retning i forhold til z-aksen. Når avviket fra denne er lite, kan man derfor med god nøyaktighet sette ds = dz. Denne forenkling omtales som den paraksiale approksimasjon.[3] Da vil lysstrålen følge en bane som er gitt ved ligningen
Den kan løses for x = x(z) og y = y(z) når retningene x' og y' er gitt på et sted med parameter z0. For z-retningen reduseres ligningen til en enkel identitet.
Laminær lysgang[rediger | rediger kilde]

I et laminært system varierer brytningsindeksen bare i en retning, det vil si at den avhenger bare av en koordinat. Lyset vil da kun avbøyes i denne retningen som her velges å være y-aksen slik at n = n(y). De andre koordinatene velges slik at lysets bane ligger i xy-planet. Den vil dermed beskrive en kurve y = y(x) med differensielt linjeelement
hvor y' = dy/dx. Fra den optiske veilengden
mellom punktene A og B følger nå Euler-Lagrange-ligningen
Den kan noe forenkles ved å gjennomføre derivasjonene. Det gir
men likevel kan en slik andre ordens differensialligning vanskelig løses for en gitt funksjon n = n(y). I det spesielle tilfellet at denne er konstant, er løsningen for lysbanen en rett linje y' = konst som forventet.
Integranden F = n(y)√(1 + y' 2) inneholder ingen eksplisitt avhengighet av den variable x som her spiller rollen som en slags tid som parametriserer banen. Derfor følger fra variasjonsregning at størrelsen K = F - pyy' , hvor py er den konjugerte impulsen
har en konstant verdi analogt med bevarelse av energi i et mekanisk problem. Nå er
hvor dx/ds er sinus til vinkelen θ som tangenten til lysbanen har, målt fra y-aksen. Derfor tilsvarer bevarelsen av denne størrelsen at Snells brytningslov gjelder lokalt i hvert punkt langs banen,
Variasjonsproblemet er nå redusert til å løse en første ordens differensialligning som vanligvis er enklere.
Man kan alternativt komme mer direkte frem til denne bevegelseskonstanten ved å parametrisere lysbanen ved den variable y i stedet for x som til nå. Da blir den optiske veilengden
hvor nå x' = dx/dy. I denne integranden opptrer ikke den variable x. Den er derfor syklisk, og den konjugerte impulsen
må være konstant, i.e. px = K. Dette gir igjen den lokale utgaven av Snells brytningslov da x'/√(1 + x' 2) = dx/ds som er sinus til den lokale brytningsvinkelen.
Eksempel[rediger | rediger kilde]
Noen optiske fenomen som fata morgana skyldes at brytningsindeksen avtar med høyden på grunn av temperaturinversjon. Antar man en plan jordoverflate, vil da n = n(y) og man kan beregne hvordan lyset går ved bruk av formalismen her. Som et enkelt eksempel kan man anta at brytningsindeksen varierer som
hvor n0 er verdien på jordoverflaten y = 0 og a er en konstant. Denne beskrivelsen kan da brukes så lenge som y < 1/a. Brytningsvinkelen til lyset oppfyller nå n(y) sinθ = n0 sinθ0 hvor verdiene på høyre side er de på jordoverflaten. Det betyr at banen til lyset er gitt ved dy/dx = cotθ. Dette kan uttrykkes ved sinθ og sammen med den valgte funksjonen n(y) finner man at
Direkte integrasjon gir nå løsningen
hvor x0 = sin2θ0 /a er en integrasjonskonstant som er bestemt ut fra betingelsen at lyset går ut fra x = 0 på jordoverflaten y = 0. Denne løsningen viser at det følger en parabel som når sitt høydepunkt y0 = cos2θ0 /a for x = x0 som definerer parabelens akse.[5]
Dette problemet kan også undersøkes ved bruk av formalismen i forrige seksjon. Det effektive potensialet blir nå
Bevegelsesligningen d v/dτ = - ∇V gir da at hastigheten vx i x-retning er konstant, mens hastigheten vy i y-retning er utsatt for en konstant akselerasjon g = - (1/2)an02. Dette tilsvarer problemet med kast av ball i tyngdefeltet. Ved tiden τ = 0 er vx = n0 sin θ0 og vy = n0 cos θ0 da v2 = n02 ved dette tidspunktet, det vil si for x = 0 der y = 0. Ved senere tidspunkt blir da x = n0 sin θ0τ og
Eliminerer man her den tidsvariable τ mellom disse to uttrykkene, finner man lett at
som er akkurat resultatet som ble tidligere funnet.
Referanser[rediger | rediger kilde]
- ^ O. Darrigol, A History of Optics, Oxford University Press, Oxford (2012). ISBN 978-0-19-876695-7.
- ^ E. Hecht, Optics, Addison-Wesley, Reading, Massachusetts (1998). ISBN 0-201-30425-2.
- ^ a b M. Born and E. Wolf, Principles of Optics, Pergamon Press, Oxford (1980). ISBN 0-08-026482-4.
- ^ J.L. Synge, Geometrical Optics, Cambridge University Press (1962). ISBN 978-0-521-06590-0.
- ^ E. Grønvoll og Ø. Grøn, Fra Fysikkens Verden, no. 3, p. 72 (2012)
Litteratur[rediger | rediger kilde]
- F. A. Jenkins and H. E. White, Fundamentals of Optics, McGraw-Hill Book Company, New York (1957).
Eksterne lenker[rediger | rediger kilde]
- R.P. Feynman, Principle of Least Time, Feynman Lectures on Physics





































