Ugyldige bevis
I matematikk er det et utvalg av uekte eller falske beviser av åpenbare motsigelser. Selv om bevisene er feilaktige er feilene, som regel konstruerte, utformet på en finurlig måte. Feiltagelse betraktes vanligvis som kuriositeter, men kan brukes til å vise viktigheten av de strenge prinsippene i matematikken.
Potenser og røtter[rediger | rediger kilde]
Bevis for at 1 = −1[rediger | rediger kilde]
Versjon 1[rediger | rediger kilde]
Start med likheten
Konverter begge sidene av ligningen til de vulgære brøkene
Ta kvadratroten av hver side for å få
Multipliser begge sidene med for å få
Enhver kvadratrot opphøyd i annen potens gir tallet selv slik at
Beviset er ugyldig fordi det misbruker følgende prinsipp for kvadratrøtter:
Dette gjelder kun hvis x og y er positive reelle tall hvilket ikke er tilfelle i beviset over.
Versjon 2[rediger | rediger kilde]
Ved å manipulere røtter ukorrekt, utleder man følgende falske bevis:
Q.E.D.
Regelen gjelder generelt bare hvis minst ett av tallene x og y er positivt, noe som åpenbart ikke er tilfelle her.
Versjon 3[rediger | rediger kilde]
Ved å gå inn og ut av domenet til de komplekse tallene, kan følgende falske bevis utledes:
Q.E.D.
Ligningen , hvor b og/eller c er brøker gjelder kun når a er positiv, hvilket ikke er tilfelle her, og dette leder derfor til det falske beviset.
Versjon 4[rediger | rediger kilde]
Start med Pythagoras likhet
Opphøy begge sider av ligningen til potensen 3/2 for å få
La
Q.E.D.
Dette beviset feiler på grunn av skritt nummer 3 hvor regelen anvendes uten forsikringen om at a er positiv. Også i fjerde skritt sjekkes ikke alle røttene av . Selv om 1 er et svar, er det ikke det eneste siden -1 også funker.
Bevis for at x=y for alle x, y[rediger | rediger kilde]
Hvis så er . Ettersom kan vi slutte at .
Q.E.D.
Feilen i dette beviset ligger i det faktum at den anvendte regelen kun gjelder for positive .
Bevis for at kvadratroten av -1 er 1[rediger | rediger kilde]
Q.E.D.
Feilen her ligger i den siste likheten hvor man ser bort fra de tre andre fjerderøttene til 1, som er -1, i og -i. Vi ser at vi har kvadrert tallet vårt, for så å ta røtter, og vi kan derfor ikke alltid anta at røttene vil være korrekte. De korrekte fjerderøttene er i og -i som er de imaginære tallene definert som . Ideen vises også i det neste beviset:
Bevis for at -2 = 2[rediger | rediger kilde]
Q.E.D.
Igjen er feilen at vi har introdusert et annet kvadrat ved å kvadrere for så å ta kvadratroten.
Å dele med null[rediger | rediger kilde]
Bevis for at 2 = 1[rediger | rediger kilde]
La a og b være forskjellige fra null
Multipliser med a
Trekk fra
Faktotiser begge sidene
Divider med
Legg merke til og sett inn at
Kombiner like ledd på venstresiden
Divider med b
Q.E.D.[1]
Feilslutningen ligger i linje 5: overgangen fra linje 4 til 5 involverer at man deler på , hvilket er null siden a er ekvivalent med b. Ettersom å dele med null er udefinert er argumentet ugyldig. Ved å utlede at den eneste mulige løsningen av linjene 5, 6 og 7 er , er feilen igjen åpenbar i linje 7 hvor man dividerer med b (0) for å komme frem til feilslutningen. Et lignende ugyldig bevis ville være å si at (hvilket er sant) og med å dele på null kommer man frem til at .
Bevis for at alle tall er lik 1[rediger | rediger kilde]
Anta at vi har følgende system av lineære ligninger:
Ved å dividere den første ligningen med , får vi La oss nå prøve å løse systemet med Cramers regel:
Da hver kolonne i koeffisientmatrisen er lik den resulterende kolonnevektoren har vi
for alle . Setter vi dette tilbake inn i , får vi
- .
Q.E.D.
Beviset er ugyldig fordi Cramers regel bare kan anvendes på systemer som har en unik løsning. I dette tilfellet derimot er alle ligningene åpenbart ekvivalente og utilstrekkelig for å gi en unik løsning. Feiltakelsen skjer når vi dividerer med , ettersom begge er null.
Bevis for at alle tall er like[rediger | rediger kilde]
Å multiplisere et vilkårlig tall med 0 gir svaret null.
Omskriving av ligningen gir
På samme måte har vi
og fordi
innsetting gir nå
Samme metode kan brukes til å vise at ethvert tall er likt ethvert annet tall og dermed er alle tall like.
Q.E.D.
Feilslutningen ligger i antagelsen om at divisjon med null gir en veldefinert verdi.
Calculus (differensialregning)[rediger | rediger kilde]
2 = 1 nok en gang[rediger | rediger kilde]
Ut fra den vanlige meningen av multiplikasjon har vi
Man ser også at for enhver x forskjellig fra null gjelder
multipliser denne ligningen med x
Ta deretter den deriverte med hensyn på x
Nå ser vi at høyre side er x som leder til
Siden x er forskjellig fra null kan vi dividere den ut og få
Q.E.D.
Problemet her ligger i linje to. Definisjonen av x antok at x var et heltall; ligningen gir ikke mening ellers. Funksjoner er kun deriverbare i et kontinuerlig rom f.eks. de reelle tallene, men ikke heltall. For en bestemt x er ligningen sann, men å derivere begge sidene må du ha en ligning av funksjoner og ikke heltall som vi har her. Høyresidefunksjonen med x-leddene er ingen meningsfull funksjon av reelle tall og derfor ikke deriverbar.
I tillegg har vi følgende problem. Når vi deriverer i linje 4 tas den med hensyn på hvert ledd individuelt og ikke med hensyn på antallet ledd. Dette blir feil siden antallet ledd er derivasjonsvariabelen x. Kjerneregelen anvendes ikke på denne siden av ligningen og dette er feil.
Bevis for at 0 = 1[rediger | rediger kilde]
Start med beregningen av det ubestemte integralet
Med delvis integrasjon la
slik at
som gir
som ved å samle like ledd blir
Q.E.D.
Feilen her ligger i uriktig bruk av delvis integrasjon. Når man anvender formelen må det legges til en tilfeldig konstant K på høyre side av ligningen. Dette kommer av utledningen av formelen for delvis integrasjon, som inneholder integreringen av en ligning. Vanligvis ser man bort fra denne konstanten helt til siste slutt, men her må konstanten legges til med en gang fordi de resterende integralene opphever hverandre.
Med andre ord er nest siste linje korrekt, men den siste linjen er ikke det. Du kan ikke fjerne fordi de nødvendigvis ikke er like. Det er uendelig mange antideriverte av en funksjon som alle skiller seg fra hverandre med en konstant. I dette tilfellet skiller konstantene seg med 1.
Problemet kan unngås hvis vi bruker bestemte integraler. I andre linje vil da 1 evaluert mellom noen grenser som alltid vil bli lik 1 - 1 = 0. De gjenstående integralene vil da være identiske.
Bevis for at 1 = 0[rediger | rediger kilde]
Start med påstanden
Ta den deriverte på hver side,
Den deriverte av x er 1 og den deriverte av 1 = 0, dermed.
Q.E.D.
Feilen i dette beviset er at x behandles som en variabel og ikke som en konstant som konstatert med x = 1, idet man deriverer den. Tar man den korrekte deriverte av konstanten x får man det riktige svaret 0 = 0.
Uendelige rekker[rediger | rediger kilde]
0 = 1 om igjen[rediger | rediger kilde]
Start med summasjonen av uendelig mange etterfølgende nuller
Legg merke til at
Ved å anvende den assosiative loven for addisjon får man
Det er opplagt at
tillegget med den uendelige summen av nuller kan fjernes slik at
Q.E.D.
Feilen her er at den assosiative loven ikke fritt kan anvendes på en uendelig sum med mindre summen konvergerer uten parenteser. Summen i dette tilfellet 1 − 1 + 1 − 1 + · · · er en klassisk divergent rekke. I argumentet her gir linje 2 rekken av delsummer 0, 0, 0, ... som konvergerer mot 0, mens linje 3 gir rekken av delsummer 1, 1, 1, ... som konvergerer mot 1, så uttrykkene trenger ikke være like.
Faktum er at den assosiative loven for addisjon kun sier noe om summer med tre ledd: . Det er enkelt å vise at loven gjelder for et begrenset antall summeringer (ved hjelp av induksjon). Men problemet ligger i uendeligheten. Det vil ta et uendelig antall skritt å komme dit og et matematisk bevis skal kun ta et endelig antall skritt for å komme i mål. En annen illustrasjon på dette er følgende "bevis" av som bare bruker konvergente uendelige summer og loven som gjør det mulig å bytte om to etterfølgende elementer i en slik sum, som definitivt er gyldig:
Bevis for at en rekke av positive ledd summerer til −1[rediger | rediger kilde]
Start med den uendelig geometriske rekken
Den velkjente formelen for summen av en uendelig geometrisk rekke er
hvor a0 er første ledd i rekken og r er felles forhold mellom leddene. Anvendelse av formelen gir
Q.E.D.
Feilen i beviset ligger i det faktum at en geometrisk rekke er konvergent hvis og bare hvis .
Bevis for at summen av alle positive tall er negativ[rediger | rediger kilde]
Definer konstantene S og A ved
- .
Derfor
Legger man sammen disse ligningene får man
Summen av alle positive tall er altså negativ.
Problemet med dette beviset er antakelsen divergente rekker følger aritmetikkens lover.
Uvedkommende løsninger[rediger | rediger kilde]
Bevis for at −2 = 1[rediger | rediger kilde]
Start med å prøve å løse denne ligningen
Opphøy begge sidene i tredje potens
Ved å bytte ut uttrykket i parentesene med den opprinnelige ligningen og fjerne/samle like ledd får man
Opphøy i tredje potens nok en gang gir
Hvilket gir løsningen x = 2. Setter man disse verdiene inn i den opprinnelige ligningen får man
og dermed
Q.E.D.
Når man går fremover viser argumentet ikke noe annet enn at det ikke finnes noen x som tilfredsstiller ligningen. Når du går baklengs fra x=2 ser man bort fra faktorene som også er kubiske røtter av 1. Når man opphøyer en ligning slik det her gjøres er ikke ligningen den samme lenger og den produserer ofte ekstra løsninger. Det kan nevnes at ethvert tall har 3 kubiske røtter, 1 reell og 2 komplekse. (Hvis tallet i seg selv er komplekst har det 3 komplekse røtter.)
Bevis for at 3 = 0[rediger | rediger kilde]
Anta følgende ligning for en kompleks x :
Da:
Divider med x (anta x forskjellig fra 0)
sett inn det siste uttrykket for x i den originale ligningen og få:
sett inn x=1 i den originale ligningen igjen:
Q.E.D.
Feilslutningen her er antagelsen om at som impliserer . Faktum er at det er 3 kubikkrøtter av 1, hvorav de to komplekse er løsninger av den opprinnelige ligningen. Innsettingen introduserer den tredje som er reell som en uvedkommende løsning. Ligningen etter innsettingen skrittet følger av den foregående, men implikasjonen gjelder ikke motsatt vei, hvilket betyr at overgangen introduserer nye løsninger.
Komplekse tall[rediger | rediger kilde]
Bevis for at 1 = 3[rediger | rediger kilde]
Fra Eulers formel ser man at
og
slik at
tar man den naturlige logaritmen på begge sider får man
Dividerer man med πi får man
QED.
Feiltakelsen er at regelen generelt bare er gyldig for reelle verdier av x, og altså ikke komplekse x. Den komplekse logaritmefunksjonen er multivariabel; og for alle heltall k. Vi ser dermed at og er to av den uendelige mengden tall som svarer til ln(-1) i det komplekse plan.
Beviset x = y for alle reelle x, y[rediger | rediger kilde]
La x og y være to tall. Deretter sett La også Beregn så:
Ved å sette inn får vi:
Regn så ut Innsetting av :
slik at:
Innsetting :
Q.E.D.
Feilslutningen er at fra z³ = w³ kan man ikke generelt avlede z = w (med mindre z og w begge er reelle, hvilket ikke er tilfelle her).
Ulikheter[rediger | rediger kilde]
Bevis for at 1 < 0[rediger | rediger kilde]
La oss først anta at
Nå tar vi den naturlige logaritmen på begge sidene. Så lenge x > 0, kan vi gjøre dette ettersom logaritmefunksjonen er monotont økende. Nå legger vi merke til at logaritmen til 1 er 0 så vi får
Dividerer vi med ln (x) gir dette
Q.E.D.
Det kritiske her er divisjonen i det siste skrittet. Dette er ugyldig siden ln(x) er negativ for 0 < x < 1. Mens multiplikasjon eller divisjon av positive tall bevarer ulikheten, medfører den samme operasjonen med negative tall en reversering. Altså skal man snu ulikheten og få det korrekte resultatet 1 > 0.
Uendelig[rediger | rediger kilde]
Bevis for at ∞ = 1/4[rediger | rediger kilde]
Ettersom et uendelig stort plan har koordinater (-∞,∞) × (-∞,∞), betyr dette at
noe som kan forenkles til
og til slutt
Kombiner nå de ulike ∞:
Som igjen kan forenkles til
og til sist for å finne verdien av ∞,
Dette kan verifiseres med å starte med den opprinnelige ligningen,
Sett inn verdien man har funnet for ∞:
som forenkles til
som til slutt blir
Q.E.D.
Feilen i beviset ligger i anvendelsen av ∞ (uendelig) til å representere en endelig verdi – men uendelig er i realiteten å tenke på som en retning i motsetning til målet. En av de mer uvanlige aspektene av denne typen ugyldige beviser er at det kan verifiseres, spesielt i motsetning til de hvor man deler med null. Uendelig dividert med seg selv er også udefinert.
Eksempler fra geometrien[rediger | rediger kilde]
Bevis for at enhver vinkel er null[rediger | rediger kilde]
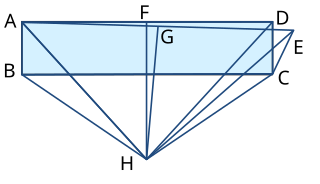
Konstruer et rektangel ABCD. Identifiser et punkt E slik at CD = CE og vinkelen DCE er en vinkel forskjellig fra null. Ta den normale halveringslinjen av AD, som krysser F, og den normale halveringslinjen av AE, som krysser i punktet G. Kall punktet hvor normalene krysser hverandre H og forbind dette punktet med A, B, C, D og E
Nå er AH = DH ettersom FH er en vinkelrett halveringsvinkel; likeså er BH = CH. AH = EH ettersom GH er en vinkelrett halveringsvinkel og DH = EH. Rektanglet i utgangspunktet gir også BA = CD = CE slik at trekantene ABH, DCH og ECH er kongruente, og vinklene ABH, DCH og ECH er like.
Men hvis vinklene DCH og ECH er like, må vinkelen DCE være null.
Q.E.D.
Feilen i beviset kommer frem i diagrammet og i det siste punktet. Et nøyaktig diagram hadde vist at trekanten ECH er en refleksjon av trekanten DCH om linjen CH og ikke på samme side. Så selv om vinklene DCH og ECH er like i størrelse, er det ingen ting som rettferdiggjør en subtraksjon mellom disse. For å finne vinkelen DCE må man trekke vinklene DCH og ECH fra vinkelen til en hel sirkel (2π or 360°).
Bevis for at ethvert parallellogram har uendelig areal[rediger | rediger kilde]
Ta et parallellogram ABCD. Trekk uendelig mange streker like lange og parallelle med CD langs AD's lengde helt til parallellogrammet er fullt av slike linjer. Ettersom linjene er like lange som CD er det totale arealet av disse og dermed parallellogrammet ∞ × (CD), altså uendelig.
Q.E.D.
Problemet med dette beviset er at en linje ikke representerer et areal, og kan ikke anvendes på denne måten. I tillegg er ikke uendelig et reelt tall og anvendes ikke i tradisjonelle geometriske beregninger.
Referanser[rediger | rediger kilde]
- ^ Harro Heuser: Lehrbuch der Analysis – Teil 1, 6. utgave, Teubner 1989, ISBN 978-3835101319, side 51 (Tysk).































































































![{\displaystyle {\sqrt[{3}]{1-x}}+{\sqrt[{3}]{x-3}}=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea0d9c7ce6521842fa9138d487f72a395c302721)
![{\displaystyle (1-x)+3{\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}\ ({\sqrt[{3}]{1-x}}+{\sqrt[{3}]{x-3}})+(x-3)=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60652f1d46a792f6eb35b505b1a425501e1b5d1)
![{\displaystyle -2+3{\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62a48c8f23a2ce04df0d66bb7a962957c34139fb)
![{\displaystyle {\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d1b5bec4368bf804b2037b93b0cbca76013998)



![{\displaystyle {\sqrt[{3}]{1-2}}+{\sqrt[{3}]{2-3}}=1\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05cdce078f16b89696d32ae7dd7e1f771432bc86)
















































![{\displaystyle {\frac {}{}}\infty =[\infty -(-\infty )]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9148a203f9e41ab4289c1743bfeb4a021eb730a4)





![{\displaystyle {\frac {1}{4}}=\left[{\frac {1}{4}}-\left(-{\frac {1}{4}}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d54dbb987b770a65d6067da9f5ec9341ecb184f9)
![{\displaystyle {\frac {1}{4}}=\left[{\frac {1}{2}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93f9c0ac7598048f1aca60edcb62127b157fde61)
