Euklids algoritme
Euklids algoritme er en fremgangsmåte for å beregne på en systematisk måte den største felles divisor til to elementer som tilhører en euklidsk ring. I det enkleste tilfelle benyttes den for heltall. Algoritmen er en av de eldste som er kjent og har fått sitt navn etter den greske matematiker Euklid. Han beskrev den i sitt hovedverk Elementer som kan dateres tilbake til antikkens Hellas. Den samme fremgangsmåten kan også benyttes til å forenkle generelle brøker og har mange anvendelser i moderne tallteori.
Bakgrunn[rediger | rediger kilde]
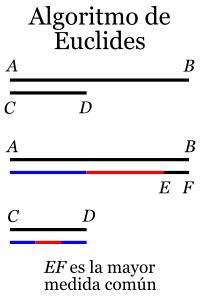
Fremgangsmåten som beskrives i algoritmen var sannsynligvis godt kjent på Euklids tid tog ble omtalt som antanairesis. Sannsynligvis stammer metoden helt tilbake til babylonerne. Den fremkommer på en naturlig måte når man skal måle nøyaktig en avstand med en målestav med kjent lengde, men uten noen finere inndeling. Men man kan merke av kortere lengder på denne.[1]
Hvis den søkte avstanden kalles a og målestaven har lengde b, kan man si at denne utgjør den lengdeenhet man vil benytte. Man ønsker derfor å måle a i enheter av b, det vil si forholdet a/b. Dette tilsvarer da en divisjon, og man vil generelt ikke finne noe noe heltallig svar.
Fremgangsmåte[rediger | rediger kilde]
Først måler man hvor mange hele ganger q0 som b kan plasseres langs a. Generelt vil det da oppstå en rest r0 < b. Når denne er forskjellig fra null, sier man at målingen eller divisjonen ikke «går opp» og man har
I neste omgang bestemmer man hvor mange ganger q1 avstanden r0 er inneholdt i b. Det vil eventuelt gi en ny rest r1, og man har
hvor nå r1 < r0. På denne måten fortsetter man og måler hvor mange ganger r1 er inneholdt i r0,
Generelt vil man etter å ha gjentatt dette n ganger at
Denne fremgangsmåten kan fortsette helt til restene er blitt forsvinnende små, og man er fornøydd med resultatet. Det kan da generelt skrives som en kjedebrøk. Stopper man for eksempel etter n = 2 ganger der man kan sette r3 = 0, vil man ha at r2 = r1/q3. Innsatt i den forrige ligningen, har man da r1 = r0 /(q2 + 1/q3). Herav kan så r0 bestemmes uttrykt ved lengden b. Resultatet er da kjedebrøken a/b = [q0;q1,q2,q3] som utskrevet er
I prinsippet gir denne fremgangsmåten et resultat som kan bli så nøyaktig som man ønsker ved å foreta disse gjentagelsene lenge nok.[2]
Største felles faktor[rediger | rediger kilde]
Den samme algoritmen kan også bli benyttet til å finne største felles faktor av to tall a og b. Hvis man etter n stepp finner at resten rn+1 = 0, vil denne felles faktor være den foregående resten rn. De to tallene sies da å være kommensurable.[2]
Som et konkret eksempel kan man betrakte tallene a = 551551 og b = 50065. Da får man videre fra algoritmen
Største felles faktor for 551551 og 50065 er derfor 19.
Dataprogram[rediger | rediger kilde]
Algoritmen til Euklid er rekursiv og kan derfor lett implementeres på en elektronisk datamaskin. Man kan da definere en funksjon SFD(a,b) som gir største felles divisor av de to heltallene a og b. Strukturen til programmet vil da være
funksjon SFD(a, b)
hvis b = 0 returner a
ellers returner SFD(b, a mod b)
Her benyttes den innebygde modulo-funksjonen mod som gir resten etter en heltallsdivisjon.
I programmeringsspråkene C++ eller Java vil algoritmen se ut som
int SFD(int a,int b){
if ( b == 0 )
return a;
return SFD(b,a%b);
}
hvor modulo-funksjonen betegnes med prosentsymbolet %.
Faktorisering av polynom[rediger | rediger kilde]
Polynom kan adderes og multipliseres sammen. De kan på den måten danne en matematisk ring med tilsvarende egenskaper som heltallene Z. Av den grunn kan et polynom ofte faktoriseres i et produkt av et eller flere andre polynom av lavere grad. Denne faktorisering kan også systematisk utføres ved hjelp av Euklids algoritme.[3]
Hvis man er gitt ett polynom a(x) og et annet b(x) av samme eller lavere grad, kan man alltid foreta en oppsplitting av formen
hvor de to polynomene q(x) og r(x) entydig kan bestemmes. Polynomet b(x) kan så splittes opp på en tilsvarende måte og dermed gi opphav til et nytt restpolynom r(x) . Denne prosessen fortsettes så til man står igjen med et restpolynom som er null. Den største felles faktor av polynomene a(x) og b(x) er da det foregående restpolynomet.
Fremgangsmåten kan illustreres ved et enkelt eksempel der
Da er
- ,
slik at den felles faktor er . Polynomet a(x) kan derfor splittes opp og man finner
Det er først når de gitte polynomene har mye høyere grad, at denne algoritmen virkelig kommer til sin fulle bruk.
Se også[rediger | rediger kilde]
Referanser[rediger | rediger kilde]
- ^ A. Holme, Matematikkens historie, Bind 1, Fagbokforlaget, Bergen (2002). ISBN 82-7674-678-0.
- ^ a b O. Ore, Number Theory and Its History, Dover Publications, New York (1988). ISBN 0-486-65620-9.
- ^ J. Reed og J. Aarnes, Matematikk i vår tid, Universitetsforlaget, Oslo (1967).
Eksterne lenker[rediger | rediger kilde]
- J. O'Connor and E. Robertson, Division and Euclidean algorithms Arkivert 6. mai 2021 hos Wayback Machine., University of St. Andrews, Scotland












