Tellebord

Et tellebord er et hjelpemiddel tidligere brukt til å utføre enkle beregninger: addisjon, subtraksjon, multiplikasjon og divisjon.[1] Det er den eldste kjente form for redskap til å telle med og til aritmetiske operasjoner, når en ser bort fra hender og fingre og andre primitive hjelpemidler.[2] Tellebordet var en forløper for abakusen og mye brukt i middelalderen til praktiske beregninger.
Utforming[rediger | rediger kilde]

Tellebordet var en plate laget av stein eller tre, og løse perler, steiner, trestykker eller farget sand ble lagt og flyttet på brettet for å utføre beregninger. På bordet ble et sett av parallelle linjer brukt til å markere tiere, som 1, 10, 100 og 1000. Vanligvis ble linjene plassert horisontalt i forhold til brukeren, med linjen for 1 nærmest brukeren.
For å indikere et gitt tall ble steinene plassert på og mellom linjene. En stein plassert mellom to linjer ble brukt for å markere 5, 50, 500, ... Tallet 218 kunne representeres ved å legge tre steiner på ener-linjen, én stein mellom ener- og tier-linjen, én stein på tier-linjen og to steiner på hundre-linjen.
Ordet «kalkulere» betyr opprinnelig «å bruke småstein».[3] Det latinske ordet calculus betyr «småstein». Roten i dette ordet, «calx», er den samme som i kalk.
Regneoperasjoner[rediger | rediger kilde]
Addisjon[rediger | rediger kilde]
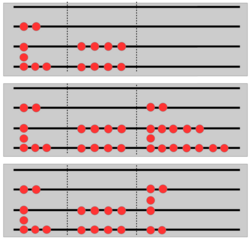
For å legge sammen to tall var det kun nødvendig å vite hvordan et tall var representert på brettet, kunne telle til fem samt legge sammen tall under fem.[1] De to tallene som skulle summeres ble lagt ut adskilt, men ved siden av hverandre på brettet. På hver linje og for hvert linje-mellomrom summerte en antallet steiner, og resultatet ble brukt til å legge ut et nytt tall - summen. Fikk en flere enn fem steiner på en linje, ble fire fjernet og én stein flyttet opp på mellomrommet over. Fikk en to steiner i et mellomrom, ble én stein fjernet og én flyttet opp på linjen over.
Eksempelet til høyre viser tre stadier i summasjonen 218 + 44 = 262. I første trinn legges ut de to addendene, og deretter summeres linje for linje og mellomrom for mellomrom. I tredje trinn reorganiseres steinene på de ulike nivåene.
Subtraksjon[rediger | rediger kilde]

For å subtrahere to tall ble igjen begge tallene lagt ved siden av hverandre på brettet. For hver linje og mellomrom legger en ut svaret, ved å trekke antall steiner i den andre tallet fra antallet i det første. En kan da komme i en situasjon at en må «låne» en stein fra linjen eller mellomrommet over, og da gjøre om denne til henholdsvis fem eller to steiner.
Eksempelet til høyre viser stadier i utføring av beregningen 218 - 44 = 174. I første trinn legges ut subtrahenden 218 og minuenden 44. I trinn to er siffer i subtrahenden gjort om, ved å låne fra nivået over, og deretter er differensen beregnet.
Multiplikasjon[rediger | rediger kilde]

For å multiplisere et tall med 10 er det tilstrekkelig å kopiere representasjonen av på ett linjenivå høyere. Tilsvarende kan en multiplisere med 100 ved å kopiere det opprinnelige tallet to linjenivå opp.
For å multiplisere to vilkårlige tall, som 113 22, så kunne dette utføres ved først å legge ut representasjonen av 100 22, deretter 10 22 og til slutt tallet 22 tre ganger. Det endelige svaret ble funnet ved å addere steinene for alle mellom-resultatene. Dette er vist i eksempelet til høyre.
Divisjon[rediger | rediger kilde]
Divisjon var komplisert å utføre med tellebordet, og flere forskjellige metoder var i bruk.[1] Brukeren måtte være i stand til å gjette antall tier-potenser i svaret og så bruke subtraksjon til å bryte ned beregningen.
Historie[rediger | rediger kilde]

Ikke mange tellebord er bevart, på grunn av det forgjengelige materialet som ofte ble benyttet for å lage dem.
Det eldste kjente tellebordet er Salamistavlen, funnet på den greske øya Salamis i 1899.[2] Brettet er datert til ca. 300 f.Kr., og det er antatt at brettet opprinnelig har vært benyttet av babylonere som spillebord eller som redskap for kalkulering. Tavlen er laget av marmor, og størrelsen er 150 x 75 x 4.5 cm. Det har innskåret greske bokstaver, sammen med parallelle streker skåret som fordypninger. Salamistavlen er i dag oppbevart i Det greske nasjonalmuseum i Athen.[2]
Tellebordene ble tildels fortrengt av bruken av kulerammer (abakus), men er lite er kjent om når og hvordan dette skjedde.[4]
De første trykte aritmetikkbøkene som kom ut på henholdsvis italiensk (1478) og tysk (1482) var begge forfattet av en «Rechenmeister» fra Nûrnberg.[5] Begge bøkene baserer seg på bruk av tellebord, beskrevet som «beregning på linjer». Bøkene var beregnet for lærere i aritmetikk. Den tyske matematikeren Adam Ries ga ut sin første bok Rechnung auff der linihen i 1518, og også denne brukte «linjekalkulasjon». Den neste boken hans, Rechnung auff der Linien und Federn, startet med «linjekalkulasjon», men gikk raskt over til bruk av «de nye tallene».
Den første kjente engelske trykte boken om aritmetikk kom i 1539, og boken refererer til beregninger «med penn eller med tellebord».[1] Også Robert Recordes bok Ground of Artes fra 1542 hadde et avsnitt om tellebord.
Se også[rediger | rediger kilde]
Referanser[rediger | rediger kilde]
- ^ a b c d : F.J Swetz; The European Mathematical Awakening s.5ff
- ^ a b c «Ancient Counting Boards» Arkivert 3. januar 2008 hos Wayback Machine.
- ^ Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9. s.39
- ^ C.B.Boyer (1968). A history of mathematics. Princeton, USA: John Wiley & Sons, Inc. ISBN 0-691-02391-3. s.220
- ^ : F.J Swetz; The European Mathematical Awakening s.45ff
Litteratur[rediger | rediger kilde]
- Vera Sanford (2013). «Counters: Computing if you can count to five». I Frank J. Swetz. The European Mathematical Awakening. Mineola, New York: Dover Publications. ISBN 0-486-49805-0.


