Abakus (kuleramme)
- Abakus har også andre betydninger
Abakus (latin abacus; gresk abax eller abakos) eller kuleramme er et gammelt regnehjelpemiddel som består av en plate eller en ramme med staver eller tråder der kuler kan skyves frem og tilbake. Antagelig er det greske ordet avledet fra et enda eldre hebraisk ord abhaq, som betyr sand eller støv).

Man kan si at abakus er i slekt med andre løsninger som benytter repeterende ting for tallrelaterte gjøremål: quipu for å huske tall og andre info med knuter på hyssingbunt, yupana med sine symbolske åker hvor man kunne plassere et antall frø i hver, rosenkrans eller bønnekjede for å telle antall ganger en har gjentatt et gjøremål, og knopetau, en line med knoper (knuter) til å måle fart under seiling.
Bruksmåte[rediger | rediger kilde]
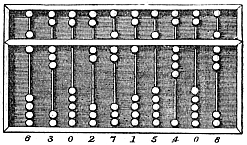
De vertikale stavene eller trådene representerer, regnet fra høyre til venstre, entall, titall, hundretall osv.
Kulene i den nedre gruppen har hver og en verdien 1 (når ført oppover mot skillelisten mellom gruppene), eller verdien 0 (når kulen er skjøvet nedover).
Kulene i den øvre gruppen har hver og en verdien 5 (når ført nedover mot skillelisten mellom gruppene), eller verdien 0 (når skjøvet oppover).
De syv kulene på en stav kan stilles inn i 16 forskjellige kombinasjoner, hvormed først og fremst alle siffer fra 0 til 9 kan representeres (dekadisk regning). De overskytende kombinasjonene kan representere sifrene A til F ved hexadesimal regning.
Summen av kulenes innstilte verdi langs en av stavene representerer det betraktede tallets verdi.
Ved å skyve kulene frem og tilbake i henhold til visse regler kan man håndterer de fire enkle regneoperasjoner addisjon, subtraksjon, multiplikasjon og divisjon. Men muligheten er ikke uttømt med det: det finnes regler for uttrekning av både kvadratrøtter og kubikkrøtter. Fjerde rot kan beregnes ved at man bestemmer kvadratroten to ganger suksessivt.
En vant abakusregner finner rett resultatet raskere enn det som var mulig med elektromekaniske addisjonmaskiner og s k regnesnurrer av type Original-Odhner.
I Norge har blinde (som ikke så lett kan regne med papir og blyant) fått undervisning i bruk av abakus. Det ble utviklet en egen Huseby abakus med plastperler som beveger seg i plastlister. Abakusen er laget slik at perlene ikke flytter seg så lett når selv om du kommer borti dem. (Listene og perlene er opprinnelig laget til gardinoppheng.)
Hvis du bruker hendene som abakus kan du telle til 99 på fingrene: Du har fire enere og en femmer på den ene hånden; fire tiere og en femtier på den andre.
Historie[rediger | rediger kilde]
Før abakus improviserte man med avlange parallelle groper hvor man plasserte småsteiner/frø og flyttet disse langs egen grop for å utføre beregninger. I Europa var det vanlig med regnebord påtegnet linjer som man plasserte og flyttet lekepenger oppå.
Abakus er nok en fortsettelse av tidligere tiders fingertelling eller daktylonomi som gir mulighet til de samme aritmetiske operasjoner og er kjent fra gammelt av.[1] Fordelen med abakus er :
- hendene blir frigjort for andre formål,
- operasjonene krever mindre ubekvem fingerbøyning og derfor tid,
- mellomberegningen huskes ved avbrudd,
- den er praktisk for tall mye større enn det som fingertelling kan benyttes til, og
- det er et enklere kognitiv prosess å representere og lese større tall på en abakus.
Den er kjent særlig fra Antikken og fra mange utomeuropeiske kulturer. Kulerammer av diverse modeller brukes fortsatt iblant i for eksempel Japan og Kina. Den japanske versjonen kalles soroban, den kinesiske suan pan. Ved bruk legges rammen på et bord eller holdes på kneet med stavene rettet langsetter betraktningsretningen.
Abakus mistet sin dominerende posisjon hos handelsstanden etter at indo-arabiske sifre og aritmetiske operasjoner gradvis ble tatt i bruk i perioden 11. til 14. århundre. Abakus beregninger som ikke kunne dokumenteres (typisk ble kun resultatet notert i rømertall) tapte mot sifferoperasjoner på papir som egnet seg for kontroll i ettertid. Dette tok spesielt fart etter at Fibonacci publiserte metodikken bl.a. i hans store verk Liber Abaci "Regnekunsten" og en mindre men mer populær manual for handelsfolk.
Referanser[rediger | rediger kilde]
- ^ «Dactylonomy». Laputan Logic. 16. november 2006. Arkivert fra originalen . Besøkt 12. mai 2012. «Arkivert kopi». Arkivert fra originalen 23. mars 2012. Besøkt 3. januar 2016.
Litteratur[rediger | rediger kilde]
- Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9.
