Sadelpunkt

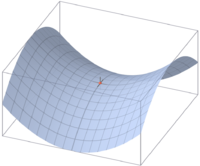
Grafen til funksjonen z=x²−y², punktet (0,0) (her rødt) er et eksempel på et sadelpunkt. Det er et minimumspunkt om vi beveger oss gjennom det langs x-aksen og et maksimumspunkt langs y-aksen.

Et sadelpunkt er, innenfor matematikken, et punkt på en graf som er stasjonært, men ikke et ekstremalpunkt. I et sadelpunkt er alltid den deriverte lik null, som i ekstremalpunkter. Navnet kommer av den hestesadellignende formen som på bildet.

Maksimum, minimum og sadelpunkter kan undersøkes ved funksjonens andrederiverte i det aktuelle punktet. For en funksjon f(x,y), kan man derivere to ganger med hensyn på x for å finne x-ens dobbeltderiverte (fxx) og likeså med hensyn på y (fyy), kan vi derivere med hensyn på x en gang og med hensyn på y en gang for å få den dobbeltderiverte fxy. Om fxxfyy-fxy^2 er negativ er punktet et sadelpunkt (om det er positivt er det enten et maks.- eller minimumspunkt, dersom fxx og fyy er negative er det et maksimalpunkt, om begge er positive er det et minimumspunkt).