k-means
Språkvask: Teksten i denne artikkelen kan ha behov for språkvask for å oppnå en høyere standard. Om du leser gjennom og korrigerer der nødvendig, kan du gjerne deretter fjerne denne malen. |
k-means er en grupperingsalgoritme som brukes i informatikk, kunstig Intelligens og matematisk optimering for å klassifisere enheter i kategorier eller grupper, såkalt klynging. Den brukes mye i datautvinning. k-means lar en velge antall kategorier (k). Algoritmen kategoriserer enhetene automatisk og gjør seg ferdig når den har kommet frem til faste kategorier.
Beskrivelse
[rediger | rediger kilde]k-means er en vektorkvantiseringsmetode som opprinnelig kommer fra signalbehandling. Den er populær innen grupperingsanalyse i datautvinning. k-means forsøker å inndele n observasjoner i k grupper, hvor hver observasjon hører til gruppens nærmeste gjennomsnitt, som fungerer som en prototype for gruppen. Dette resulterer i en inndeling av dataområdet i Voronoi-celler.
Problemet er beregningsmessig vanskelig, men det finnes effektive heuristiske algoritmer som vanligvis blir anvendt og som raskt samles til et lokalt optimal. Disse ligner vanligvis på forventnings-maksimeringsalgoritmen for blandinger av normalfordelinger via en iterativ justeringstilnærming brukt av begge algoritmer. I tillegg bruker begge gruppe-sentere for å modellere informasjonen; derimot har k-means en tendens til å finne grupper av sammenlignbar utbredelse, mens forventnings-maksimeringsmekanismen tillater grupper med forskjellige former.
Bakgrunn
[rediger | rediger kilde]Termen «k-means» ble først brukt av James MacQueen i 1967 [1], selv om ideen først ble beskrevet av Hugo Steinhaus i 1957[2]. Standardalgoritmen ble først foreslått av Stuart Lloyd i 1957 som en teknikk for PCM, selv om den ikke ble publisert utenfor Bell Labs før 1982[3]. I 1965 publiserte E. W. Forgy en metode som essensielt er den samme. På grunn av dette er metoden av og til referert til som Lloyd-Forgy [4]. En mer effektiv versjon ble foreslått og publisert i Fortran av Hartigan og Wong i 1975/1979[5][6].
Algoritmen
[rediger | rediger kilde]Gitt et sett av observasjoner (x1, x2, …, xn), hvor hver observasjon er en d-dimensjonal reell vektor, forsøker k-means å dele inn de n observasjonene i k (≤ n) sett S = {S1, S2, …, Sk} for å minimere summen av “within-cluster sum of squares” (WCSS), altså summen av kvadrater innenfor gruppen. Med andre ord forsøker den å finne:
hvor µi er gjennomsnittet av punktene i Si.
Standardalgoritmen
[rediger | rediger kilde]Den mest vanlige algoritmen bruker en iterativ justeringsteknikk. På grunn av sin utbredelse er den ofte bare referert til som k-means algoritmen. Den er også referert til som Lloyd’s algoritme, spesielt innenfor informatikk-miljøet.
Initiering
- Putter alle verdiene inn
- Velger k tilfeldige verdier som senter.
Løkke
- Legger alle verdier inn i grupper basert på nærmeste senter
- Kalkulerer nytt senter basert på gjennomsnittet av alle verdiene i en klynge.
- Fortsetter til center ikke flytter seg.
Demonstrasjon av standardalgoritmen
-
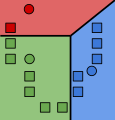
k “gjennomsnitt” ved start (i dette tilfellet k = 3) blir tilfeldig generert innenfor data-domenet (vist i fargene rød, grønn og blå).
-
k grupper lages ved å assosiere hver observasjon med det nærmeste gjennomsnittet. Partisjonene her representerer Voronoi-diagrammet generert av gjennomsnittene.
-
Sentroiden av hvert av de k gruppene blir det nye gjennomsnittet.
-
Steg 2 og 3 repeteres til konvergens har blitt nådd (sentroidene flytter seg ikke).
Algoritmen i seg selv tar inn alle elementene som skal sorteres. Deretter velger den tilfeldige verdier som senter for hver kategori. I dette eksempelet brukes tre kategorier, og algoritmen velger da ut tre tilfeldige sentre. Videre legges alle elementene inn i kategorien tilhørende senteret de har kortest euklidisk distanse til. I siste fase av løkken regnes nye sentere ut basert på gjennomsnittet av alle verdiene i kategoriene. Deretter legges verdiene på nytt inn i kategoriene som nå er nærmest, basert på eukledisk distanse.
Dette fortsetter til alle kategorienes senter slutter å endre seg. Dette vil si at alle verdiene har funnet en kategori som passer og kategorienes sentroider har stabilisert seg.
Variasjoner
[rediger | rediger kilde]- Jenks natural breaks optimization
- k-medians-gruppering
- k-medoids
- Fuzzy C-Means Clustering
- Gaussian mixture (gaussisk miks)
- Flere metoder for å velge bedre startgrupper, for eksempel k-means++
- Filtreringsalgoritmen bruker kd-trær for å øke hastigheten på hvert k-means steg
- Noen metoder forsøker å øke hastigheten på hvert k-means steg ved å bruke coresets eller triangelaksiomet
- Unnslippe lokale optima ved å bytte punkter mellom klynger
- Den sfæriske k-means-algoritmen passer godt til retningsdata
- Minkowski metric weighted k-means forholder seg til irrelevante trekk ved å tilegne gruppe-spesifikke vekter til hvert trekk
Referanser
[rediger | rediger kilde]- ^ MacQueen, J. B. (1967). Some Methods for classification and Analysis of Multivariate Observations. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. 1. University of California Press. Besøkt 7. april 2009.
- ^ Steinhaus, H. (1957). «Sur la division des corps matériels en parties». Bull. Acad. Polon. Sci. 4 (12): 801–804. MR 0090073. Zbl 0079.16403.
- ^ Lloyd, S. P. (1957). «Least square quantization in PCM». Bell Telephone Laboratories Paper. Published in journal much later: Lloyd., S. P. (1982). «Least squares quantization in PCM» (PDF). IEEE Transactions on Information Theory. 28 (2): 129–137. doi:10.1109/TIT.1982.1056489. Besøkt 15. april 2009.
- ^ E.W. Forgy (1965). «Cluster analysis of multivariate data: efficiency versus interpretability of classifications». Biometrics. 21: 768–769.
- ^ J.A. Hartigan (1975). Clustering algorithms. John Wiley & Sons, Inc.
- ^ Hartigan, J. A.; Wong, M. A. (1979). «Algorithm AS 136: A K-Means Clustering Algorithm». Journal of the Royal Statistical Society, Series C. 28 (1): 100–108. JSTOR 2346830.