Andregradsflate

En andregradsflate er i matematikken definert som løsningsmengden til et kvadratisk polynom med flere ukjente. Den kan betraktes som en hyperflate i et affint rom med en dimensjon som er gitt ved antall ukjente i polynomet. Med to ukjente reduseres denne flaten til et kjeglesnitt i planet. Av den grunn kalles kalles også løsningsmengden med tre ukjente for en kjeglesnittsflate. I det generelle tilfellet med n ukjente gir polynomet opphav til en hyperflate i n dimensjoner og omtales vanligvis som en kvadrikk. Den er et eksempel på en matematisk varietet.
Hvis de n ukjente kalles x1, x2, ... , xn, kan de betraktes som koordinater i det omsluttende, affine rommet. Ligningen som definerer andregradsflaten har da den generelle formen
der aij er elementer i en n × n matrise som man kan anta er symmetrisk. Likedan utgjør bi komponentene til en n-dimensjonal vektor og c er en konstant. Disse parametrene tar vanligvis verdier som er reelle eller komplekse tall. Ligningen kan derfor skrives på den mer kompakte formen
hvor xT er en linjematrise som er den transponerte av kolonnematrisen x.
I matematiske undersøkelser av egenskapene til andregradsflater er det ofte av interesse å utvide det omsluttende rommet til å være et projektivt rom med koordinater X = (x0, x1, x2, ... , xn). Det affine rommet kan da avgrenses ved å sette x0 = 1. Kvadrikken tar da den enda mer kompakte formen
hvor nå A er en (n + 1)×(n + 1) symmetrisk matrise gitt som
I Den opprinnelige ligningen for den tilsvarende hyperflaten fremkommer da ved å benytte at xT b = bT x.
Tre dimensjoner[rediger | rediger kilde]
Når det omsluttende rommet har n = 3 dimensjoner, representerer løsningsmengden en todimensjonal flate. Ved en diagonalisering vil da den definerende ligningen kunne reduseres til forskjellige normalformer hvorav mange er av formen
når den har sitt senter i origo (0,0,0). I det tredimensjonale rommet finnes det 16 slike forskjellige normalformer. De mest interessante er følgende:
| Flate | Ligning | Form |
| Ellipsoide | 
| |
| Rotasjonsellipsoide eller sfæroide (spesialtilfelle av ellipsoide) | ||
| Kule (spesialtilfelle av rotasjonsellipsoide) | ||
| Elliptisk paraboloide | 
| |
| Sirkulær paraboloide (spesialtilfelle av elliptisk paraboloide) | ||
| Hyperbolsk paraboloide | 
| |
| Enkappet hyperboloide | 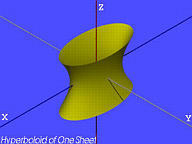
| |
| Tokappet hyperboloide | 
| |
| Kjegle | 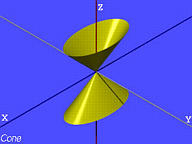
| |
| Elliptisk sylinder | 
| |
| Sirkulær sylinder (spesialtilfelle av elliptisk sylinder) | ||
| Hyperbolsk sylinder | 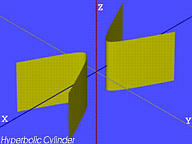
| |
| Parabolsk sylinder | 
|
Se også[rediger | rediger kilde]
Eksterne lenker[rediger | rediger kilde]
- Silvio Levy, Quadrics in Geometry Formulas and Facts Arkivert 18. juli 2018 hos Wayback Machine., CRC Standard Mathematical Tables and Formulas, CRC Press, 30. opplag.
- PlanetMath, Quadratic Surfaces.


















