Tabell (datastruktur)
En tabell (engelsk: array) i informatikk er en datastruktur bestående av en samling objekter som kan indekseres. I de fleste programmeringsspråk tilhører hvert element den samme datatypen og tabellen okkuperer et sammenhengende minneområde.
De fleste programmeringsspråk har en innebygget tabell-datatype, selv om denne i noen tilfeller egentlig er en assosiativ tabell. Tabell-datatypen kan også gå under andre navn som vektor og liste.
Tabeller kan enten ha en fast størrelse som ikke kan endres når de først har blitt allokert, eller de kan være dynamiske og endre størrelse etter behov.
De kan også være én-, to- eller flerdimensjonale. Det kreves da én indeks for hver dimensjon.
Egenskaper[rediger | rediger kilde]
Tabeller tillater vilkårlig tilgang til de enkelte elementene i konstant tid (O(1)). Dette er optimalt, men flytting av elementer tar tid som er proporsjonal med antall elementer som flyttes. Avhengig av maskinvaren, for eksempel dersom maskinen har en cache, vil sekvensiell iterering over tabellen være raskere enn å hente ut tilfeldige elementer. Dette skyldes at tabeller har god lokalitet ettersom de opptar et kontinuerlig stykke minne.
Tabeller er også kompakte datastrukturer med ikke noe overhead per element, men det kan være noe ekstra data tilknyttet tabellen i sin helhet i enkelte programmeringsspråk. Noen ganger kan man oppleve at størrelsen på en tabell er mindre enn det summen av størrelse til elementene hadde vært om objektene ikke var del av en tabell. Dette fordi flere objekter kan lagres i det samme ordet når de er elementer i en tabell, mens de ellers blir tildelt ett ord hver.
Bruksområder[rediger | rediger kilde]
Tabeller blir brukt til å implementere vektorer og matriser, samt tabeller i hverdagslig forstand.
På grunn av sin ytelse blir tabeller ofte brukt til å implementere andre datastrukturer, slik som heaper, hashtabeller, køer, stakker og strenger.
Vanligvis kan hele dataminnet ses på som én stor tabell av byte eller ord. Et program kan tilsvarende allokere én eller flere store tabeller fra operativsystemet og selv allokere ytterligere minne den trenger fra disse tabellene.
Indeksering[rediger | rediger kilde]
En avgrenset mengde med heltall utgjør de gyldige indeksene til en tabell. I noen tilfeller blir indeksene sjekket for gyldighet før de benyttes, mens det i andre tilfeller er opp til programmereren å ikke bruke ugyldige indekser. Bruk av ugyldige indekser fører til udefinert oppførsel fra programmets side.
Indeksen til det første elementet varierer fra programmeringsspråk til programmeringsspråk. Stort sett har man tre kategorier: første indeks er 0, første indeks er 1, eller så kan første indeks være hva nå enn programmereren vil at den skal være.
Null-basert indeksering anses som den mest naturlige og har sitt opphav i maskinkode. Denne indekseringsmåten ble utbredt med programmeringsspråket C, som er et veldig maskinnært programmeringsspråk. Indeksen i en én-dimensjonal tabell er dermed en offset fra adressen til det første (nulte) elementet.
Én-basert indeksering har sitt opphav i tradisjonell matematikk, hvor indeksen 1 står får det første elementet. n-basert indeksering gjør det mulig for programmereren å velge den nedre grensen for gyldige indekser som passer best for problemet som skal løses.
Hvordan siste gyldige indeks defineres varierer også fra programmeringsspråk til programmeringsspråk. Ved opprettelse av en tabell angir man i noen språk størrelsen på tabellen og siste gyldige indeks beregnes ut fra det. I andre programmeringsspråk er det motsatt.
Flerdimensjonale tabeller[rediger | rediger kilde]
Vanlige tabeller indekseres med ett enkelt heltall og kalles derfor én-dimensjonale. I noen sammenhenger kan det være nyttig med tabeller med flere dimensjoner, for eksempel i numeriske applikasjoner og innen bildebehandling. I disse tilfellene vil det være nødvendig med flere indekser for å indeksere et element, slik som a[3,1,5]. Antallet indekser vil være det samme som antall dimensjoner. To-dimensjonale tabeller er egnet til å representere matriser og bilder. Tabeller med flere dimensjoner er sjeldnere.
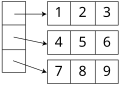
Hvordan man legger ut en én-dimensjonal tabell i minnet er ganske rett fram. Man bare plasserer alle elementene etterhverandre i minnet i den rekkefølgen de ligger i tabellen. For flerdimensjonale tabeller blir løsningen mindre åpenbar. Ta for eksempel den følgende enkle to-dimensjonale tabellen:
Her finnes følgende løsninger for hvordan elementene plasseres i minnet:
- Radvis: Man lagrer alle elementene i en rad etter hverandre, så fortsetter man man elementene på neste rad. Dette blir brukt for statiske tabeller i C.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
- Kolonnevis: Man lagrer alle elementene i en kolonne etterhverandre, så fortsetter man med elementene i neste kolonne. Dette blir brukt i Fortran.
| 1 | 4 | 7 | 2 | 5 | 8 | 3 | 6 | 9 |
- Tabeller med tabeller: Man oppretter en èn-dimensjonal tabell som inneholder referanser til andre tabeller. Disse undertabellene kan enten utgjøre rader eller kolonner.
De første to løsningene er mer kompakte og har bedre lokalitet. Ulempen er at tabellene må være rektangulære, altså at alle radene må inneholde like mange elementer. Tabeller med tabeller gjør det derimot mulig å gi hver rad eller hver kolonne ulik lengde. Dette gjør at mengden med gyldige indekser i de høyere dimensjonene avhenger av indeksene i lavere dimensjoner. Tabeller med tabeller er også den eneste mulige løsningen i programmeringsspråk uten innebygget støtte for flerdimensjonale tabeller. Dersom data i tabellform skal overføres mellom to programmer, er det viktig at begge programmene er enig hvordan flerdimensjonale tabeller legges ut i minnet.
I enkelte tilfeller kan der være nyttig å legge ut tabellelementene i den rekkefølgen de vanligvis brukes av programmet. For eksempel vil man i matrisemultiplikasjonen AB gå igjennom matrisen A rad for rad og matrisen B kolonne for kolonne. Det vil da kunne være raskest å lagre A radvist og B kolonnevist, noe en kompilator kan finne på å gjøre automatisk. Andre mer eksotiske måter å legge ut elementene i minnet finnes, for eksempel dersom man vanligvis itererer diagonalt over matrisen.