Hyperboloide
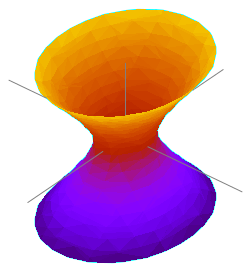

I matematikk er en hyperboloide en krum andregradsflate (kjeglesnittflate) som oppstår når en hyperbel dreies 180° om en av sine akser. Når den blir skåret av forskjellige plan, gir den ulike kjeglesnitt (ellipser, parabler eller hyperbler), avhengig av hvor skjæringen skjer. En hyperboloide har tre symmetriplan; deres skjæringspunkt kalles hyperboloidens sentrum, og de tre skjæringslinjer hyperboloidens akser.
Det finnes to typer hyperboloider: en sammenhengende enkappet hyperboloide og en som består av to atskilte deler, en tokappet hyperboloide. I et koordinatsystem der aksene sammenfaller med hyperboloidens akser, har den enkappede hyperboloiden ligningen
og den tokappede hyperboloiden har ligningen
Disse blir også kalt elliptiske hyperboloider. Det er en omdreiningshyperboloide hvis og bare hvis a = b. Den enkappede hyperboloiden er en linjeflate, ettersom den kan tenkes fremkommet ved bevegelsen av en rett linje på to forskjellige måter.
Når en hyperbel dreies om en av sine akser, oppstår en omdreiningshyperboloide (også kalt en sirkulær hyperboloide). Hvis dreiningen foregår om den akse som skjærer hyperbelen, får man en tokappet hyperboloide, mens dreining om den annen akse gir en enkappet hyperboloide.
Eksterne lenker[rediger | rediger kilde]
- (en) Hyperboloid – kategori av bilder, video eller lyd på Commons
- Artikkel på SNL


