A*
A* (uttales «A star» eller «A stjerne») er en søkealgoritme for å effektivt kunne traversere noder i grafer. Den er kjent for å være effektiv og presis og blir brukt mye innen kunstig intelligens. Den bruker en ekstensjon av Dijkstras algoritme. A* tar i bruk heuristikk som gjør den mer effektiv. Algoritmen ble først beskrevet av Peter Hart, Nils Nilsson og Bertram Raphael ved SRI International i 1968.[1]
Beskrivelse
[rediger | rediger kilde]A* bruker beste-først søk og finner stien med minst kostnad gitt en initiell node til en mål-node. A* følger stien med minst forventet total kostnad. Den holder en prioritetsliste av alternative stier og om kostnaden på den nåværende stien overstiger den første i listen kan den skifte alternativ.
Det som gjør at A* er så effektiv er det at den tar i bruk heuristikk for å finne ut hvilke av nodene i treet den bør søke gjennom først. Dette blir representert som en funksjon som er en sum av to funksjoner:
- en funksjon som er distansen fra start-noden til den nåværende noden x (vanligvis )
- en heuristikk funksjon som er en estimering av distansen fra x til målet (vanligvis ).
For at A* skal være optimal må aldri overestimere kostnaden for å nå målet. Det vil si at den er tillatelig (engelsk: admissible).
Prosess
[rediger | rediger kilde]Det første algoritmen gjør er å søke gjennom de stiene som mest sannsynlig leder til målet. Det som skiller A* fra beste-først-søk og andre grådige algoritmer er at den tar hensyn til distansen den allerede har dekket (g(x)).
Den starter med den første noden, og opprettholder en kø av noder som skal besøkes. Nodene er sortert etter verdien av , den som har lavest verdi er først i køen. I hvert steg av algoritmen vil noden med lavest verdi fjernes fra køen og og verdiene til naboene til noden vil bli oppdatert og lagt til i køen. Dette fortsetter helt til en mål-node har lavest verdi i køen, eller til køen er tom (ingen løsning finnes). Mål-noder kan bli passerte flere ganger i algoritmen men siden det finnes andre stier med lavere verdi stopper ikke algoritmen før den finner den korteste veien.
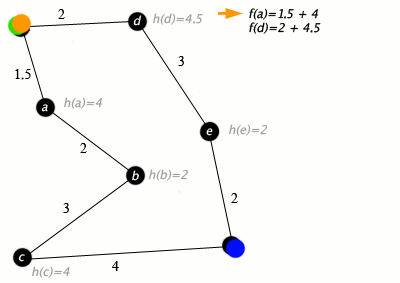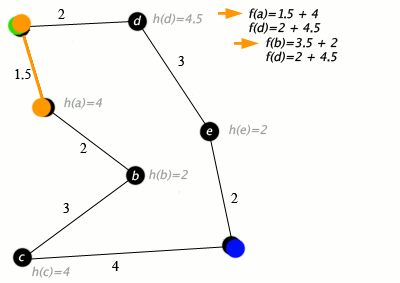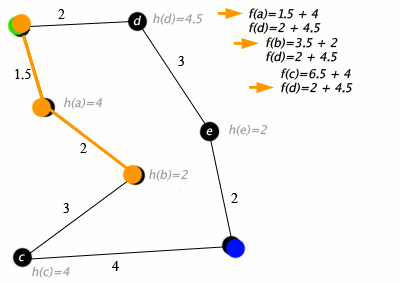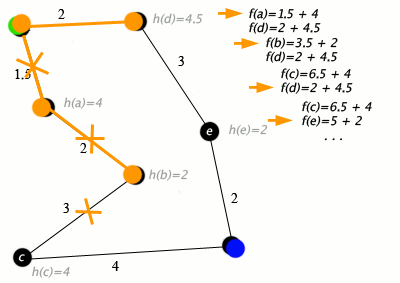
Eksempel
[rediger | rediger kilde]
Ett eksempel der en A* algoritme søker gjennom en graf av byer(noder) koblet sammen av veier(kanter). Dette eksempelet bruker distansen i en rett linje(tenk fly) fra node til mål-node som heuristikk.
Egenskaper
[rediger | rediger kilde]I likhet med bredde-først-søk er A* komplett og vil alltid finne en løsning om den finnes.
Om heuristikk funksjonen er tillatelig (at den aldri overestimerer), er A* selv tillatelig og optimal såvidt at vi ikke bruker et lukket sett.
A* er også optimalt effektiv for hvilken som helst heuristikk . Dette betyr at ingen annen algoritme som tar i bruk samme heuristikk vil besøke færre noder enn A*.
Kompleksitet
[rediger | rediger kilde]Tids-kompleksiteten til A* er avhengig av heuristikk funksjonen. I verste scenario er antallet noder besøkt eksponentiell i vekst i forhold til lengden av løsningen: der er forgreinings-faktoren (gjennomsnittet av ut-kanter per node). Dette forutsetter at det finnes en løsning.